题目链接：Dashboard - Codeforces Round 1007 (Div. 2) - Codeforces
A. The Play Never Ends
思路
可以发现根据题意来，进行的比赛是有规律的
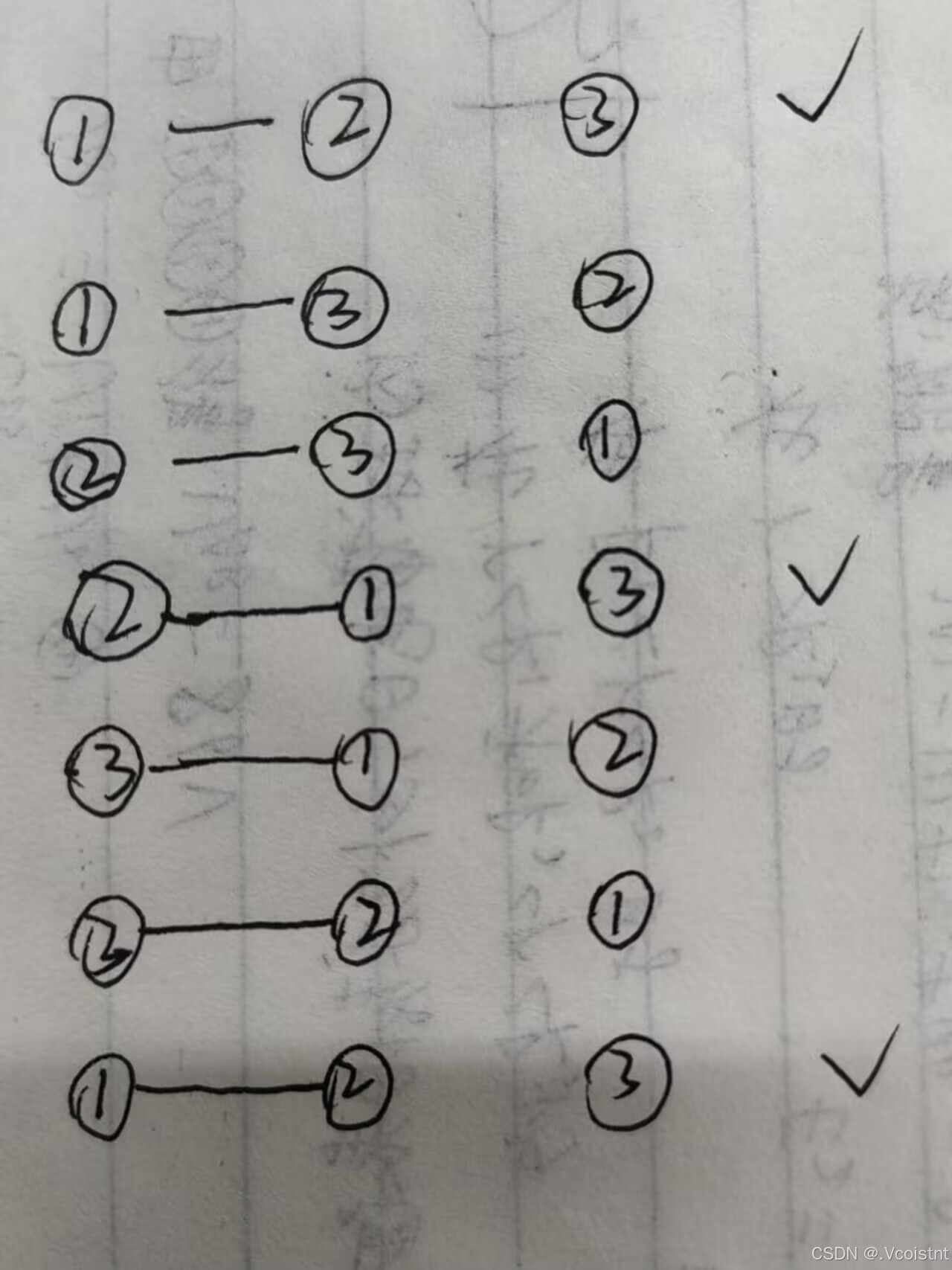只有当1，4，7.....的时候第1场的观众才能再次成为观众
代码
void solve(){int k;cin>>k;if((k-1)%3){cout<<"NO\n";}else{cout<<"YES\n";}
}B. Perfecto
思路
赛时也是想了四种构造方法但是
因为这样写全wa2了（给我改破防了）
这里给出两种简单易想的构造
首先可以发现如果所有数的累加和是完全平方数那么这个n肯定是不可以的直接特判输出-1
第一种是完全贪心的，如果从1~n当前累加和是完全平方数，那么我们把i与i+1互换，这样累加和x变成x+1之后就不是完全平方数了，可以证明此是可行的
第二种就是直接构造成 2 1 3 5 6 7...n 4 这样也是可行的，可以打表进行证明
代码
void solve(){int n;cin>>n;int t=(n+1)*n/2;int x=sqrt(t);if(x*x==t){cout<<"-1\n";return;}vi a(n+10);for(int i=1;i<=n;i++) a[i]=i;int sum=0;for(int i=1;i<=n;i++){int st=sum+a[i];int tt=sqrt(st);if(tt*tt==st){swap(a[i],a[i+1]);}sum+=a[i];}for(int i=1;i<=n;i++){cout<<a[i]<<" ";}cout<<"\n";
}void solve(){int n;cin>>n;int t=(n+1)*n/2;int x=sqrt(t);if(x*x==t){cout<<"-1\n";return;}if(n==2){cout<<"2 1\n";return;}if(n==3){cout<<"2 1 3\n";return;}cout<<"2 1 3 ";for(int i=5;i<=n;i++){cout<<i<<" ";}cout<<"4";cout<<"\n";
}C. Trapmigiano Reggiano
思路
此题你要观察出一个结论，假设x节点为树根，逐渐遍历深度从最深~1的节点，那么最终小鼠便会到达x节点。
为什么呢？因为，当小鼠位于任意位置时，你把深度为n的节点遍历完之后，小鼠停留的位置所在的深度最深只能是n，同理当你遍历完n-1深度的节点时，小鼠所在的深度要<=n-1，那么依次推当遍历完深度为1的时候小鼠只能位于x节点；
那么此题我们便以ed为根节点，遍历输出即可
代码
#include<bits/stdc++.h>
using namespace std;#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;void solve(){int n,s,e;cin>>n>>s>>e;vector<vi> g(n+10);for(int i=1;i<n;i++){int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}vector<vi> dis(n+10);vi d(n+10);auto dfs=[&](auto self,int v,int fa)->void{d[v]=d[fa]+1;dis[d[v]].push_back(v);for(int u:g[v]){if(u==fa) continue;self(self,u,v);}};dfs(dfs,e,0);for(int i=n;i>=1;i--){for(int j:dis[i]){cout<<j<<" ";}}cout<<"\n";
}
signed main() {vcoistntcout<<fixed<<setprecision(2);int _=1;cin>>_;while(_--) solve();return 0;
}D1. Infinite Sequence (Easy Version)
思路
此题与数学公式推导和按位异或的性质有关
初始将n变为奇数，便于后面异或性质的抵消，如果不是奇数根据题目补上一个数
用数组表示前缀异或和，用
假设我们要求的值，可以发现一下几种情况，
如果，便可直接求出:
此时
；
此时
如果，则
根据n为奇数并且按位异或的性质其中就能够抵消掉
因此 （
为奇数时）
（
为偶数时）
那么就可以不断往下寻找直到 m<=2*n 时
复杂度为
代码
#include<bits/stdc++.h>
using namespace std;#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;void solve(){int n,l,r;cin>>n>>l>>r;vi pre(2*n+10);vi a(2*n+10);for(int i=1;i<=n;i++){cin>>a[i];pre[i]=pre[i-1]^a[i];}if(n%2==0){n++;a[n]=pre[n/2];pre[n]=pre[n-1]^a[n];}int p=pre[n];for(int i=n+1;i<=2*n;i++){a[i]=pre[i/2];pre[i]=pre[i-1]^a[i];}int m=l;int res=0;while(1){if(m<=2*n){res^=a[m];break;}res^=p;if((m/2-n)%2==0){break;}m/=2;}cout<<res<<"\n";
}
signed main() {vcoistntcout<<fixed<<setprecision(2);int _=1;cin>>_;while(_--) solve();return 0;
}
