《数值计算方法》丁丽娟-数值实验作业-第六章(MATLAB)
作业P203: 1, 2, 4, 6, 7, 10, 12, 13(1)
数值实验P205: 2
代码+手写计算:函数逼近算法 - 最小二乘法拟合函数、线性最小二乘法的一般形式
数值实验作业(第六章)
代码仓库:https://github.com/sylvanding/bit-numerical-analysis-hw 点个star⭐️吧~
P205. Q2
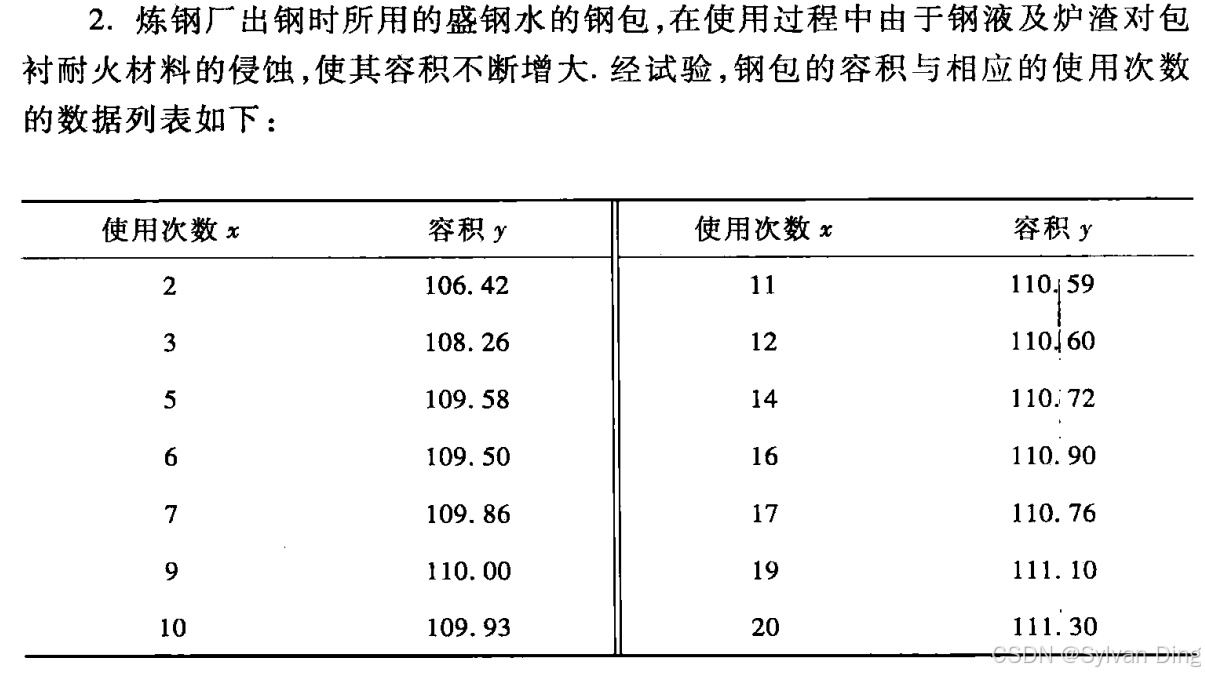
实验内容、步骤及结果
chap-6\leastSquaresMatrix.m:
function [A, b] = leastSquaresMatrix(x, y, m)assert(length(x) == length(y), 'The lengths of x and y must be the same.');n = length(x);A = zeros(m + 1, m + 1);b = zeros(m + 1, 1);for i = 1:m + 1for j = 1:m + 1for k = 1:nA(i, j) = A(i, j) + x(k) ^ (i - 1 + j - 1);endendfor k = 1:nb(i) = b(i) + y(k) * x(k) ^ (i - 1);endendend
chap-6\P205_Q2.m:
x = [2; 3; 5; 6; 7; 9; 10; 11; 12; 14; 16; 17; 19; 20];
y = [106.42; 108.26; 109.58; 109.50; 109.86; 110.00; 109.93; 110.59; 110.60; 110.72; 110.90; 110.76; 111.10; 111.30];
m = 1;[A, b] = leastSquaresMatrix(1 ./ x, 1 ./ y, m);coefficients = A \ b;disp('y = x / ax + b');
disp('1/y = a + b/x');disp('Coefficients:');
disp(coefficients);a = coefficients(1);
b = coefficients(2);% Plot the original data points
figure;
scatter(x, y, 'filled');
hold on;% Plot the fitted line
x_fit = linspace(min(x), max(x), 100);
y_fit = x_fit ./ (a * x_fit + b);
plot(x_fit, y_fit, 'r');xlabel('x');
ylabel('y');
title('Data points and fitted line');
legend('Data points', 'Fitted line');
hold off;
>> P205_Q2
y = x / ax + b
1/y = a + b/x
Coefficients:0.00900.0008
实验结果分析
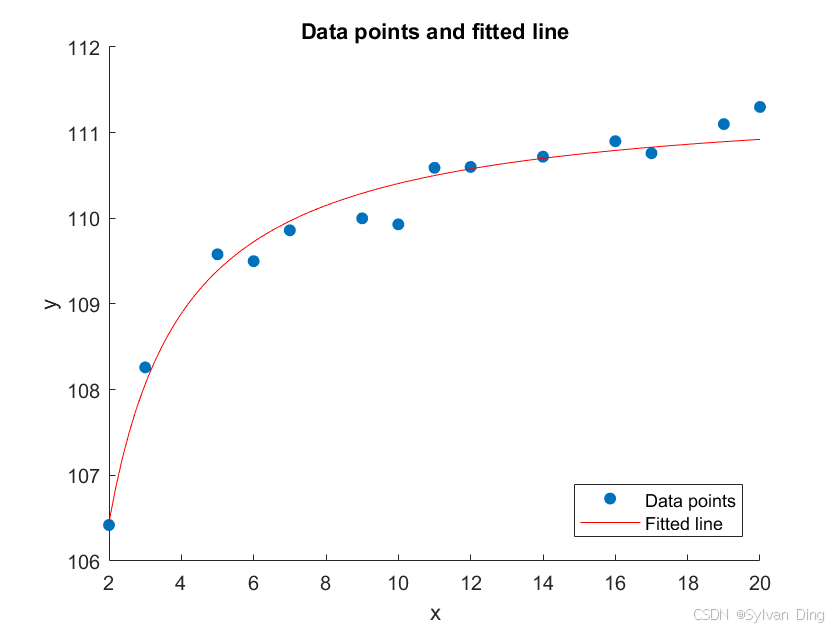
用最小二乘求出的拟合函数(red line)较好地拟合在了数据点(blue points)的附近。
补充代码
chap-6\leastSquaresMatrix_Func.m
function [A, b] = leastSquaresMatrix_Func(H, g, int_a, int_b)% Number of basis functionsn = length(H);% Initialize A and bA = zeros(n, n);b = zeros(n, 1);% Compute matrix Afor i = 1:nfor j = 1:nA(i, j) = integral(@(x) H{i}(x) .* H{j}(x), int_a, int_b, 'ArrayValued', true);endend% Compute vector bfor i = 1:nb(i) = integral(@(x) H{i}(x) .* g(x), int_a, int_b, 'ArrayValued', true);endend
chap-6\P203_Q1.m
x = [1.36; 1.49; 1.73; 1.81; 1.95; 2.16; 2.28; 2.48];
y = [14.094; 15.069; 16.844; 17.378; 18.435; 19.949; 20.963; 22.495];
m = 1;[A, b] = leastSquaresMatrix(x, y, m);coefficients = A \ b;disp('x:');
disp(x);disp('y:');
disp(y);disp('m:');
disp(m);disp('A:');
disp(A);disp('b:');
disp(b);disp('Coefficients:');
disp(coefficients);
chap-6\P203_Q2.m
x = [1; 3; 4; 5; 6; 7; 8; 9; 10];
y = [10; 5; 4; 2; 1; 1; 2; 3; 4];
m = 2;[A, b] = leastSquaresMatrix(x, y, m);coefficients = A \ b;disp('x:');
disp(x);disp('y:');
disp(y);disp('m:');
disp(m);disp('A:');
disp(A);disp('b:');
disp(b);disp('Coefficients:');
disp(coefficients);
chap-6\P203_Q4.m
x = [19; 25; 31; 38; 44];
y = [19.0; 32.3; 49.0; 73.3; 97.8];
m = 1;[A, b] = leastSquaresMatrix(x .^ 2, y, m);coefficients = A \ b;disp('y = a + bx^2');disp('x:');
disp(x);disp('y:');
disp(y);disp('m:');
disp(m);disp('A:');
disp(A);disp('b:');
disp(b);disp('Coefficients:');
disp(coefficients);
chap-6\P203_Q6.m
x = [1; 2; 3; 4; 5; 6; 7; 8];
y = [15.3; 20.5; 27.4; 36.6; 49.1; 65.6; 87.87; 117.6];
m = 1;[A, b] = leastSquaresMatrix(x, log(y), m);coefficients = A \ b;disp('y = a*exp(bx)');
disp('ln(y) = ln(a) + bx');disp('x:');
disp(x);disp('y:');
disp(y);disp('log(y)');
disp(log(y));disp('m:');
disp(m);disp('A:');
disp(A);disp('b:');
disp(b);disp('Coefficients:');
disp(coefficients);a = exp(coefficients(1));
b = coefficients(2);disp('a:');
disp(a);disp('b:');
disp(b);
chap-6\P203_Q7.m
x = [1; 2; 3; 4; 6; 8; 10; 12; 14; 16];
y = [4.00; 6.41; 8.01; 8.79; 9.53; 9.86; 10.33; 10.42; 10.53; 10.61];
m = 1;[A, b] = leastSquaresMatrix(1 ./ x, 1 ./ y, m);coefficients = A \ b;disp('y = x / ax + b');
disp('1/y = a + b/x');disp('x:');
disp(x);disp('y:');
disp(y);disp('1/x');
disp(1 ./ x);disp('1/y');
disp(1 ./ y);disp('m:');
disp(m);disp('A:');
disp(A);disp('b:');
disp(b);disp('Coefficients:');
disp(coefficients);
chap-6\P203_Q12.m
% Define basis functions
H = {@(x) 1, @(x) x .^ 2, @(x) x .^ 4};% Define target function
g = @(x) cos(x);% Define integration interval
int_a = -pi / 2;
int_b = pi / 2;[A, b] = leastSquaresMatrix_Func(H, g, int_a, int_b);coefficients = A \ b;disp('A:');
disp(A);disp('b:');
disp(b);disp('Coefficients:');
disp(coefficients);
P203_outputs.txt
>> P203_Q1
x:1.36001.49001.73001.81001.95002.16002.28002.4800y:14.094015.069016.844017.378018.435019.949020.963022.4950m:1A:8.0000 15.260015.2600 30.1556b:145.2270284.8363Coefficients:3.91617.4639>> P203_Q2
x:1345678910y:1054211234m:2A:9 53 38153 381 3017381 3017 25317b:321471025Coefficients:13.4597-3.60530.2676>> P203_Q4
y = a + bx^2
x:1925313844y:19.000032.300049.000073.300097.8000m:1A:5 53275327 7277699b:1.0e+05 *0.00273.6932Coefficients:0.97260.0500>> P203_Q6
y = a*exp(bx)
ln(y) = ln(a) + bx
x:12345678y:15.300020.500027.400036.600049.100065.600087.8700117.6000log(y)2.72793.02043.31053.60003.89394.18364.47594.7673m:1A:8 3636 204b:29.9795147.1406Coefficients:2.43670.2913a:11.4358b:0.2913>> P203_Q7
y = x / ax + b
1/y = a + b/x
x:12346810121416y:4.00006.41008.01008.79009.53009.860010.330010.420010.530010.61001/x1.00000.50000.33330.25000.16670.12500.10000.08330.07140.06251/y0.25000.15600.12480.11380.10490.10140.09680.09600.09500.0943m:1A:10.0000 2.69232.6923 1.4930b:1.23300.4586Coefficients:0.07890.1649>> P203_Q12
A:3.1416 2.5839 3.82522.5839 3.8252 6.74173.8252 6.7417 12.9380b:2.00000.93480.9585Coefficients:0.9996-0.49640.0372
手写部分(含证明)


















