SVM(支持向量机)
支持向量机(Support Vector Machine,SVM)是一种用于分类和回归分析的监督学习模型,在机器学习领域中被广泛应用。SVM的目标是找到一个最佳的分割超平面,将不同类别的数据分开,使得两个类别之间的间隔(即边界)最大化。下面是对SVM的详细解释:
SVM的基本概念
-
超平面(Hyperplane):
-
在二维空间中,超平面是将平面分为两部分的直线
-
在三维空间中,超平面是将空间分为两部分的平面
-
在更高维度的空间中,超平面是将该空间分为两部分的一个n-1维的子空间
-
-
支持向量(Support Vectors):
-
支持向量是离分割超平面最近的那些数据点
-
这些点是最重要的,因为它们定义了超平面的位置和方向
-
移动这些点将会改变超平面的位置
-
-
间隔(Margin):
-
间隔是指支持向量与超平面之间的距离
-
SVM的目标是最大化这个间隔,以提高分类器的鲁棒性和泛化能力
-
SVM的核函数(Kernel Function)
SVM可以通过使用核函数将输入数据映射到高维空间,在高维空间中,原本非线性可分的数据可以变成线性可分的。常见的核函数包括:
-
线性核(Linear Kernel):适用于线性可分的数据。
-
多项式核(Polynomial Kernel):用于非线性数据。
-
径向基函数核(RBF Kernel):也称高斯核,常用于非线性数据。
-
Sigmoid核(Sigmoid Kernel):模拟神经网络的激活函数。
SVM算法工作原理
-
训练阶段:
-
给定训练数据集,SVM通过求解一个优化问题,找到最大化间隔的分割超平面。
-
该优化问题通常是一个凸二次规划问题,可以通过各种优化算法求解。
-
-
分类阶段:
-
对于新的数据点,SVM根据其与分割超平面的相对位置进行分类。
-
数据点落在超平面一侧的属于一个类别,落在另一侧的属于另一个类别。
-
SVM的数学描述
假设我们有一个训练数据集 ( (x_1, y_1), (x_2, y_2), ···, (x_n, y_n) ),其中 ( x_i ) 是特征向量,( y_i ) 是对应的类别标签,取值为 ( {+1, -1} )。
SVM的优化目标是:
其中,( w ) 是超平面的法向量,( b ) 是偏置项。
SVM的优缺点
优点:
-
能够有效处理高维空间的数据。
-
在样本数量远大于特征数量的情况下仍然有效。
-
具有较好的泛化能力,能够防止过拟合。
缺点:
-
对于大规模数据集,训练时间较长。
-
对于含有噪声的数据表现较差,尤其是在类别重叠的情况下。
-
SVM的参数选择和核函数的选择需要经验和实验。
示例代码1
使用Python的scikit-learn库实现SVM分类器进行二维点的分类。
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import classification_report, accuracy_score
import matplotlib.pyplot as plt# 加载Iris数据集
iris = datasets.load_iris()
X = iris.data[:, :2] # 仅使用前两个特征进行可视化
y = iris.target# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)# 创建和训练SVM分类器
clf = SVC(kernel='linear', C=1.0)
clf.fit(X_train, y_train)# 预测测试集
y_pred = clf.predict(X_test)# 计算准确率和分类报告
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
print(classification_report(y_test, y_pred))# 可视化决策边界
def plot_decision_boundary(clf, X, y):h = .02 # 网格步长x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.8)plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')plt.xlabel('Sepal length')plt.ylabel('Sepal width')plt.title('SVM Decision Boundary')plt.show()plot_decision_boundary(clf, X_test, y_test)
结果可视化:

上图中有部分点被错误的分类了,分类错误可能由以下原因引起:数据中存在噪声和异常值、数据本身在当前维度下不可分、训练数据量不足或特征选择不当、模型参数设置不合理、类别不平衡问题、以及模型过拟合或欠拟合。这些因素都会影响模型的准确性和泛化能力,导致在某些数据点上出现分类错误。
示例代码2
使用SVM进行三维数据分割。
import numpy as np
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 在Jupyter Notebook中启用交互模式
%matplotlib notebook# 生成合成数据集
np.random.seed(42)
X, y = datasets.make_classification(n_samples=100, n_features=3, n_informative=3, n_redundant=0, n_clusters_per_class=1
)# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)# 创建和训练SVM分类器
clf = SVC(kernel='linear', C=1.0)
clf.fit(X_train, y_train)# 预测测试集
y_pred = clf.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')# 可视化决策边界
def plot_decision_boundary_3d(clf, X, y):fig = plt.figure()ax = fig.add_subplot(111, projection='3d')# 设置网格范围x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1z_min, z_max = X[:, 2].min() - 1, X[:, 2].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))# 计算平面上的决策函数值zz = (-clf.intercept_[0] - clf.coef_[0][0] * xx - clf.coef_[0][1] * yy) / clf.coef_[0][2]# 绘制决策平面ax.plot_surface(xx, yy, zz, alpha=0.3, color='r', edgecolor='none')# 绘制数据点scatter = ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.viridis, edgecolors='k')legend1 = ax.legend(*scatter.legend_elements(), title="Classes")ax.add_artist(legend1)ax.set_xlabel('Feature 1')ax.set_ylabel('Feature 2')ax.set_zlabel('Feature 3')ax.set_title('SVM Decision Boundary in 3D')# 允许图形旋转ax.view_init(elev=30, azim=30)plt.show()plot_decision_boundary_3d(clf, X_test, y_test)结果可视化:
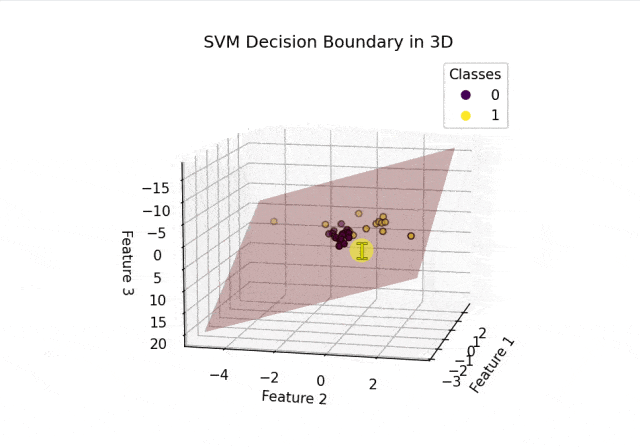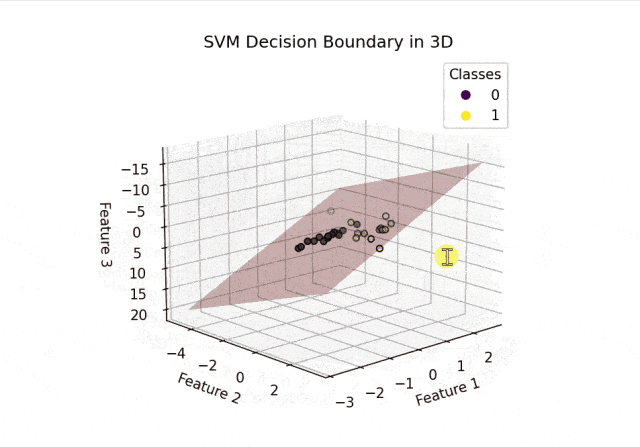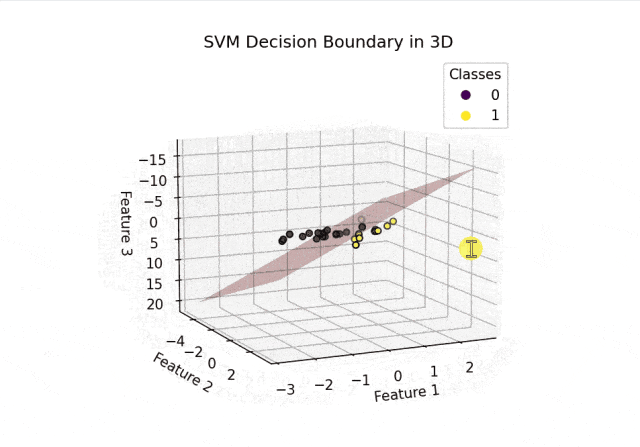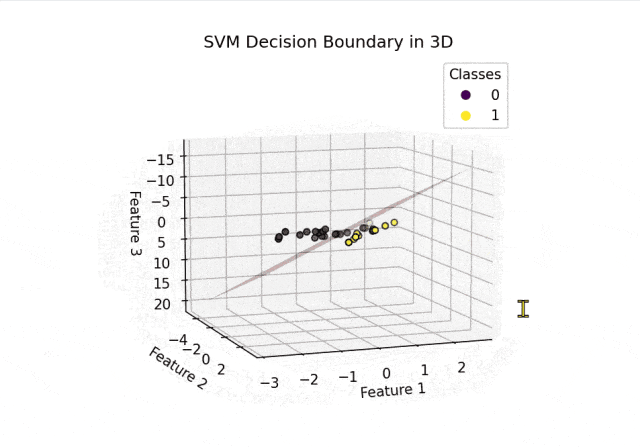
从上面的结果可以看出SVM正确分割了两类空间中的点。以上内容总结自网络,如有帮助欢迎转发,我们下次再见!














