参考资料:代码随想录
300.最长递增子序列
力扣题目链接(opens new window)
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
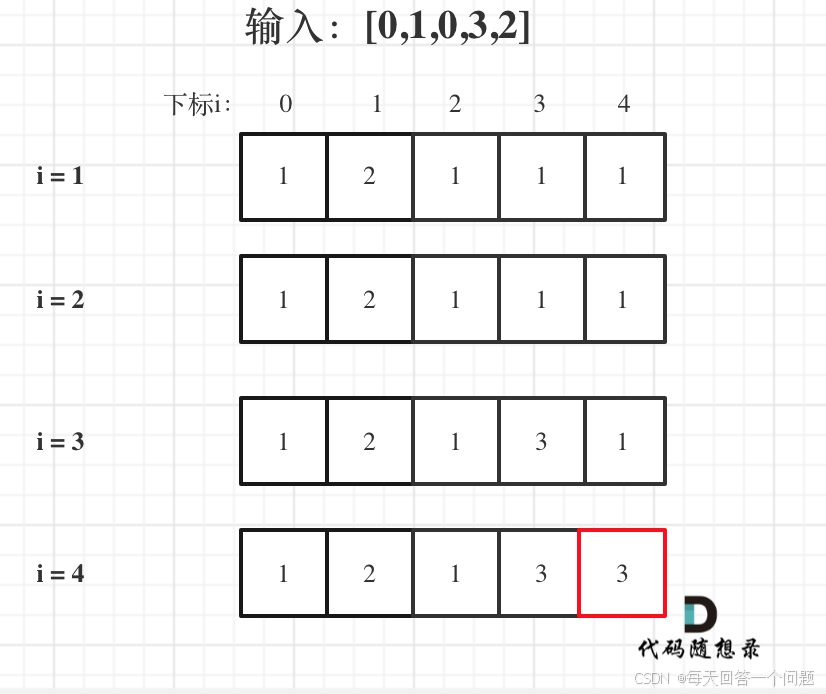
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
提示:
1 <= nums.length <= 2500
-10^4 <= nums[i] <= 104
思路分析
开始还是使用动规5步曲取分析
- dp[i]的定义
- dp[i]表示nums[i]结尾的最长递增子序列的长度
- 补充 i之前包括i的 以nums[i[结尾的
- 如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾
- 状态转移方程式
- if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
- dp[i]的初始化
- 每一个i对应的dp[i] ,起始大小都至少是1.
- 确定遍历顺序
- 从前向后遍历
- 因为dp[i] 是由0到i-1各个位置的最长递增子序列 推导
- 推导dp数组
代码实现
class Solution {
public:int lengthOfLIS(vector<int>& nums) {// 如果数组长度小于等于1,直接返回数组长度,因为最长递增子序列就是它本身if (nums.size() <= 1) return nums.size();// 定义一个动态规划数组 dp,dp[i] 表示以 nums[i] 结尾的最长递增子序列的长度// 初始值为 1,因为每个元素至少可以单独成为一个子序列vector<int> dp(nums.size(), 1);// 用于记录最终的结果,即整个数组的最长递增子序列的长度int result = 0;// 遍历数组中的每一个元素 i(从第 1 个元素开始)for (int i = 1; i < nums.size(); i++) {// 对于每个 i,遍历其前面的所有元素 j(从 0 到 i-1)for (int j = 0; j < i; j++) {// 如果当前元素 nums[i] 大于 nums[j],说明可以将 nums[i] 接在 nums[j] 后面形成更长的递增子序列if (nums[i] > nums[j]) {// 更新 dp[i] 的值,取 dp[i] 和 dp[j] + 1 中的较大值dp[i] = max(dp[i], dp[j] + 1);}}// 每次更新完 dp[i] 后,检查是否需要更新结果 result// result 始终记录所有 dp[i] 中的最大值if (dp[i] > result) result = dp[i];}// 返回最终结果,即最长递增子序列的长度return result;}
};
674. 最长连续递增序列
力扣题目链接(opens new window)
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。
提示:
0 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9
思路分析
class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {// 如果数组为空,则直接返回0,因为空数组没有递增子序列if(nums.size() == 0) return 0;// 初始化结果变量 result,用于记录最长连续递增子序列的长度int result = 1;// 定义一个动态规划数组 dp,初始值为1,表示每个元素本身至少是一个长度为1的递增子序列vector<int> dp(nums.size(), 1);// 遍历数组,从第二个元素开始(i = 1)for(int i = 1; i < nums.size(); i++) { // 如果当前元素大于前一个元素,说明可以延续递增子序列if(nums[i] > nums[i - 1]) { // 当前 dp[i] 的值等于前一个 dp[i-1] 的值加1dp[i] = dp[i - 1] + 1;}// 更新结果 result,确保它始终保存当前找到的最长递增子序列长度if(dp[i] > result) result = dp[i];}// 返回最终的结果return result;}
};
718. 最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
思路分析
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {// 定义一个二维动态规划数组 dp,大小为 (nums1.size() + 1) x (nums2.size() + 1)// dp[i][j] 表示以 nums1 的前 i 个元素和 nums2 的前 j 个元素结尾的最长公共子数组的长度vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));// 初始化结果变量 result,用于记录最长公共子数组的长度int result = 0;// 遍历 nums1 和 nums2 的所有元素for (int i = 1; i <= nums1.size(); i++) { for (int j = 1; j <= nums2.size(); j++) { // 如果 nums1 的第 i-1 个元素等于 nums2 的第 j-1 个元素if (nums1[i - 1] == nums2[j - 1]) { // 当前 dp[i][j] 的值等于左上角 dp[i-1][j-1] 的值加1// 这是因为当前匹配的元素延续了之前的公共子数组dp[i][j] = dp[i - 1][j - 1] + 1;}// 更新结果 result,确保它始终保存当前找到的最长公共子数组的长度if (dp[i][j] > result) result = dp[i][j];}}// 返回最终的结果return result;}
};
这里是每天回答一个问题
如果觉得对你有帮助的话
麻烦点一个免费的赞