河北建站公司_京津冀协同发展存在的突出问题_my63777免费域名查询2023年_网站seo需要用到哪些工具

本文提出了一种新的jSO变体APSM-jSO，通过简单有效的修改来提高其性能。APSM-jSO和jSO之间有三个主要区别。首先，设计了一种新的自适应选择机制（APSM）来从历史记忆中选择条目，以充分利用历史记忆中更好的条目。随后，利用先进先出（FIFO）方法更新外部档案，以保持人口多样性，避免过度使用外部档案。最后，采用基于秩的选择压力（RSP）的新突变策略来增强APSM-jSO的开发。文章于2023发表在中科院1区顶刊Swarm and Evolutionary Computation上。

2. 差分进化算法变体简介

2.1. 差分进化

经典差分进化（DE）[1] 是一种基于种群的进化算法，其中三个操作：变异、交叉和选择操作，在进化过程中执行。

初始种群 $P$ 使用均匀分布生成，如公式(1)所示。
$$x_i^j=L^j+\text{rand}\cdot (U^j-L^j)\text{\hspace{1em}(1)}$$
其中 $\text{rand}\in (0,1)$ 是均匀分布的随机数， i ∈ { 1 , 2 , 3 , ⋯ , N P } i \in \{1, 2, 3, \cdots, NP\} i∈{1,2,3,⋯,NP} 是个体索引，$NP$ 是种群大小， j ∈ { 1 , 2 , 3 , ⋯ , D } j \in \{1, 2, 3, \cdots, D\} j∈{1,2,3,⋯,D} 是维度索引，$D$ 是维度，$L^j$ 和 $U^j$ 是问题特定的第 $j$ 维的下界和上界[11]。

DE中生成变异向量 $v_i$ 的四种广泛使用的经典的变异策略，DE/best/2、DE/rand/2 和 DE/current-to-best/1、DE/current-to-rand/1，描述如下(2)、(3)、(4)、(5)。

$$v_i=x_{\text{best}}+F\cdot (x_{r_1}-x_{r_2})+F\cdot (x_{r_3}-x_{r_4})\text{\hspace{1em}(2)}$$
$$v_i=x_{r_1}+F\cdot (x_{r_2}-x_{r_3})+F\cdot (x_{r_4}-x_{r_5})\text{\hspace{1em}(3)}$$
$$v_i=x_i+F\cdot (x_{\text{best}}-x_i)+F\cdot (x_{r_1}-x_{r_2})\text{\hspace{1em}(4)}$$
$$v_i=x_i+K\cdot (x_{r_1}-x_i)+F\cdot (x_{r_2}-x_{r_3})\text{\hspace{1em}(5)}$$

其中 r 1 , r 2 , r 3 , r 4 , r 5 ∈ { 1 , 2 , 3 , ⋯ , N P } r_1, r_2, r_3, r_4, r_5 \in \{1, 2, 3, \cdots, NP\} r1​,r2​,r3​,r4​,r5​∈{1,2,3,⋯,NP} 是均匀分布的随机索引，彼此不同。$F$ 是缩放因子，$x_{\text{best}}$ 是到目前为止获得的最佳个体。此外，当 $v_i$ 超出下界或上界时，采用修正策略，如公式(6)所示。

$$v_i^j=\{\begin{array}{ll}(L^j+x_i^j)/2,& v_i^j<L^j\\ (U^j+x_i^j)/2,& v_i^j>U^j\end{array}\text{\hspace{1em}(6)}$$

采用二项式交叉操作生成试验向量 $u_i$，基于变异向量，如公式(7)所示。

$$u_i^j=\{\begin{array}{ll}{v}_i^j,& \text{rand}<CR\text{ 或 }j=j_{\text{rand}}\\ x_i^j,& \text{否则}\end{array}\text{\hspace{1em}(7)}$$

其中 j rand ∈ { 1 , 2 , 3 , ⋯ , D } j_{\text{rand}} \in \{1, 2, 3, \cdots, D\} jrand​∈{1,2,3,⋯,D} 表示均匀随机索引，$CR$ 是交叉率。

基于贪婪策略的选择操作用于更新种群，如公式(8)所示。

$$x_i=\{\begin{array}{ll}{u}_i,& f(u_i)\le f(x_i)\\ x_i,& \text{否则}\end{array}\text{\hspace{1em}(8)}$$

其中 $f(\cdot )$ 表示特定问题的适应度函数。

2.2. SHADE[2]

SHADE 于2013年提出，采用外部存档方案和基于历史的参数调整方案。外部存档 $A$ 被引入DE以丰富种群多样性。如果试验向量 $u_i$ 优于其目标向量 $x_i$，则将其保存在外部存档中。否则，它将在下一代中保留，如公式(8)所示。一旦存档的大小 $|A|$ 达到预定大小，随机丢弃一个个体以为新插入的个体腾出空间。

基于历史的参数调整方案用于调整 $F_i$ 和 $C{R}_i$。所有成功的 $F_i$ 和 $C{R}_i$ 保存到 $S_{CR}$ 和 $S_F$ 中以更新历史记忆 $M_{CR}$ 和 $M_F$，使用加权勒梅尔平均值，如公式(9)、(10)、(11)、(12)所示。$k$ 从1开始，每代递增1。此外，如果超过内存大小 $H$ [13]，则 $k$ 重置为1。在一代中，如果所有试验向量都比相应的目标向量差，则 $M_{CR}$ 和 $M_F$ 不更新。

$$M_{F,k}=\{\begin{array}{ll}{M}_{F,k},& S_F=\varnothing \\ {\text{mean}}_{WL}(S_F),& \text{否则}\end{array}\text{\hspace{1em}(9)}$$
$$M_{CR,k}=\{\begin{array}{ll}{M}_{CR,k},& S_{CR}=\varnothing \\ {\text{mean}}_{WL}(S_{CR}),& \text{否则}\end{array}\text{\hspace{1em}(10)}$$
$${\text{mean}}_{WL}(S)=\frac{{\sum }_{n=1}^{|S|}{\omega }_n\cdot S_n^2}{{\sum }_{n=1}^{|S|}{\omega }_n\cdot S_n}\text{\hspace{1em}(11)}$$
$${\omega }_n=\frac{|f(u_n)-f(x_n)|}{{\sum }_{n=1}^{|S|}|f(u_n)-f(x_n)|}\text{\hspace{1em}(12)}$$

在公式(11)中，$S$ 表示 $S_{CR}$ 或 $S_F$。$F_i$ 和 $C{R}_i$ 对于个体 $x_i$ 通过从柯西分布（如公式(13)所示）和正态分布（如公式(15)所示）中采样创建。$F_i$ 和 $C{R}_i$ 进一步使用公式(14)和公式(16)进行修正。

$$F_i=\text{randc}(M_{F,R_i},0.1)\text{\hspace{1em}(13)}$$
$$F_i=\{\begin{array}{ll}1,& F_i>1\\ \text{应用公式(13)，}{F}_i\le 0& \end{array}\text{\hspace{1em}(14)}$$
$$C{R}_i=\text{randn}(M_{CR,R_i},0.1)\text{\hspace{1em}(15)}$$
$$C{R}_i=\{\begin{array}{l}1,C{R}_i>1\\ 0,C{R}_i<0\end{array}\text{\hspace{1em}(16)}$$

其中 R i ∈ { 1 , 2 , 3 , ⋯ , H } R_i \in \{1, 2, 3, \cdots, H\} Ri​∈{1,2,3,⋯,H} 表示随机索引。此外，使用外部存档的变异策略“DE/current-to-pbest/1”在SHADE中生成变异向量 $v_i$，如公式(17)所示。

$$v_i=x_i+F_i\cdot (x_{\text{pbest}}-x_i)+F_i\cdot (x_{r_1}-{\tilde{x}}_{r_0})\text{\hspace{1em}(17)}$$

其中 $x_{\text{pbest}}$ 表示从包括前 $NP\times p$ 个个体的主导种群中随机选择的个体，$p$ 表示贪婪因子。${\tilde{x}}_{r_0}$ 是从 $A$ 和 $P$ 的组合中选择的随机个体，与 $x_i$、$x_{\text{pbest}}$ 或 $x_{r_1}$ 不同。

由于个体的交叉率不同，公式(7)已被修改为公式(18)。

$$u_i^j=\{\begin{array}{ll}{v}_i^j,& \text{rand}<C{R}_i\text{ 或 }j=j_{\text{rand}}\\ x_i^j,& \text{否则}\end{array}\text{\hspace{1em}(18)}$$

其中 j rand ∈ { 1 , 2 , 3 , ⋯ , D } j_{\text{rand}} \in \{1, 2, 3, \cdots, D\} jrand​∈{1,2,3,⋯,D} 表示均匀随机索引，$CR$ 是交叉率。

每个个体 $x_i$ 都有一个相关的 $p_i$，使用公式(19)通过代计算。

p i = max ⁡ { 2 / N P , 0.2 ⋅ rand } (19) p_i = \max \{2/NP, 0.2 \cdot \text{rand}\} \tag{19} pi​=max{2/NP,0.2⋅rand}(19)

2.3 L-SAHDE[3]

L-SHADE [15] 通过引入线性种群规模缩减（LPSR）策略来平衡开发和探索。在 L-SHADE 中，种群规模 $NP$ 在进化过程中使用线性函数更新，如公式(20)所示。

$$NP=\text{round}\left[\frac{F{E}_s}{F{E}_{s_{\max }}}(N{P}_{\min }-N{P}_{\text{init}})+N{P}_{\text{init}}\right]\text{\hspace{1em}(20)}$$

其中 $N{P}_{\min }$ 和 $N{P}_{\text{init}}$ 是最小和最大种群规模。$F{E}_{s_{\max }}$ 和 $F{E}_s$ 分别是最大和当前评估次数。每一代结束时，从 $P$ 中丢弃最差的个体以满足更新的 $NP$。

此外，对历史记忆 $M_{CR}$ 的更新进行了一些修改，如公式(21)所示。具体来说，当 $M_{CR}$ 更新时，如果 $M_{CR,k}$ 等于终端值 ⊥ 或 $\max (S_{CR})=0$，则 $M_{CR,k}$ 设置为 ⊥。因此，如果 $M_{CR}$ 被分配 ⊥，$M_{CR}$ 将固定在终端值，这将锁定 $C{R}_i$ 直到搜索结束，如公式(22)所示。

$$M_{CR,k}=\{\begin{array}{ll}\perp ,& M_{CR,k}=\perp \text{ 或 }\max (S_{CR}=0)\\ {\text{mean}}_{WL}(S_{CR}),& \text{否则}\end{array}\text{\hspace{1em}(21)}$$

$$C{R}_i=\{\begin{array}{ll}0,& M_{CR,R_i}=\perp \\ \text{rand}(M_{CR,R_i},0.1),& \text{否则}\end{array}\text{\hspace{1em}(22)}$$

在 L-SHADE 中，贪婪因子 $p$ 设置为常数而不是使用公式(19)生成。外部存档大小设置为 $NP\times A_{\text{rate}}$，$A_{\text{rate}}$ 是外部存档大小的控制参数。注意，外部存档大小在进化过程中根据 $NP$ 更新。

2.4. iL-SHADE[4]

iL-SHADE [16] 是 L-SHADE 的扩展版本。与 L-SHADE 不同的主要特征如下。

首先，当前代的 $M_{CR}$ 和 $M_F$ 被考虑用于更新历史记忆，如公式(23)和公式(24)所示。所有 $M_{CR}$ 的条目在开始时设置为 0.8（在 L-SHADE 中设置为 0.5），历史记忆的一个条目保持固定值，即 $M_{CR,H}$ 和 $M_{F,H}$ 在进化过程中始终设置为 0.9。

$$M_{F,k}=\{\begin{array}{ll}{M}_{F,k},& S_F=\varnothing \\ \frac{{\text{mean}}_{WL}(S_F)+M_{F,k}}{2},& \text{else}\end{array}\text{\hspace{1em}(23)}$$
$$M_{CR,k}=\{\begin{array}{ll}\perp ,& M_{CR,k}=\perp \text{ or}\max (S_{CR}=0)\\ \frac{{\text{mean}}_{WL}(S_{CR})+M_{CR,k}}{2},& \text{else}\end{array}\text{\hspace{1em}(24)}$$

其次，$C{R}_i$ 的非常低的值和 $F_i$ 的非常高的值在进化的早期阶段受到限制[16]。具体来说，使用公式(22)和公式(13)生成的 $C{R}_i$ 和 $F_i$ 将被调整如下。

$$C{R}_i=\{\begin{array}{ll}\max (C{R}_i,0.5),& FES<0.25\cdot FE{S}_{\max }\\ \max (C{R}_i,0.25),& 0.25\cdot FE{S}_{\max }\le FES<0.5\cdot FE{S}_{\max }\\ C{R}_i,& 0.5\cdot FE{S}_{\max }\le FES\end{array}\text{\hspace{1em}(25)}$$
$$F_i=\{\begin{array}{ll}\min (F_i,0.7),& FES<0.6\cdot FE{S}_{\max }\\ \min (F_i,0.8),& 0.25\cdot FE{S}_{\max }\le FES<0.5\cdot FE{S}_{\max }\\ \min (F_i,0.9),& 0.5\cdot FE{S}_{\max }\le FES<0.75\cdot FE{S}_{\max }\end{array}\text{\hspace{1em}(26)}$$

最后，使用公式(27)生成一代中所有个体的贪婪因子 $p$。

$$p=P_{\min }+(P_{\max }-P_{\min })\cdot \frac{FES}{FE{S}_{\max }}\text{\hspace{1em}(27)}$$

在 iL-SHADE 中，$P_{\max }$=0.2 和 $P_{\min }$=0.1 在进化过程中。

2.5. jSO[5]

jSO [17] 是 iL-SHADE 的改进变体，采用新的加权版本的变异策略“DE/current-to-pbest-w/1”，如公式(28)所示。

$$v_i=x_i+F{w}_i\cdot (x_{\text{pbest}}-x_i)+F_i\cdot (x_{r_1}-x_{r_2})\text{\hspace{1em}(28)}$$

$$F{w}_i=\{\begin{array}{ll}0.7\cdot F_i,& FES<0.2\cdot FE{S}_{\max }\\ 0.8\cdot F_i,& 0.2\cdot FE{S}_{\max }\le FES<0.4\cdot FE{S}_{\max }\\ 1.2\cdot F_i,& FES\ge 0.4\cdot FE{S}_{\max }\end{array}\text{\hspace{1em}(29)}$$

在新的变异策略中，进化过程的早期阶段采用较小的因子 $F{w}_i$，而在后期阶段，采用较高的因子 $F{w}_i$ 以调整探索和开发[20]。

此外，在进化过程中，$p_{\max }$=0.25 和 $p_{\min }$=$p_{\max }/2$，$M_F$ 值在 jSO 中初始化为 0.3。

2.6. LSHADE-RSP[6]

LSHADE-RSP 是 jSO 的最近增强版本，通过引入 RSP 和调整 $F_i$ 和 $C{R}_i$ 来实现。RSP 基于的变异策略，DE/current-to-pbest-w/r，如公式(30)所示。

$$v_i=x_i+F{w}_i\cdot (x_{\text{pbest}}-x_i)+F_i\cdot (x_{pr1}-x_{pr2})\text{\hspace{1em}(30)}$$

其中 $x_{pr1}$ 表示基于排名概率从种群 $P$ 中选择的向量，$x_{pr2}$ 是基于排名概率从 $P$ 中选择的向量或从 $A$ 中随机选择的向量。个体 $i$ 的选择概率使用公式(31)计算。

$$P{r}_i=\frac{Ran{k}_i}{(Ran{k}_1+Ran{k}_2+\cdots +Ran{k}_{NP})}\text{\hspace{1em}(31)}$$
$$Ran{k}_i=k(NP-i)+1\text{\hspace{1em}(32)}$$

其中最大和最小的排名分别分配给最佳和最差的个体。 i ∈ { 1 , 2 , 3 , ⋯ , N P } i \in \{1, 2, 3, \cdots, NP\} i∈{1,2,3,⋯,NP} 表示种群中排序适应度数组的索引。$k$ 是调整排名选择贪婪度的控制因子[20]。

此外，使用公式(13)和公式(22)在进化过程中生成的 $F_i$ 和 $C{R}_i$ 调整如下。

$$F_i=\{\begin{array}{ll}\min (F_i,0.7),& FES<0.6\cdot FE{S}_{\max }\\ F_i,& 0.6\cdot FE{S}_{\max }\le FES\end{array}\text{\hspace{1em}(33)}$$
$$C{R}_i=\{\begin{array}{ll}\max (C{R}_i,0.6),& FES<0.25\cdot FE{S}_{\max }\\ \max (C{R}_i,0.5),& 0.25\cdot FE{S}_{\max }\le FES<0.5\cdot FE{S}_{\max }\\ C{R}_i,& 0.5\cdot FE{S}_{\max }\le FES\end{array}\text{\hspace{1em}(34)}$$

最后，LSHADE-RSP 中与 jSO 不同的参数设置如下：公式(27)中的 $p_{\max }$ 设置为 0.17，公式(32)中的 $k$ 设置为 3，所有 $M_F$ 的条目初始化为 0.3。

3. 提出的APSM-jSO算法[7]

在过去二十年中，针对差分进化（DE）及其变体在自适应控制参数设置和变异策略修改方面进行了一系列研究。DE最具竞争力的变体是jSO，由Brest于2017年提出，它结合了近年来提出的DE有效改进，并成为IEEE CEC 2017竞赛的获胜者。然而，jSO中的自适应机制可能没有完全发挥其优化潜力。在本文中，开发了一种基于jSO的APSM-jSO，通过对其缩放因子选择、交叉率选择和外部存档更新机制进行简单有效的修改，以充分利用其优化性能。提出的APSM-jSO的详细信息如下。

3.1. 自适应参数选择机制（APSM）

在jSO框架中，缩放因子 $F$ 和交叉率 $CR$ 对其性能[17]起着重要作用。此外，成功的$M_{CR}$ 和 $M_F$ 历史记忆显著提高了jSO的有效性。然而，由于 $M_{CR}$ 和 $M_F$ 中的条目是随机选择用于现有SHADE变体中的，因此历史记忆中的更好条目没有被更频繁地使用以加速进化过程。为了充分利用历史记忆中的更好条目，提出了一种新的自适应参数选择机制，用于从 $M_F$ 和 $M_{CR}$ 中选择条目以生成合适的 $F_i$ 和 $C{R}_i$。在此机制中，根据上一代的历史使用信息为 $M_{CR}$ 和 $M_F$ 中的条目分配不同的概率。具体来说，$M_{CR}$（$M_F$）中条目 $h$ 的选择概率在每一代计算，如公式(35)所示。

$$P{R}_h=\frac{S{R}_h}{{\sum }_{h=1}^{H}S{R}_h},h=1,2,\cdots ,H\text{\hspace{1em}(35)}$$

$$S{R}_h=\frac{S{N}_h}{N_h},h=1,2,\cdots ,H\text{\hspace{1em}(36)}$$

其中 $N_h$ 表示在 $M_{CR}$（$M_F$）中条目 $h$ 生成 $F_i$ 和 $C{R}_i$ 的调用次数，$S{N}_h$ 表示条目 $h$ 生成的 $F_i$ 和 $C{R}_i$ 指示 $u_i$ 生成的个体优于 $x_i$ 的次数。此外，如果 $M_{CR}$ 和 $M_F$ 中的新更新条目等于 $\max (SR)$，则成功次数 $S{R}_h$ 设置为等于 $\max (SR)$。此外，如果试验个体比相应目标个体差，则 $M_{CR}$ 和 $M_F$ 中条目的所有概率将重置为 $1/H$。需要注意的是，仅在进化过程中更新 $M_F$ 和 $M_{CR}$ 中从 1 到 $H-1$ 的条目。

3.2. 先进先出方法（FIFO）

在jSO框架中，如果外部存档大小 $|A|$=$NP\times A_{\text{rate}}$ 达到预定大小，则随机丢弃一个个体以为新插入的个体腾出空间。由于随机更新机制，外部存档中的一些个体可能在许多代中不会被丢弃，这导致外部存档中的一些元素在优化后期被过度使用。为了避免过度使用 $A$ 并丰富种群多样性，引入了先进先出（FIFO）方法，如果存档大小 $|A|$ 达到预定大小，则最早保存的个体将被新插入的个体替换。

3.3. 基于RSP的新变异策略

为了增强APSM-jSO的利用，使用LSHADE-RSP中描述的RSP策略提出了一种新的基于RSP的变异策略，如公式(31)~(32)所示。与LSHADE-RSP不同，RSP仅用于APSM-jSO中的 $r_1$ 而不是 $r_1$ 和 $r_2$，如公式(30)所述。从 $A$ 和 $P$ 的组合中随机选择 $x_{r2}$ 的优势在于，外部存档机制可以在进化的后期充分发挥作用，这可以有效提高种群多样性。此外，基于排名的选择压力策略使 $x_{pr1}$ 具有优于 $x_{r2}$ 的更高概率，即种群的进化方向具有向更好方向进化的更高概率，如图1(a)所示。如图1(b)所示。

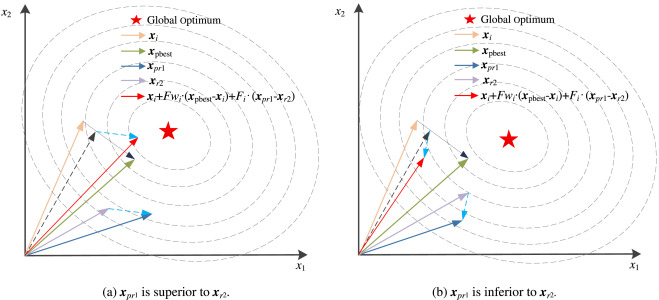
因此，新的基于RSP的变异策略如公式(37)所述。

$$v_i=x_i+F{w}_i\cdot (x_{\text{pbest}}-x_i)+F_i\cdot (x_{pr1}-x_{r2})\text{\hspace{1em}(37)}$$

其中 $x_{r2}$ 是从与 $x_i$、$x_{\text{pbest}}$ 或 $x_{pr1}$ 不同的 $A$ 和 $P$ 的组合中随机选择的个体。

参考文献

[1]DE: Storn, R., Price, K. Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. Journal of Global Optimization 11, 341–359 (1997). https://doi.org/10.1023/A:1008202821328
[2] SHADE：R. Tanabe and A. Fukunaga, “Evaluating the performance of SHADE on CEC 2013 benchmark problems,” 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 2013, pp. 1952-1959, doi: 10.1109/CEC.2013.6557798
[3] L-SHADE：R. Tanabe and A. S. Fukunaga, “Improving the search performance of SHADE using linear population size reduction,” 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 2014, pp. 1658-1665, doi: 10.1109/CEC.2014.6900380
[4] iL-SHADE：J. Brest, M. S. Maučec and B. Bošković, “iL-SHADE: Improved L-SHADE algorithm for single objective real-parameter optimization,” 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 2016, pp. 1188-1195, doi: 10.1109/CEC.2016.7743922
[5] jSO：J. Brest, M. S. Maučec and B. Bošković, “Single objective real-parameter optimization: Algorithm jSO,” 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 2017, pp. 1311-1318, doi: 10.1109/CEC.2017.7969456
[6] LSHADE-RSP：V. Stanovov, S. Akhmedova and E. Semenkin, “LSHADE Algorithm with Rank-Based Selective Pressure Strategy for Solving CEC 2017 Benchmark Problems,” 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 2018, pp. 1-8, doi:
10.1109/CEC.2018.8477977
[7] APSM-jSO：Yintong Li, Tong Han, Huan Zhou, Yujie Wei, Yuan Wang, Mulai Tan, Changqiang Huang. % APSM-jSO: A novel jSO variant with an adaptive parameter selection mechanism and a new external archive updating mechanism. % Swarm and Evolutionary Computation, https://doi.org/10.1016/j.swevo.2023.101283