递归实现
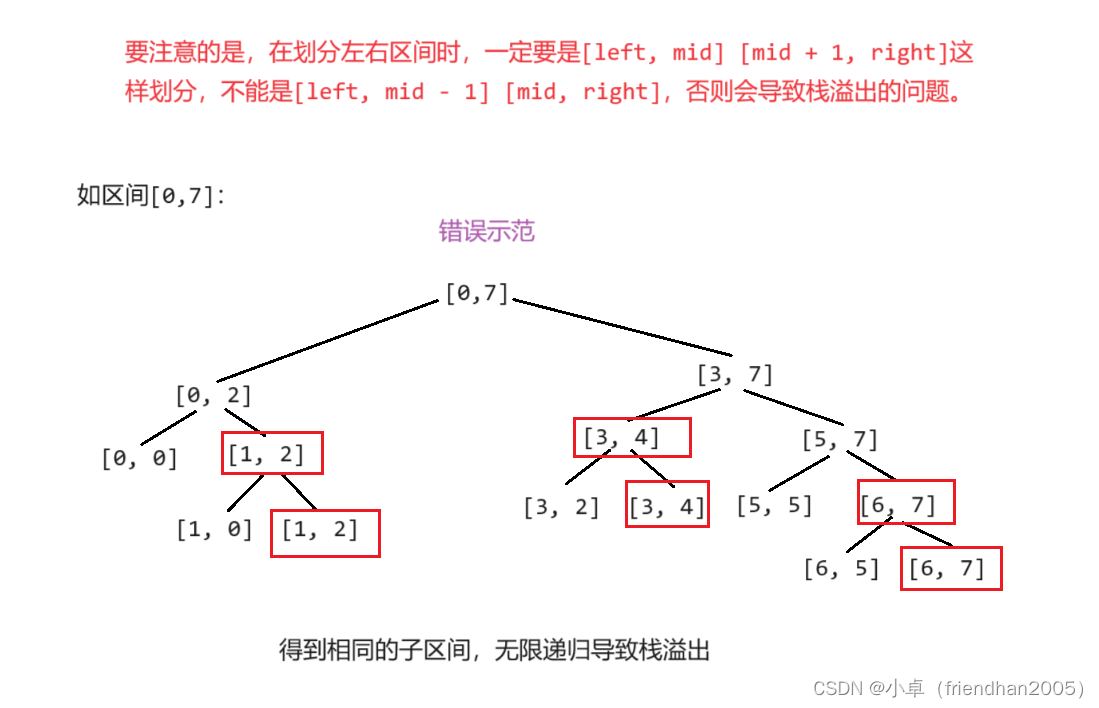
归并排序有点类似于二叉树的后序遍历,是一种基于分治思想的排序算法。具体过程如下:

但要注意,在归并时要额外开辟一个与原数组同等大小的空间用来存储每次归并排序后的值,然后再拷贝到原数组中。
代码实现:
#include<stdlib.h>
#include<string.h>// 归并排序递归实现
void _MergeSort(int* a, int* tmp, int left, int right)
{//当区间只有一个值或没有值时,返回if (left >= right){return;}int mid = (left + right) / 2;//递归左右区间_MergeSort(a, tmp, left, mid);_MergeSort(a, tmp, mid + 1, right);//归并int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int i = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}//将数据拷贝到原数组中memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));
}void MergeSort(int* a, int n)
{//开辟与a同等大小的空间int* tmp = (int*)malloc(sizeof(int) * n);//实现归并的函数_MergeSort(a, tmp, 0, n - 1);free(tmp);tmp = NULL;
}
非递归实现
在实现快排时,我们用栈来实现非递归,但归并排序时,我们用栈来实现似乎有些麻烦。快排在递归到底时,就已经数组排为有序,但层序遍历不行,层序遍历在递归至最底层时才开始排序,如果要用栈来实现,就需要用两个栈来存储,且过程很麻烦。
因此,在这里我们采用循环的方式来实现层序遍历的非递归。先来看具体过程:
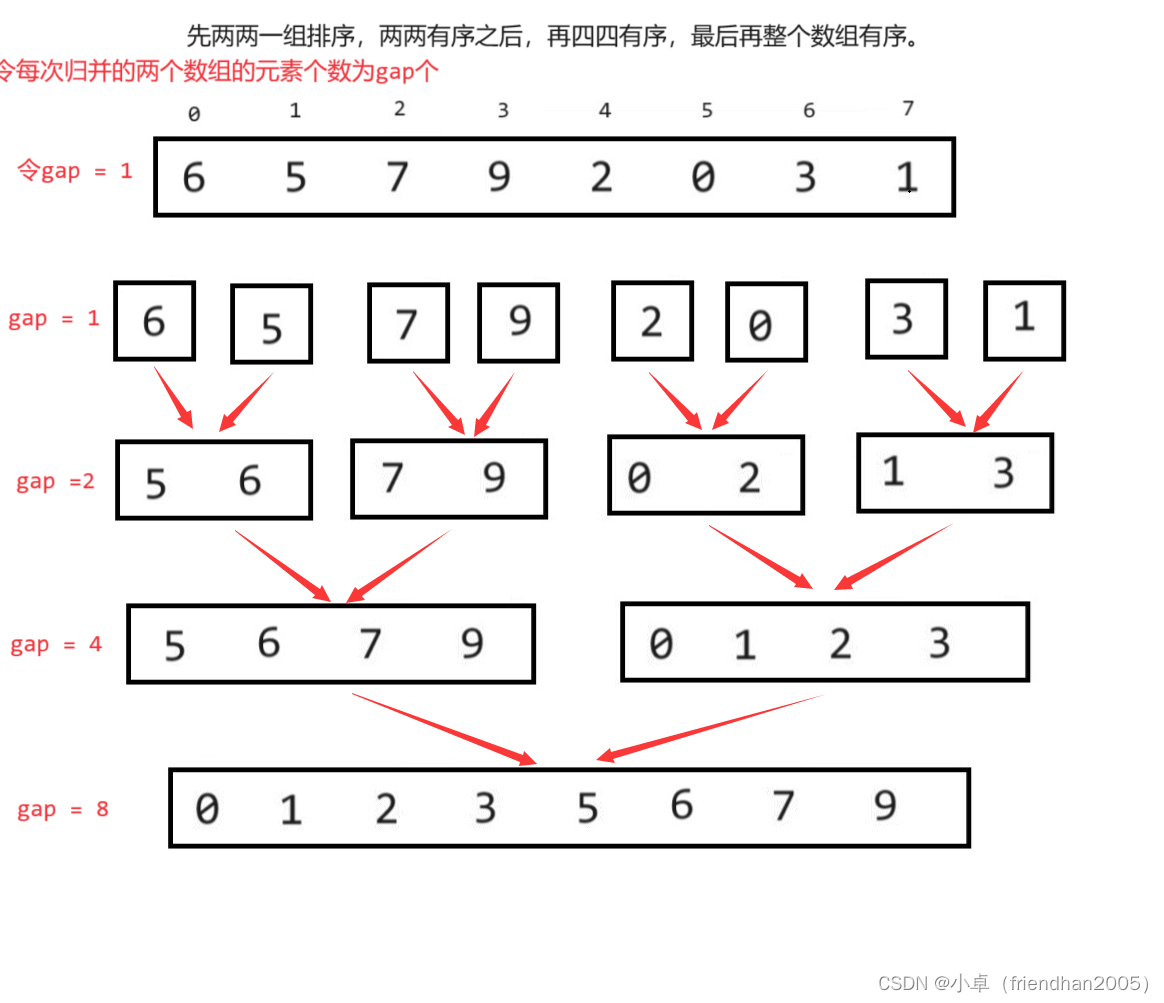
根据上图我们可以得到代码:(但这个代码只能实现2的次方倍的数组个数的排序,其它的会出现数组越界的问题)
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{//开辟与a同等大小的空间int* tmp = (int*)malloc(sizeof(int) * n);//归并int gap = 1;//gap为归并的每组数据的个数while (gap < n){//i控制每次归并的起始位置的下标for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}//将数据拷贝到原数组中memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}gap = 2 * gap;}free(tmp);tmp = NULL;
}要想实现数组归并排序的非递归,我们还要再继续解决数组越界的问题。
先来看越界情况的分析:
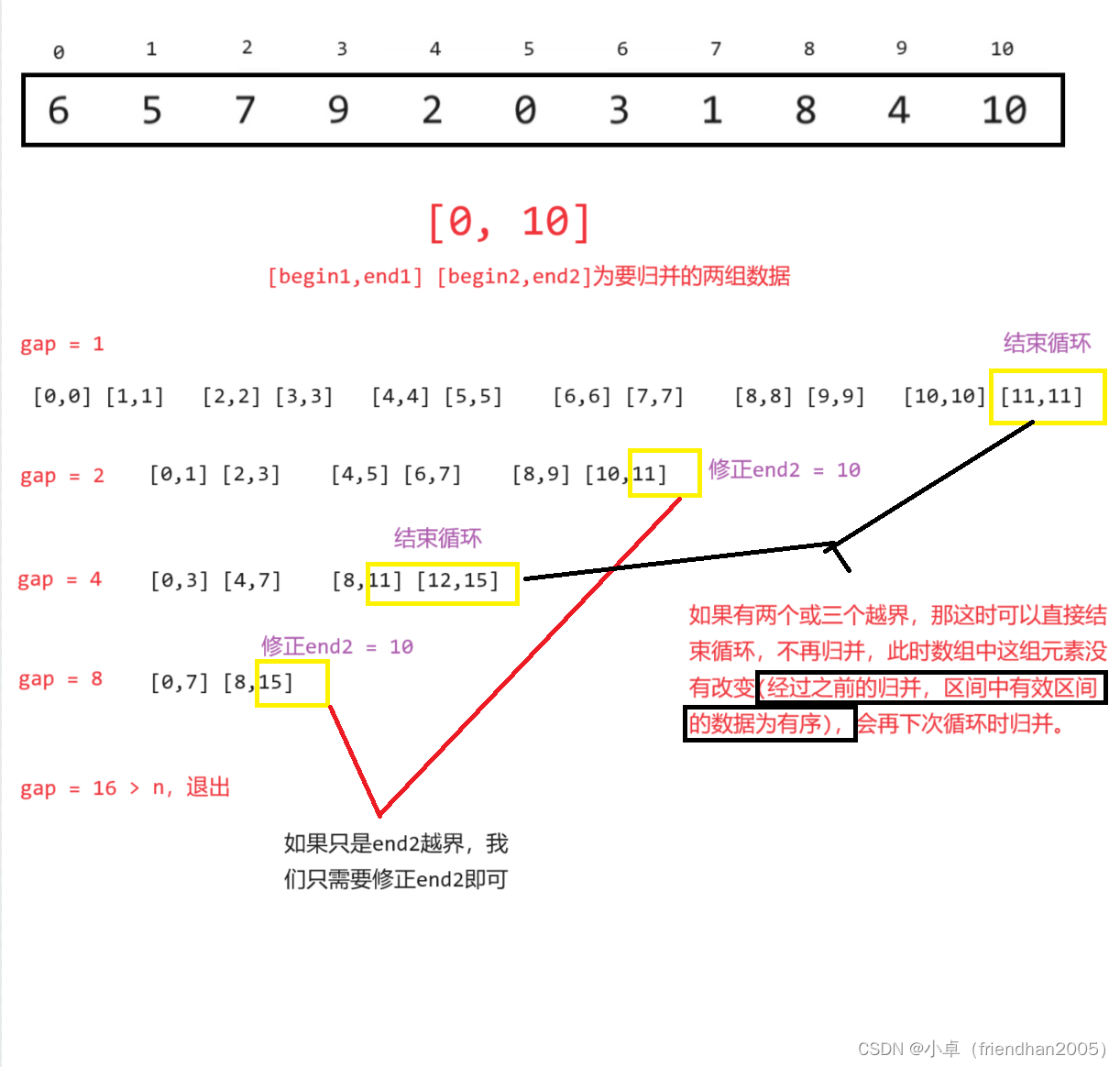
代码实现:
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{//开辟与a同等大小的空间int* tmp = (int*)malloc(sizeof(int) * n);//归并int gap = 1;//gap为归并的每组数据的个数while (gap < n){//i控制每次归并的起始位置的下标for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int j = i;//结束循环if (begin2 >= n){break;}//修正end2if (end2 >= n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}//将数据拷贝到原数组中memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}gap = 2 * gap;}free(tmp);tmp = NULL;
}完整代码
#include<stdio.h>
#include<stdlib.h>
#include<string.h>void Print(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}// 归并排序递归实现
void _MergeSort(int* a, int* tmp, int left, int right)
{//当区间只有一个值或没有值时,返回if (left >= right){return;}int mid = (left + right) / 2;//递归左右区间_MergeSort(a, tmp, left, mid);_MergeSort(a, tmp, mid + 1, right);//归并int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int i = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}//将数据拷贝到原数组中memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));
}void MergeSort(int* a, int n)
{//开辟与a同等大小的空间int* tmp = (int*)malloc(sizeof(int) * n);//实现归并的函数_MergeSort(a, tmp, 0, n - 1);free(tmp);tmp = NULL;
}// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{//开辟与a同等大小的空间int* tmp = (int*)malloc(sizeof(int) * n);//归并int gap = 1;//gap为归并的每组数据的个数while (gap < n){//i控制每次归并的起始位置的下标for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int j = i;//结束循环if (begin2 >= n){break;}//修正end2if (end2 >= n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}//将数据拷贝到原数组中memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}gap = 2 * gap;}free(tmp);tmp = NULL;
}int main()
{int arr[] = { 6,5,7,9,2,0,3,1,8,4,10 };int len = sizeof(arr) / sizeof(int);MergeSortNonR(arr, len);Print(arr, len);return 0;
}













