题目描述
给你 n 根火柴棍,你可以拼出多少个形如 A+B=C 的等式?等式中的 A、B、C 是用火柴棍拼出的整数(若该数非零,则最高位不能是 0)。用火柴棍拼数字 0∼9 的拼法如图所示:
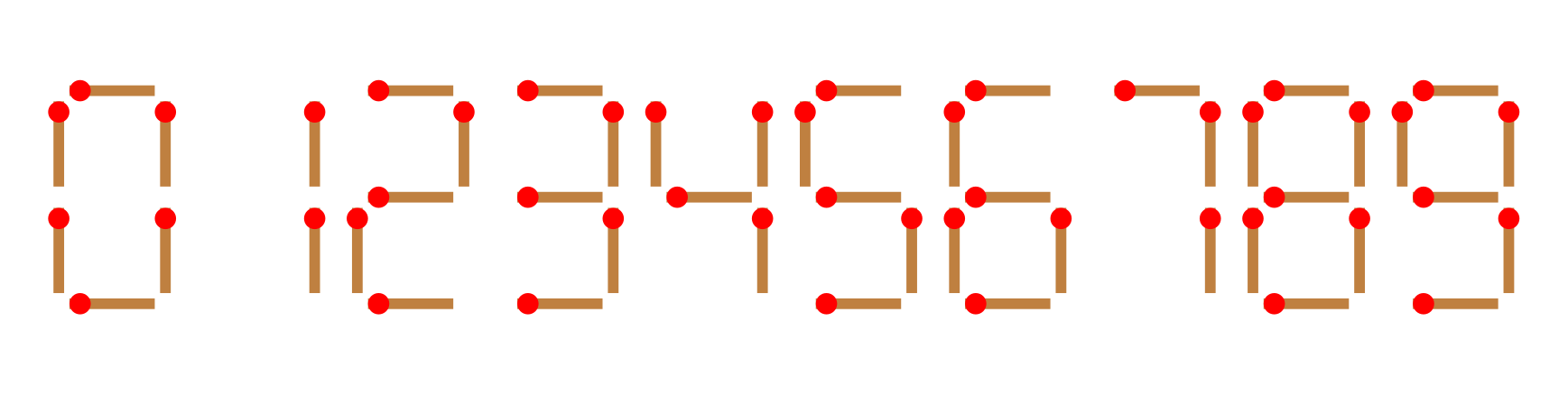
注意:
- 加号与等号各自需要两根火柴棍;
- 如果 A=B,则 A+B=C 与 B+A=C 视为不同的等式(A,B,C≥0);
- n 根火柴棍必须全部用上。
输入格式
一个整数 n(1≤n≤24)。
输出格式
一个整数,能拼成的不同等式的数目。
输入输出样例
输入 #1复制
14
输出 #1复制
2
输入 #2复制
18
输出 #2复制
9
说明/提示
【输入输出样例 1 解释】
2 个等式为 0+1=1 和 1+0=1。
【输入输出样例 2 解释】
9 个等式为
0+4=4、0+11=11、1+10=11、2+2=4、2+7=9、4+0=4、7+2=9、10+1=11、11+0=11。
题目链接:P1149 [NOIP 2008 提高组] 火柴棒等式 - 洛谷
学习链接:DFS正确入门方式 | DFS + 递归与递推习题课(上) | 一节课教你爆搜!_哔哩哔哩_bilibili
解题思路:
- 枚举三层的全排列 _ _ _,数字范围为0~711,即711+0=711,刚好等于n根火柴棍
- 设置一个桶t[],将每个未选过的数字装进去试探是否符合条件
- 若A+B=C,且这个等式的火柴棍之和fire_num = n ,则累计排列方案
- 剪枝:枚举到火柴棍数量超过n,结束搜索
代码如下:
#include<bits/stdc++.h>
using namespace std;
int n;//火柴棍数量
int t[1000];//记录排列方案
int a[1000]={6,2,5,5,4,5,6,3,7,6};//记录每个整数所含的火柴棍
int cnt=0;//累计符合条件的方案数 //计算整数所含的火柴棍数
int caculate(int num)
{//若该整数已经在火柴棍数组中存在,直接返回其数量 if(a[num]>0) return a[num];else{int sum=0;int x=num;while(x>0){sum=sum+a[x%10];x=x/10;}return a[num]=sum;}}
void dfs(int x,int fire_num)
{//剪枝:若此时枚举的火柴棍数量已经超过了n,结束搜索if(fire_num>n) return ; //如果枚举超过3个位置,结束搜索if(x>3){//判断火柴棍数量是否==n && 且满足 A+B=C if(fire_num==n && t[1]+t[2]==t[3]){cnt++;//累计方案数 } return ;//结束搜素 } for(int i=0;i<=1000;i++){//将整数装入桶t[]t[x]=i;//开始枚举下一个位置,并累计火柴棍数量dfs(x+1,fire_num+caculate(i));//将整数撤出桶,便于下一个整数的放入,搜索下一个排列 t[x]=0; }
}
int main()
{//除去 + 和 = 各自两根火柴棍cin>>n;n=n-4;// //对于10~1000的整数所含的火柴棍数量也可以用递推计算出
// for(int i=10;i<=1000;i++)
// {
// a[i]=a[i%10]+a[i/10];
// } dfs(1,0);//从第一个位置开始枚举 //输出方案数cout<<cnt<<endl; return 0;
}希望能帮助到各位同志,祝天天开心,学业进步!














