笔记100：使用 OSQP-Eigen 对 MPC 进行求解的方法与代码

1. 前言：

我们在对系统进行建模的时候，为了减少计算量，一般都将系统简化为线性的，系统如果有约束，也是将约束简化为线性的；

因此本篇博客只针对两种常见系统模型的 MPC 问题进行求解：

线性系统 + 无约束
线性系统 + 线性约束

2. 线性系统 + 无约束的 MPC 问题求解

目前已知：

目标（代价）函数：
- $J=\sum_{k=0}^{N-1}[x_{k}^TQx_{k}+u_{k}^TRu_{k}]+x_{N}^TPx_{N}$
- 矩阵 $Q$ ， $R$ ， $P$ 均为正定矩阵；
线性系统状态空间方程： $x(k+1)=Ax(k)+Bu(k)$
当前时间步 k = 0 时系统的初始状态量： $x(0)$

注：代价函数和状态空间方程中的状态量 x 已经是误差量了；

求解方法：

动态规划（针对无约束的问题，根本不需要使用到二次规划，直接使用动态规划即可求解）

进行求解：

3. 线性系统 + 线性约束的 MPC 问题求解

目前已知：

目标（代价）函数：
- $J=\sum_{k=0}^{N-1}[(x_{k}-x_{r})^TQ(x_{k}-x_{r})+u_{k}^TRu_{k}]+(x_{N}-x_{r})^TQ_{N}(x_{N}-x_{r})$
- 矩阵 $Q$ ， $R$ ， $Q_{N}$ 均为正定矩阵；
线性系统状态空间方程： $x(k+1)=Ax(k)+Bu(k)$
当前时间步 k = 0 时的初始状态量： $x_{0}$
系统的目标状态值： $x_{r}$
线性约束条件：
- 线性等式约束： $x(k+1)=Ax(k)+Bu(k)$
- 线性不等式约束：
  - $x_{min}\leq x\leq x_{max}$
  - $u_{min}\leq u\leq u_{max}$

注：代价函数和状态空间方程中的 x 并不是误差量， $x_{k}-x_{r}$ 才是误差量；

求解方法：

二次规划
解释：因为系统带了约束，所以动态规划方法已经不好使了，这种方法无法处理带有约束条件的问题，而二次规划方法可以用来处理带有约束条件的问题，所以需要我们将问题等价转换为二次规划的形式，再调用 OSQP 求解；

3.1 将问题转化为二次规划的形式

（1）目标：

（2）代价函数的转化过程：

（3）约束条件转化：

参考文章：LQR、MPC以及osqp库_osqp mpc-CSDN博客

3.2 使用 OSQP-Egine 库求解二次规划问题

原始问题：

QP 问题：

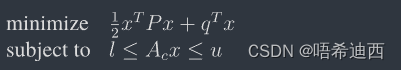
QP 问题中涉及的矩阵和向量：

代码：

#include "OsqpEigen/OsqpEigen.h"    // osqp-eigen
#include <Eigen/Dense>              // eigen
#include <iostream>// 函数作用：对矩阵 A / B 赋值
// 注意：这个函数根据自己实际的需要进行赋值
void setDynamicsMatrices(Eigen::Matrix<double, 12, 12>& a, Eigen::Matrix<double, 12, 4>& b) {a << 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0.,0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0.0488, 0., 0., 1., 0., 0., 0.0016,0., 0., 0.0992, 0., 0., 0., -0.0488, 0., 0., 1., 0., 0., -0.0016, 0., 0., 0.0992, 0., 0.,0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.0992, 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0.,0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0.,0., 0., 0.9734, 0., 0., 0., 0., 0., 0.0488, 0., 0., 0.9846, 0., 0., 0., -0.9734, 0., 0., 0.,0., 0., -0.0488, 0., 0., 0.9846, 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.9846;b << 0., -0.0726, 0., 0.0726, -0.0726, 0., 0.0726, 0., -0.0152, 0.0152, -0.0152, 0.0152, -0.,-0.0006, -0., 0.0006, 0.0006, 0., -0.0006, 0.0000, 0.0106, 0.0106, 0.0106, 0.0106, 0,-1.4512, 0., 1.4512, -1.4512, 0., 1.4512, 0., -0.3049, 0.3049, -0.3049, 0.3049, -0.,-0.0236, 0., 0.0236, 0.0236, 0., -0.0236, 0., 0.2107, 0.2107, 0.2107, 0.2107;
}// 函数作用：对向量 x_min / x_max / u_min / u_max 赋值
// 注意：这个函数根据自己实际的需要进行赋值
void setInequalityConstraints(Eigen::Matrix<double, 12, 1>& xMax,Eigen::Matrix<double, 12, 1>& xMin,Eigen::Matrix<double, 4, 1>& uMax,Eigen::Matrix<double, 4, 1>& uMin) {// 注意：因为 MPC 输出的当前时刻控制量是基于上一时刻控制量的增量// 解释：当前时刻为 0，上一时刻为 -1，所以这个 u0 代表的是 -1 时刻的控制量大小double u0 = 10.5916;uMin << 9.6 - u0, 9.6 - u0, 9.6 - u0, 9.6 - u0;uMax << 13 - u0, 13 - u0, 13 - u0, 13 - u0;xMin << -M_PI / 6, -M_PI / 6, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -1., -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY;xMax << M_PI / 6, M_PI / 6, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY, OsqpEigen::INFTY;
}// 函数作用：对矩阵 Q / R 赋值
// 注意：这个函数根据自己实际的需要进行赋值
void setWeightMatrices(Eigen::DiagonalMatrix<double, 12>& Q, Eigen::DiagonalMatrix<double, 4>& R) {Q.diagonal() << 0, 0, 10., 10., 10., 10., 0, 0, 0, 5., 5., 5.;R.diagonal() << 0.1, 0.1, 0.1, 0.1;
}// 函数作用：对稀疏矩阵 P 赋值
void castMPCToQPHessian(const Eigen::DiagonalMatrix<double, 12>& Q,const Eigen::DiagonalMatrix<double, 4>& R,int mpcWindow,Eigen::SparseMatrix<double>& hessianMatrix) {hessianMatrix.resize(12 * (mpcWindow + 1) + 4 * mpcWindow, 12 * (mpcWindow + 1) + 4 * mpcWindow);// 使用 Q / R 填充稀疏矩阵 Pfor (int i = 0; i < 12 * (mpcWindow + 1) + 4 * mpcWindow; i++) {if (i < 12 * (mpcWindow + 1)) {int posQ = i % 12;float value = Q.diagonal()[posQ];if (value != 0) hessianMatrix.insert(i, i) = value;}else {int posR = i % 4;float value = R.diagonal()[posR];if (value != 0) hessianMatrix.insert(i, i) = value;}}
}// 函数作用：赋值向量 q
void castMPCToQPGradient(const Eigen::DiagonalMatrix<double, 12>& Q,const Eigen::Matrix<double, 12, 1>& xRef,int mpcWindow,Eigen::VectorXd& gradient) {Eigen::Matrix<double, 12, 1> Qx_ref;Qx_ref = Q * (-xRef);// 填充向量 qgradient = Eigen::VectorXd::Zero(12 * (mpcWindow + 1) + 4 * mpcWindow, 1);for (int i = 0; i < 12 * (mpcWindow + 1); i++) {int posQ = i % 12;float value = Qx_ref(posQ, 0);gradient(i, 0) = value;}
}// 函数作用：赋值稀疏矩阵 A_c
void castMPCToQPConstraintMatrix(const Eigen::Matrix<double, 12, 12>& dynamicMatrix,    // Aconst Eigen::Matrix<double, 12, 4>& controlMatrix,     // Bint mpcWindow,Eigen::SparseMatrix<double>& constraintMatrix) {constraintMatrix.resize(12 * (mpcWindow + 1) + 12 * (mpcWindow + 1) + 4 * mpcWindow, 12 * (mpcWindow + 1) + 4 * mpcWindow);// 等式约束 -- 填充for (int i = 0; i < 12 * (mpcWindow + 1); i++) {constraintMatrix.insert(i, i) = -1;}// 填充 A_c 矩阵中的 Afor (int i = 0; i < mpcWindow; i++) {for (int j = 0; j < 12; j++) {for (int k = 0; k < 12; k++) {float value = dynamicMatrix(j, k);if (value != 0) constraintMatrix.insert(12 * (i + 1) + j, 12 * i + k) = value;}}}// 填充 A_c 矩阵中的 Bfor (int i = 0; i < mpcWindow; i++) {for (int j = 0; j < 12; j++) {for (int k = 0; k < 4; k++) {float value = controlMatrix(j, k);if (value != 0) {constraintMatrix.insert(12 * (i + 1) + j, 4 * i + k + 12 * (mpcWindow + 1)) = value;}}}}// 不等式约束 -- 填充for (int i = 0; i < 12 * (mpcWindow + 1) + 4 * mpcWindow; i++) {constraintMatrix.insert(i + (mpcWindow + 1) * 12, i) = 1;}
}// 函数作用：赋值左右约束 l / u
void castMPCToQPConstraintVectors(const Eigen::Matrix<double, 12, 1>& xMax,const Eigen::Matrix<double, 12, 1>& xMin,const Eigen::Matrix<double, 4, 1>& uMax,const Eigen::Matrix<double, 4, 1>& uMin,const Eigen::Matrix<double, 12, 1>& x0,int mpcWindow,Eigen::VectorXd& lowerBound,Eigen::VectorXd& upperBound) {// 不等式约束的左右边界数组：[xmin , xmin , ... , xmin | umin , umin , ... umin ]Eigen::VectorXd lowerInequality = Eigen::MatrixXd::Zero(12 * (mpcWindow + 1) + 4 * mpcWindow, 1);Eigen::VectorXd upperInequality = Eigen::MatrixXd::Zero(12 * (mpcWindow + 1) + 4 * mpcWindow, 1);for (int i = 0; i <= mpcWindow; i++) {lowerInequality.block(12 * i, 0, 12, 1) = xMin;upperInequality.block(12 * i, 0, 12, 1) = xMax;}for (int i = 0; i < mpcWindow; i++) {lowerInequality.block(4 * i + 12 * (mpcWindow + 1), 0, 4, 1) = uMin;upperInequality.block(4 * i + 12 * (mpcWindow + 1), 0, 4, 1) = uMax;}// 不全数组 l / u 的上半部分：[ -x0 , 0 , 0 , ... , 0 ]Eigen::VectorXd lowerEquality = Eigen::MatrixXd::Zero(12 * (mpcWindow + 1), 1);Eigen::VectorXd upperEquality;lowerEquality.block(0, 0, 12, 1) = -x0;upperEquality = lowerEquality;lowerEquality = lowerEquality;// 将数组融合，得到真正的上下边界数组 l / ulowerBound = Eigen::MatrixXd::Zero(2 * 12 * (mpcWindow + 1) + 4 * mpcWindow, 1);    // 分配内存空间lowerBound << lowerEquality, lowerInequality;upperBound = Eigen::MatrixXd::Zero(2 * 12 * (mpcWindow + 1) + 4 * mpcWindow, 1);    // 分配内存空间upperBound << upperEquality, upperInequality;
}// 函数作用：更新约束边界 l 和 u
void updateConstraintVectors(const Eigen::Matrix<double, 12, 1>& x0,Eigen::VectorXd& lowerBound,Eigen::VectorXd& upperBound) {lowerBound.block(0, 0, 12, 1) = -x0;upperBound.block(0, 0, 12, 1) = -x0;
}double getErrorNorm(const Eigen::Matrix<double, 12, 1>& x, const Eigen::Matrix<double, 12, 1>& xRef) {Eigen::Matrix<double, 12, 1> error = x - xRef;  // 计算误差（对比目标状态 xref 和当前状态 x0 之间的差距）return error.norm();                            // 返回误差的二范数
}// 主函数：
int main() {// 设定有限时域长度：int mpcWindow = 20;// 初始化原始问题涉及到的矩阵：Eigen::DiagonalMatrix<double, 12> Q;        // Q    （对角阵）Eigen::DiagonalMatrix<double, 4> R;         // R    （对角阵）Eigen::Matrix<double, 12, 12> a;            // A    （状态量 x 的维数为 12）Eigen::Matrix<double, 12, 4> b;             // B    （控制量 u 的维数为 4 ）Eigen::Matrix<double, 12, 1> xMax;          // x_maxEigen::Matrix<double, 12, 1> xMin;          // x_minEigen::Matrix<double, 4, 1> uMax;           // u_maxEigen::Matrix<double, 4, 1> uMin;           // u_minEigen::Matrix<double, 12, 1> x0;            // x_0Eigen::Matrix<double, 12, 1> xRef;          // x_ref// 指定初始值和参考值：x0 << 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0;xRef << 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0;// 初始化 QP 问题涉及到的矩阵：// 注意：这里只是初始化了名字，并未指定分配的内存空间的大小Eigen::SparseMatrix<double> hessian;        // P    （稀疏矩阵）Eigen::VectorXd gradient;                   // qEigen::SparseMatrix<double> linearMatrix;   // A_c  （稀疏矩阵）Eigen::VectorXd lowerBound;                 // lEigen::VectorXd upperBound;                 // u// 对原始问题中的矩阵进行赋值：// 注意：这些函数根据自己实际的需要进行赋值，不同的系统这些矩阵的值肯定是不一样的setWeightMatrices(Q, R);                            // 赋值矩阵 Q / RsetDynamicsMatrices(a, b);                          // 赋值矩阵 A / BsetInequalityConstraints(xMax, xMin, uMax, uMin);   // 赋值约束条件// 对 QP 问题中的矩阵进行赋值：// 注意：这些函数不需要调整，固定的函数格式，因为都是通过上面原始问题的矩阵进行赋值的，只要传入的原始矩阵被修改了就行了castMPCToQPHessian(Q, R, mpcWindow, hessian);                                                   // 赋值稀疏矩阵 PcastMPCToQPGradient(Q, xRef, mpcWindow, gradient);                                              // 赋值向量 qcastMPCToQPConstraintMatrix(a, b, mpcWindow, linearMatrix);                                     // 赋值稀疏矩阵 A_ccastMPCToQPConstraintVectors(xMax, xMin, uMax, uMin, x0, mpcWindow, lowerBound, upperBound);    // 赋值左右约束 l / u// 创建求解器：// 注意：这句话只是实例化了一个求解器对象，但并未对其进行任何的配置OsqpEigen::Solver solver;// 配置求解器的设置：solver.settings()->setVerbosity(true);// 解释：这行代码会设置求解器的输出冗长程度，setVerbosity(false) 会关闭求解器的详细输出，使其在求解过程中不输出额外的信息，这在需要安静地运行求解器时非常有用；solver.settings()->setWarmStart(true);// 解释：启用 WarmStart 功能，加快求解速度（启用 WarmStart 意味着求解器在求解问题时，可以利用之前求解的结果作为初始猜测来加速收敛，这在处理连续求解类似问题时特别有用，可以显著减少计算时间）；// 配置求解器的数据：// 包括：变量数目 + 约束数目 + 矩阵P + 梯度向量q + 线性约束矩阵A_c + 变量下界l + 上界u// 解释：如果传入失败，各个函数返回值为 falsesolver.data()->setNumberOfVariables(12 * (mpcWindow + 1) + 4 * mpcWindow);          // 设置优化问题的变量数目（ x_0 ~ x_N  +  u_0 ~ u_N-1 ）solver.data()->setNumberOfConstraints(2 * 12 * (mpcWindow + 1) + 4 * mpcWindow);    // 设置优化问题的约束数目if (!solver.data()->setHessianMatrix(hessian)) return 1;                            // 传入 P 矩阵if (!solver.data()->setGradient(gradient)) return 1;                                // 传入 q 向量if (!solver.data()->setLinearConstraintsMatrix(linearMatrix)) return 1;             // 传入 A_c 矩阵if (!solver.data()->setLowerBound(lowerBound)) return 1;                            // 传入 lif (!solver.data()->setUpperBound(upperBound)) return 1;                            // 传入 u// 初始化求解器：// 解释：使用上面已经传入 settings() 和 data() 的配置参数，来初始化求解器if (!solver.initSolver()) return 1;// 定义矩阵存放：控制输入 / 求解器输出的解Eigen::Vector4d ctr;            // 存储 MPC 控制器输出的控制量Eigen::VectorXd QPSolution;     // 存储求解器的解// 定义求解器最大迭代次数int numberOfSteps = 50;// 开始求解：for (int i = 0; i < numberOfSteps; i++) {// 使用求解器 solver 求解 QP 问题if (solver.solveProblem() != OsqpEigen::ErrorExitFlag::NoError) return 1;// 将 QP 问题的解存储在向量 QPSolution 中QPSolution = solver.getSolution();// 取解的第一个时间步的控制量 u0 放入向量 ctr 中ctr = QPSolution.block(12 * (mpcWindow + 1), 0, 4, 1);// 将当前时间步 0 处的状态 x0 的数据保存到 x0Data 中auto x0Data = x0.data();// 更新当前状态，时间步往前走一步x0 = a * x0 + b * ctr;// 根据更新后的 x0 值更新约束 l 和 u// 解释：x0 的变化只会影响 l 和 u，而不会对矩阵 A_c / P / q 造成影响updateConstraintVectors(x0, lowerBound, upperBound);// 将更新后的约束边界应用于求解器if (!solver.updateBounds(lowerBound, upperBound)) return 1;}return 0;
}