免费网址软件_免费咨询健康_最新最好的磁力搜索_品牌策划方案怎么写

ok, 今天我简单整理了一下用cpp写的一些二叉树拓展的算法题, 有兴趣可以来浏览一波. 对于这些题目呢, 整体难度不大, 不过我听学长学姐说面试官挺喜欢考这部分题目的, 能够很好的考察了一个学生对于二叉树这块内容的一个掌握情况.

- T1: 单值二叉树
- T2: 对称二叉树
- T3: 二叉树的前序遍历(递归写法)
- T4: 镜像二叉树
- T5: 判断一棵树是否是另一棵树的子树
- T6: 相同的树
- T7: 根据二叉树创建字符串
- T8: 二叉树的层序遍历以及层序遍历2
- T9: 二叉树的最近公共祖先
- T10: 将二叉搜索树转换为排序的双向链表
- T11: 从前序与中序遍历中构建二叉树
- T12: 二叉树的前序/中序/后续遍历(非递归形式)
- - 1. 前序遍历
  - 2. 中序遍历
  - 3. 后序遍历

T1: 单值二叉树

题目链接: https://leetcode.cn/problems/univalued-binary-tree/description/
整体思路: 我们就盯着一颗最小的基本单元看, 即假设一棵树只有根, 左子树是一个结点, 右子树也是一个结点, 我们比较他是不是一棵单值二叉树即可, 我们判断这个单值二叉树不要找对的, 而是要找不满条件的, 如果左子树结点与根不一致, 那么我们就返回false; 右子树结点同理.
递归子问题: 根与左节点的val值是否一致? 根与右结点的val值是否一致?

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isUnivalTree(TreeNode* root) {//如果root是空, 那么是满足条件的if(root == nullptr)return true;//如果根的左子树存在, 且左子树val与根的val不一致, 返回falseif(root->left && root->left->val != root->val) return false;//如果根的右子树存在, 且右子树val与根的val不一致, 返回falseif(root->right && root->right->val != root->val)return false;//当前子树找完了, 并不代表整棵树没有问题, 我们继续看看他的左子树 和 右子树是否有问题. return isUnivalTree(root->left) && isUnivalTree(root->right);}
};

T2: 对称二叉树

题目链接: https://leetcode.cn/problems/symmetric-tree/
整体思路: 先看一颗最基本的树, 如果这棵树左右都是空, 满足条件. 如果这棵树一个为空一个不为空, 不满足条件. 如果这棵树左右结点都有但是val不一样, 不满足条件. 如果上述条件都满足, 我们再看看他的子树是否满足~
递归子问题: 左节点与右结点的value值是否一致?

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool _isSymmetric(TreeNode* left, TreeNode* right) {//如果左右同时为空, 则符合条件. if(!left && !right) return true;//如果左右只有一个为空, 则不符合条件, 返回false. if(!left || !right) return false;//此时, 左节点和右结点都有~if(left->val != right->val) return false;return _isSymmetric(left->left, right->right) && _isSymmetric(left->right, right->left); }bool isSymmetric(TreeNode* root) {//我们假设这棵树最简单的形态就是一个根, 左子树一个结点, 右子树一个结点. 此时如何比较? return _isSymmetric(root->left, root->right);}
};

T3: 二叉树的前序遍历(递归写法)

题目链接: https://leetcode.cn/problems/binary-tree-preorder-traversal/
整体思路: 在一颗最简单的二叉树中, 先访问根, 在访问左子树, 在左子树中, 先访问根, 在访问左子树的左子树… 最后在访问右子树的根, 右子树的左子树…
递归子问题: 先访问根, 再访问左子树, 最后访问右子树.

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void _preorderTraversal(vector<int>& v, TreeNode* root){if(root == nullptr) return; //如果是空的话, 我们就直接返回即可~ v.push_back(root->val); //先访问根_preorderTraversal(v, root->left); //在访问左子树_preorderTraversal(v, root->right); //最后是右子树}vector<int> preorderTraversal(TreeNode* root) {vector<int> ret;_preorderTraversal(ret, root); //这个地方咋又弄个子函数呢? 实际上不弄个子函数也可以, 只不过vector就需要去定义到函数外边去了~ 我们把vector作为一个参数去给到子函数去让他push值, 算是一种方法吧, 当然也可以定义成全局变量咯~ return ret;}
};

T4: 镜像二叉树

题目链接: https://leetcode.cn/problems/invert-binary-tree/description/
整体思路: 根结点的指向, 左右子树交换.
递归子问题: 左子树的左右交换右子树的左右交换根的左右交换…

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if(!root) return nullptr; //如果root是空, 就不用再递归了, 直接返回nullptr即可TreeNode* left = invertTree(root->left); //拿到左子树的根TreeNode* right = invertTree(root->right); //拿到右子树的根//swap(left, right); //交换左右子树的根 -> 为啥这么写不对? 肯定不对啊, left和right是两个临时局部变量, 是left和right本来地址的一个临时拷贝, 你交换这个临时拷贝没啥意义. swap(root->left, root->right);return root; //返回根}
};

T5: 判断一棵树是否是另一棵树的子树

题目链接: https://leetcode.cn/problems/subtree-of-another-tree/description/
整体思路: 找匹配的结点, 如果匹配上了, 那么我们就看看两棵树是否是isSameTree, 如果是, 就返回true, 如果不是我们就继续找~
递归子问题: 这棵树可能是子树吗? 这棵树的左子树可能是子树吗? 右子树呢?

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSameTree(TreeNode* root1, TreeNode* root2){if(!root1 && !root2) return true;if(!root1 || !root2) return false;if(root1->val != root2->val) return false;return isSameTree(root1->left, root2->left) && isSameTree(root1->right, root2->right);}bool isSubtree(TreeNode* root, TreeNode* subRoot) {if(root == nullptr) return false; //一条路径找到头了就返回false, 递归回去就会找下一条路径的. if(root->val == subRoot->val) //如果结点一致, 我们判断一下是不是子树{bool node = isSameTree(root, subRoot);if(node) return true; //如果是子树, 我们就返回即可; 如果不是子树, 那就不返回, 继续找~ }return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);}
};

//写法2: 
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {return root == NULL ? false : isSameTree(root, subRoot) || isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

细节: 这个题目有个细节就是判断isSameTree之后, 如果是就返回true, 如果不是这条路径还要继续找, 而不是不找这条路径了~

T6: 相同的树

题目链接: https://leetcode.cn/problems/same-tree/description/
整体思路: 比较两棵树的根, 比较两棵树的左子树, 比较两棵树的右子树
递归子问题: 根是否一致?

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution 
{
public:bool isSameTree(TreeNode* p, TreeNode* q) {if(p == NULL && q == NULL) return true;if(p == NULL || q == NULL) return false;if(p->val != q->val) return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);}
};

T7: 根据二叉树创建字符串

题目链接: https://leetcode.cn/problems/construct-string-from-binary-tree/description/
整体思路: 这个题本⾝难度不⼤，就是⼀个前序遍历转成字符串，把⼦树⽤括号包起来，空树的情况特殊处理⼀下。这个题⽬就不适合⽤c语⾔去实现，c实现符数组开多⼤就是⿇烦事，⽤C++string的+=就⽅便了很多。
递归子问题: 一棵树字符串 = 左子树字符串 + 右子树字符串.

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void _tree2str(TreeNode* root, string& str){if(!root) return;str += to_string(root->val);if(root->left || (!root->left && root->right)){str += '(';_tree2str(root->left, str);str += ')';}if(root->right){str += '(';_tree2str(root->right, str);str += ')';}return;}string tree2str(TreeNode* root) {string ret;_tree2str(root, ret);return ret;}
};

T8: 二叉树的层序遍历以及层序遍历2

题目链接: https://leetcode.cn/problems/binary-tree-level-order-traversal/
整体思路:

思路1: 双队列 -> 第一个队列存放结点的指针, 另一个队列存放对应结点的层数
思路2: 一个队列 + 变量 -> 第一个队列存放结点的指针, 另一个变量来记录每层的个数

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {if(root == nullptr) return vector<vector<int>>();vector<vector<int>> ret;queue<TreeNode*> q;int leveSize = 0;q.push(root);while(!q.empty()){leveSize = q.size();vector<int> t;while(leveSize--){TreeNode* front = q.front(); //这个地方不小心把变量名和函数名写成一个名字了, 尽量还是不要一个名字q.pop();t.push_back(front->val);if(front->left) q.push(front->left);if(front->right) q.push(front->right);}ret.push_back(t);}return ret;}
};

这个层序遍历除了上面说的之外, 实际上还有一个类似的题目:
题目链接: https://leetcode.cn/problems/binary-tree-level-order-traversal-ii/description/
整体思路: 与上类似.

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> vv;if(root == nullptr){return vv;}queue<TreeNode*> q_p;int leveSize = 0;q_p.push(root);while(!q_p.empty()){leveSize = q_p.size();vector<int> v;while(leveSize--){TreeNode* node = q_p.front();v.push_back(node->val);q_p.pop();if(node->left) q_p.push(node->left);if(node->right) q_p.push(node->right);}vv.push_back(v);}reverse(vv.begin(), vv.end());return vv;}
};

T9: 二叉树的最近公共祖先

题目链接: https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/description/
整体思路: 这个题目有两个思路

思路1: 规律: 对于最近公共祖先来说, 他的一个孩子在左边, 一个孩子在右边其中, 第二种情况算是一种特殊情况其他祖先都不满足这个规律, 只有最近公共祖先才满足这个规律~
思路2: 如果能求出两个结点到根的路径，那么就可以转换为链表相交问题。如：6到根3的路径为6->5->3，4到根3的路径为4->2->5->3，那么看做两个链表找交点，交点5就是最近公共祖先。

下面我们依次来简单说一下这两个思路吧~
首先这个思路1, 就是去卡规律来找公共祖先的, 你看, 假如我们找4和6的公共祖先.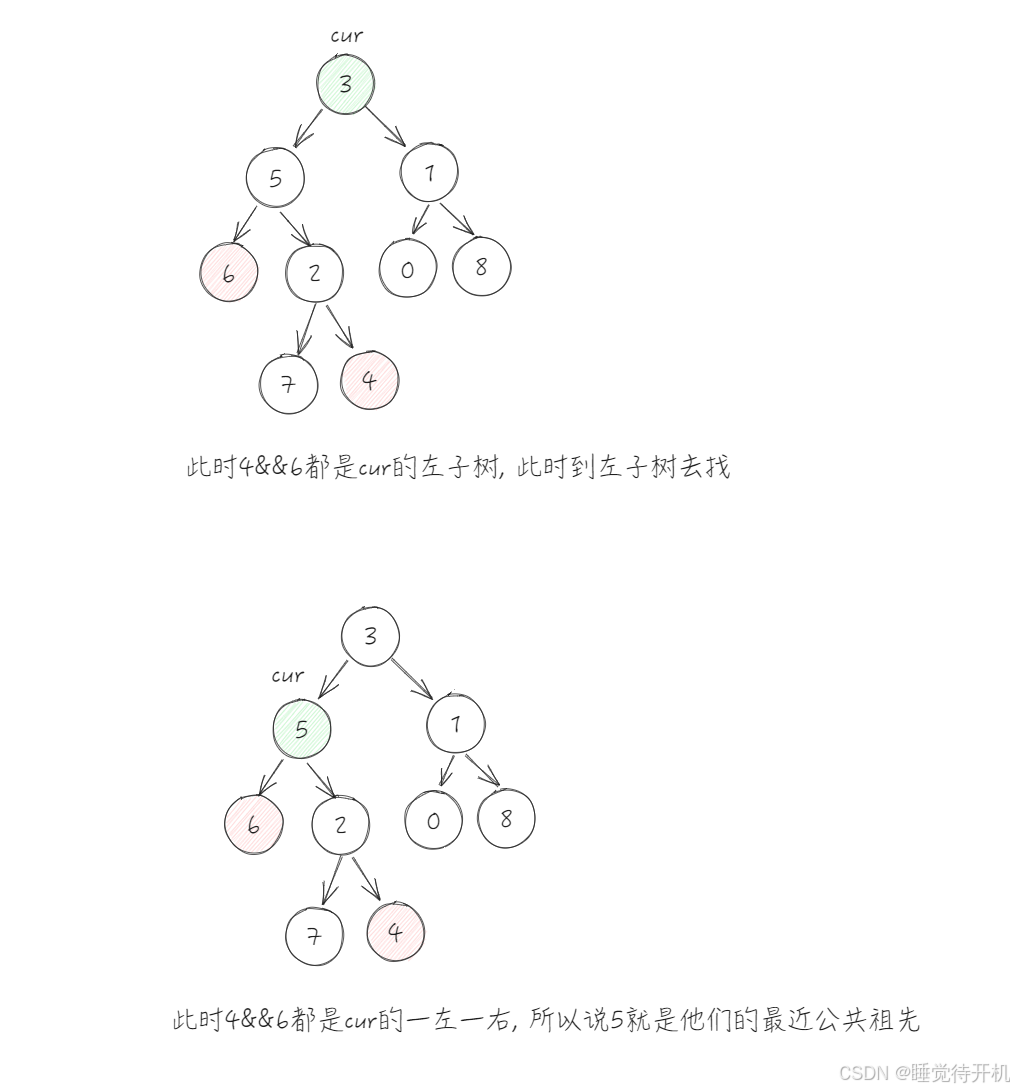 在这里插入图片描述

ok, 咱们就按照这个思路去写一下代码.

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:bool isInTree(TreeNode* root, TreeNode* node){if(root == nullptr) return false;if(root->val == node->val) return true;return isInTree(root->left, node) || isInTree(root->right, node);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(!root) return nullptr; //这个纯属是为了让编译器编过if(root->val == q->val || root->val == p->val) return root; //如果根就是q或者p, 那么这个根就是最近公共祖先bool pInLeft = isInTree(root->left, p);bool pInRight = !pInLeft;bool qInLeft = isInTree(root->left, q);bool qInRight = !qInLeft;//cout << pInLeft << endl << qInLeft << endl; //调试信息if(pInLeft && qInRight || pInRight && qInLeft) //如果一左一右, 直接返回. {return root;}else if(pInLeft && qInLeft) //如果都在左边, 去左子树找. {return lowestCommonAncestor(root->left, p, q);}else if(pInRight && qInRight) //如果都在右边, 去右子树找. {return lowestCommonAncestor(root->right, p, q);}else //方便调试{cout << "unknown mistake" << endl;}return nullptr; //照顾编译器编过}
};

但是这种时间复杂度是O(N*N), 效率不太高~
在这里插入图片描述

下面我们来分享第二种思路:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:bool getPath(stack<TreeNode*>& st, TreeNode* root, TreeNode* x){if(root == nullptr) return false;st.push(root); //先无脑入栈if(root->val == x->val) return true; //如果找到了, 就返回trueif(getPath(st, root->left, x)) return true; //如果再左边找到了, 就返回trueif(getPath(st, root->right, x)) return true; //如果在右边找到了, 就返回truest.pop(); //左右都没有找到? 没关系, pop掉数据, 然后返回false, 让他去其他路径找~ return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*> pst;stack<TreeNode*> qst;getPath(pst, root, p);getPath(qst, root, q);// while(!pst.empty())// {//     cout << pst.top()->val << " ";//     pst.pop();// }// cout << endl;// while(!qst.empty())// {//     cout << qst.top()->val << " ";//     qst.pop();// }// cout << endl;//比较长的先出数据while(pst.size() != qst.size()){if(pst.size() > qst.size()){pst.pop();}else{qst.pop();}}//继续出数据, 直到找到一样的数据while(pst.top() != qst.top()){pst.pop();qst.pop();}return qst.top();//return nullptr; //调试信息}
};

T10: 将二叉搜索树转换为排序的双向链表

题目链接: https://leetcode.cn/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/description/
整体思路: 记录⼀个cur和prev，cur为当前中序遍历到的结点，prev为上⼀个中序遍历的结点，cur->left指向prev，cur->right⽆法指向中序下⼀个，因为不知道中序下⼀个是谁，但是prev->right指向cur；也就是说每个结点的左是在中遍历到当前结点时修改指向前驱的，但是当前结点的右，是在遍历到下⼀个结点时，修改指向后继的。
下面我们来简单展示一下代码:

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node() {}Node(int _val) {val = _val;left = NULL;right = NULL;}Node(int _val, Node* _left, Node* _right) {val = _val;left = _left;right = _right;}
};
*/
class Solution {
public:void _treeToDoublyList(Node* root, Node*& prev) {if(root == nullptr) return;_treeToDoublyList(root->left, prev); //先访问左子树//在修改对应指向root->left = prev;if(prev) prev->right = root;prev = root;_treeToDoublyList(root->right, prev); //在访问右子树}Node* treeToDoublyList(Node* root) {// 如果该树是空树, 直接返回nullptr即可~ if(root == nullptr) return nullptr;//如果这棵树不是空树, 先找到头Node* head = root;while(head->left){head = head->left;}//然后我们再改变各个结点的指向Node* prev = nullptr;_treeToDoublyList(root, prev); //此时prev恰好就是该树最后一个结点, 然后head是该树第一个结点head->left = prev;prev->right = head;return head; }
};

T11: 从前序与中序遍历中构建二叉树

题目链接: https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
整体思路: 前序的⽅式构建树，前序确定当前构建树的根，根分割中序的左⼦树和右⼦树，再分别递归构建左⼦树和右⼦树。106的题思想跟本体类似，不过是后序倒着确定根，再分别递归构造右⼦树和左⼦树。
参考代码如下:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& previ, int inbegin, int inend){if(inbegin > inend) return nullptr;//制造结点TreeNode* root = new TreeNode(preorder[previ++]);//根分割左右子树int rooti = inbegin;while(rooti <= inend){if(preorder[previ - 1] == inorder[rooti]){break;}rooti++;}//左节点? 右节点? [inbegin, rooti-1] rooti [rooti + 1, inend]root->left = _buildTree(preorder, inorder, previ, inbegin, rooti - 1);root->right = _buildTree(preorder, inorder, previ, rooti + 1, inend);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int previ = 0;return _buildTree(preorder, inorder, previ, 0, inorder.size() - 1);}
};

与之类似的一个题目是让你用后序和中序去构建二叉树:
题目链接: https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/
整体思路: 与上一致.

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& posti, int inbegin, int inend){if(inbegin > inend) return nullptr;//构建根TreeNode* root = new TreeNode(postorder[posti--]);if(root)cout << root->val << endl;elsecout << "nullptr" << endl;//分割左右子树int rooti = inbegin;while(rooti <= inend){if(postorder[posti + 1] == inorder[rooti]){break;}rooti++;}//左子树? 右子树? 注意: 这个地方是先右子树再左子树~ root->right = _buildTree(inorder, postorder, posti, rooti + 1, inend);root->left = _buildTree(inorder, postorder, posti, inbegin, rooti - 1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int i = postorder.size() - 1;return _buildTree(inorder, postorder, i, 0, inorder.size() - 1);}
};

T12: 二叉树的前序/中序/后续遍历(非递归形式)

1. 前序遍历

题目链接: https://leetcode.cn/problems/binary-tree-preorder-traversal/description/
整体思路: 用数据结构的栈模拟系统栈帧建立过程. 如果是左路节点, 那我就入栈入ret结果, 再依次出栈看看每个结点的右子树什么情况.

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {TreeNode* cur = root;stack<TreeNode*> st;vector<int> ret;while(cur || !st.empty()){//入栈, 左路节点while(cur){ret.push_back(cur->val);st.push(cur);cur = cur->left;}//2.在栈中依次去访问左路节点的右子树TreeNode* top = st.top();st.pop();//3.循环子问题cur = top->right;// - 假如说top->right不是空, 那么会继续入这个左节点的右子树的左节点进去// - 假如说是空, 下次循环就不入结点, 而是再去看下一个左路节点的右子树情况, 直到栈为空~ }return ret;}
};

2. 中序遍历

题目链接: https://leetcode.cn/problems/binary-tree-inorder-traversal/description/
整体思路: 用数据结构的栈模拟系统栈帧建立过程. 如果是左路节点, 那我就入栈, 再依次出栈, 出栈的时候入ret结果, 看看每个结点的右子树什么情况.

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {TreeNode* cur = root;stack<TreeNode*> st;vector<int> ret;while(cur || !st.empty()){//入栈, 左路节点while(cur){st.push(cur);cur = cur->left;}//出栈, 看一下左路节点的右子树什么情况TreeNode* top = st.top();ret.push_back(top->val);st.pop();//递归子问题cur = top->right;// - 如果是空, 那我继续看栈里下一个结点的右子树. // - 如果不是空, 那我就入这个右子树. }return ret;}
};

3. 后序遍历

题目链接: https://leetcode.cn/problems/binary-tree-postorder-traversal/description/
整体思路: 左路结点入栈, 然后看看每个左路结点的右子树什么情况, 如果右子树是空, 那我们把根入ret, 如果不是空, 那就先去高右子树, 搞完右子树之后, 我们再入根.
技巧: 如何判断右子树是否入过栈了呢? 我们用一个prev指针记录前一次结点的右子树入过栈的结点地址即可.

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> ret;TreeNode* cur = root;TreeNode* prev = nullptr;while(cur || !st.empty()){while(cur){st.push(cur);cur = cur->left;}TreeNode* top = st.top();if(top->right == nullptr || top->right == prev) //如果右子树是空, 或者右子树已经访问过了, 咱们就直接pop掉根, 然后把根入到ret中. {if(top->right == nullptr){cout << "top->val == " << top->val << " :: ";cout << "top->right == nullptr" << endl;}else{cout << "top->right == " << top->right->val << " " << "prev: " << prev->val << endl;}st.pop();ret.push_back(top->val);prev = top;}else //如果top的右子树存在且没有访问过, 那么我们递归子问题, 入右子树的值进栈. {cout << "top->val == " << top->val << " :: ";cout << "cur = top->right;" << endl;cur = top->right;}}return ret;}
};