概要
二叉搜索树虽可以缩短查找效率,但若数据有序或者接近有序,二叉搜索树将退化为单支树,查找数据相当于在顺序表中搜索,效率底下。
AVL的概念
- AVL树是最先发明的自平衡二叉查找树。它是一颗空树,或者具备下列性质的二叉搜索树:它的左右子树都是AVL树,且左右子树的高度差的绝对值不超过1。AVL树是一颗高度平衡搜索二叉树,通过控制高度差去控制平衡。
- AVL树得名于它的发明者G. M. Adelson - Velsky和E. M. Landis,他们是两个前苏联的科学家,在1962年的论文《An algorithm for the organization of information》中发表了它。
- 引入平衡因子(balance factor)的概念,每个结点都有一个平衡因子,任何结点的平衡因子等于右子树的高度减去左子树的高度,即任何结点的平衡因子等于0、1或 - 1。AVL树并不是必须要平衡因子,但是有了平衡因子可以更方便观察和控制树是否平衡。
- 思考为何AVL树要求高度差不超过1,而不是高度差是0。通过画图分析可知,有些情况做不到高度差是0,比如一棵树是2个结点、4个结点等情况下,高度差最好就是1。
- AVL树整体结点数量和分布和完全二叉树类似,高度可以控制在 (log N) ,那么增删查改的效率也可以控制在 (O(log N)) ,相比二叉搜索树有了本质的提升。
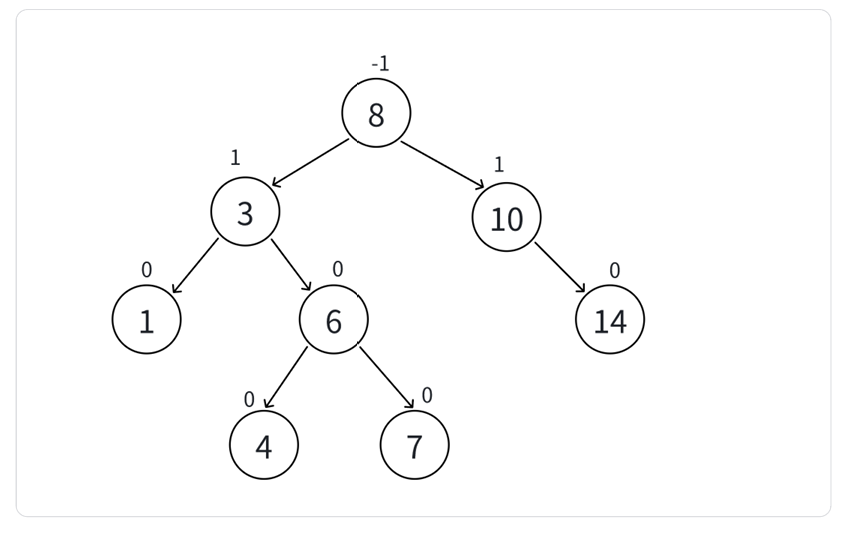
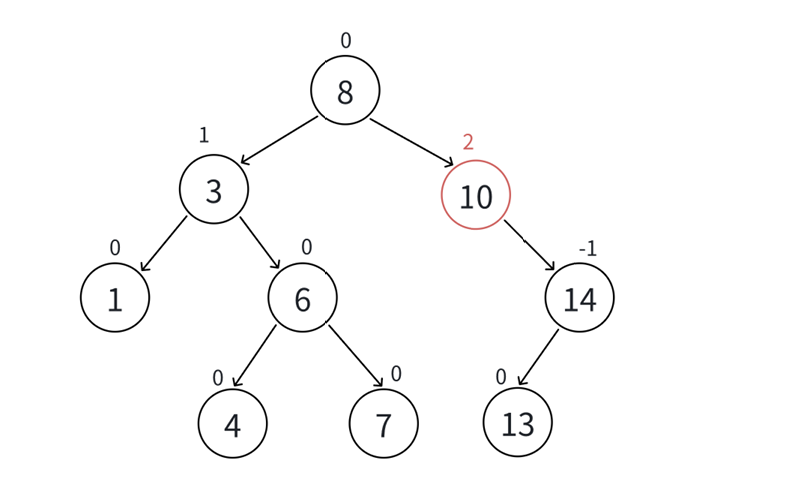
AVL树的实现
- AVL树的结构
template<class K, class V>
struct AVLTreeNode
{// 需要parent指针,后续更新平衡因子可以看到pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public://...
private:Node* _root = nullptr;
};
AVL树的插入
- AVL树插入一个值的大概过程:
- 按二叉搜索树规则进行插入。
- 新增结点后,只会影响祖先结点的高度,可能会影响部分祖先结点的平衡因子,所以更新从新增结点到根结点路径上的平衡因子,最坏情况下要更新到根,有些情况更新到中间就可以停止。
- 更新平衡因子过程中没有出现问题,则插入结束。
- 更新平衡因子过程中出现不平衡,对不平衡子树旋转,旋转后在调平衡的同时,降低了子树的高度,不会再影响上一层,插入结束。
- 平衡因子更新:
- 更新原则:平衡因子 = 右子树高度 - 左子树高度;
- 只有子树高度变化才会影响当前结点平衡因子;
- 插入结点,会增加高度,新增结点在parent的右子树,parent的平衡因子
++,新增结点在parent的左子树,parent平衡因子--; - parent所在子树的高度是否变化决定了是否会继续往上更新。
- 更新停止条件:
-
更新后parent的平衡因子等于0,更新中parent的平衡因子变化为
- 1 -> 0或者1 -> 0:- 说明更新前parent子树一边高一边低,新增的结点插入在低的那边,插入后parent所在的子树高度不变,不会影响parent的父亲结点的平衡因子,更新结束;
-
更新后parent的平衡因子等于1或 - 1,更新前更新中parent的平衡因子变化为
0 -> 1或者0 -> - 1:- 说明更新前parent子树两边一样高,新增的插入结点后,parent所在的子树一边高一边低,parent所在的子树符合平衡要求,但是高度增加了1,会影响parent的父亲结点的平衡因子,所以要继续向上更新;
-
更新后parent的平衡因子等于2或 - 2,更新前更新中parent的平衡因子变化为1 -> 2或者 - 1 -> - 2:
- 说明更新前parent子树一边高一边低,新增的插入结点在高的那边,parent所在的子树高的那边更高了,破坏了平衡,parent所在的子树不符合平衡要求,需要旋转处理:
- 旋转的目标有两个:把parent子树旋转平衡;降低parent子树的高度,恢复到插入结点以前的高度,所以旋转后也不需要继续往上更新,插入结束;
-
不断更新,更新到根,根的平衡因子是1或 - 1也停止了。
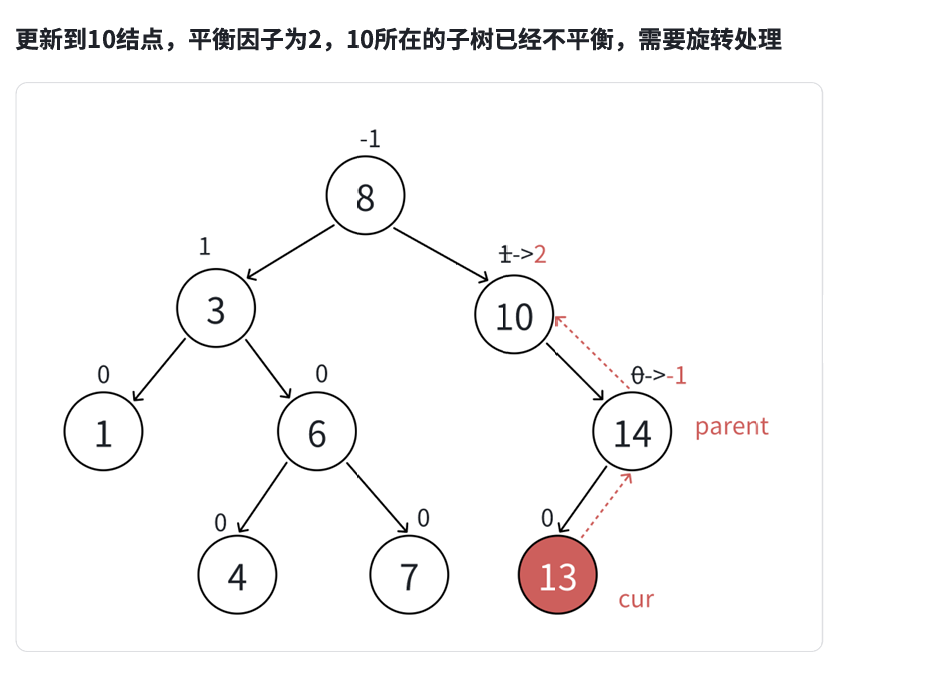
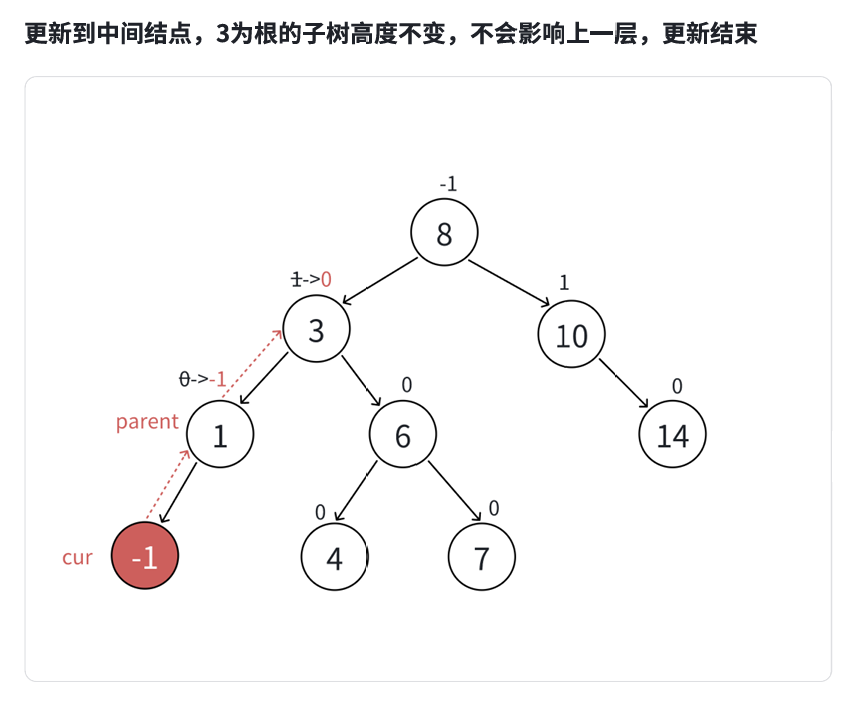
最坏更新到根停止
-
- 更新原则:平衡因子 = 右子树高度 - 左子树高度;
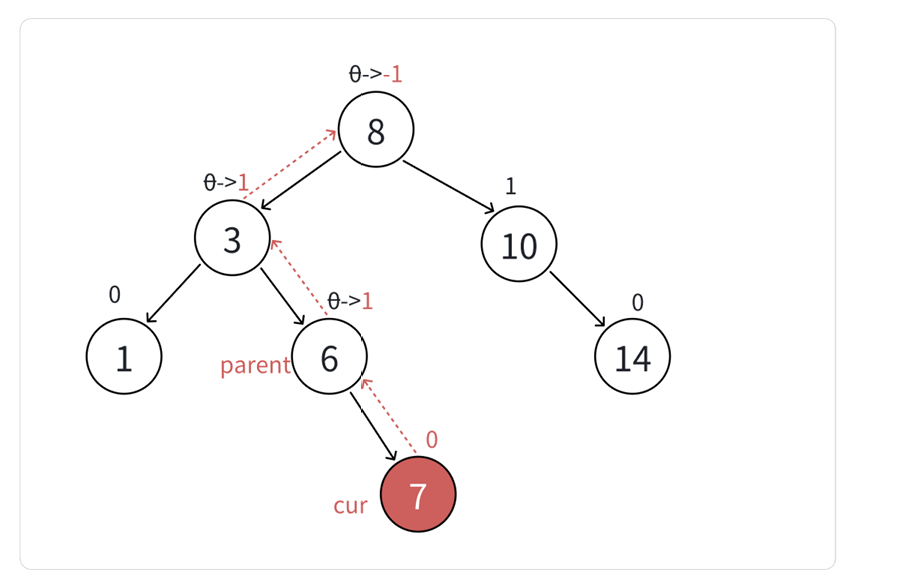
- 插入结点及更新平衡因子的代码实现:
bool Insert(const pair<K,V>&kv)
{if(_root == nullptr){_root = new Node(kv);return true;}Node* parent=nullptr;Node* cur=_root;while (cur){if(cur->_kv.first < kv.first){parent=cur;cur=cur->_right;}else if (cur->_kv.first > kv.first){parent =cur;cur=cur->_left;}else //不允许相同key值插入{return false;}}cur=new Node(kv);if(parent->_kv.first<kv.first){parent->_right=cur;}else{parent->_left =cur;}cur->_parent = parent;//更新平衡因子while (parent){//更新平衡因子if(cur ==parent->_left)parent->_bf--;elseparent->_bf++;if(parent->_bf==0){//更新结束break;}else if(parent->_bf==1||parent->_bf==-1){//继续往上更新cur = parent;parent=parent->_parent;}else if (parent->_bf ==2|| parent->_bf==-2){//不平衡了,旋转处理break;}else{assert(false);}}return true;
}
旋转
- 旋转的原则:
- 保持搜索树的规则;
- 让旋转的树从不满足变平衡,其次降低旋转树的高度。
旋转总共分为四种,左单旋、右单旋、左右双旋、右左双旋。
说明:下面的图中,有些结点我们给的是具体值,如10和5等结点,这里是为了方便寿命,实际中是什么值都可以,只要大小关系符合搜索树的性质即可。
右单旋
- 在a子树中插入一个新结点,导致a子树的高度从h变成h+1,不断向上更新平衡因子,导致10的平衡因子从-1变成-2,10为根的树左右高度差超过1,违反平衡规则。10为根的树左边太高了,需要往右边旋转,控制两棵树的平衡。
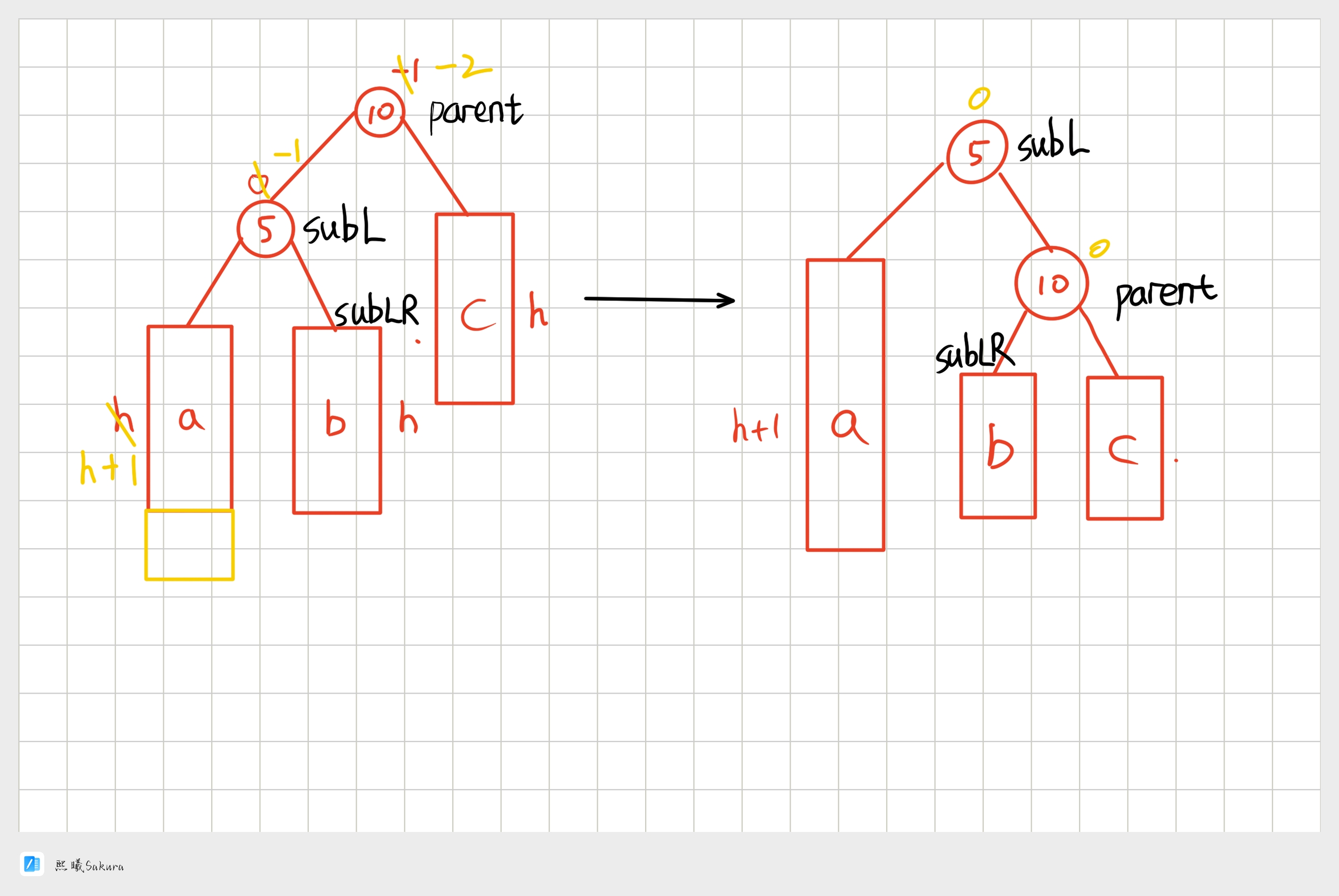
-
旋转核心步骤:
- 因为
5< b子树的值 <10,将b变成10的左子树,10变成5的右子树,5变成这棵树新的根,符合搜索树的规则,控制了平衡,同时这棵的高度恢复到了插入之前的h+2,符合旋转原则。如果插入之前10整棵树的一个局部子树,旋转后不会再影响上一层,插入结束了。
- 因为
-
右单旋代码实现:
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;// 需要注意除了要修改孩子指针指向,还是修改父亲parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;// parent有可能是整棵树的根,也可能是局部的子树// 如果是整棵树的根,要修改_root// 如果是局部的指针要跟上一层链接if (parentParent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (parent == parentParent->_left)parentParent->_left = subL;elseparentParent->_right = subL;subL->_parent = parentParent;}parent->_bf = subL->_bf = 0;
}
左单旋
- 旋转核心步骤:
- 因为
10<b子树的值<15,将b变成10的右子树,10变成15的左子树,15变成这棵树新的根,符合搜索树的规则,控制了平衡,同时这棵的高度恢复到了插入之前的h+2,符合旋转原则。如果插入之前10整棵树的一个局部子树,旋转后不会再影响上一层,插入结束了。
- 因为
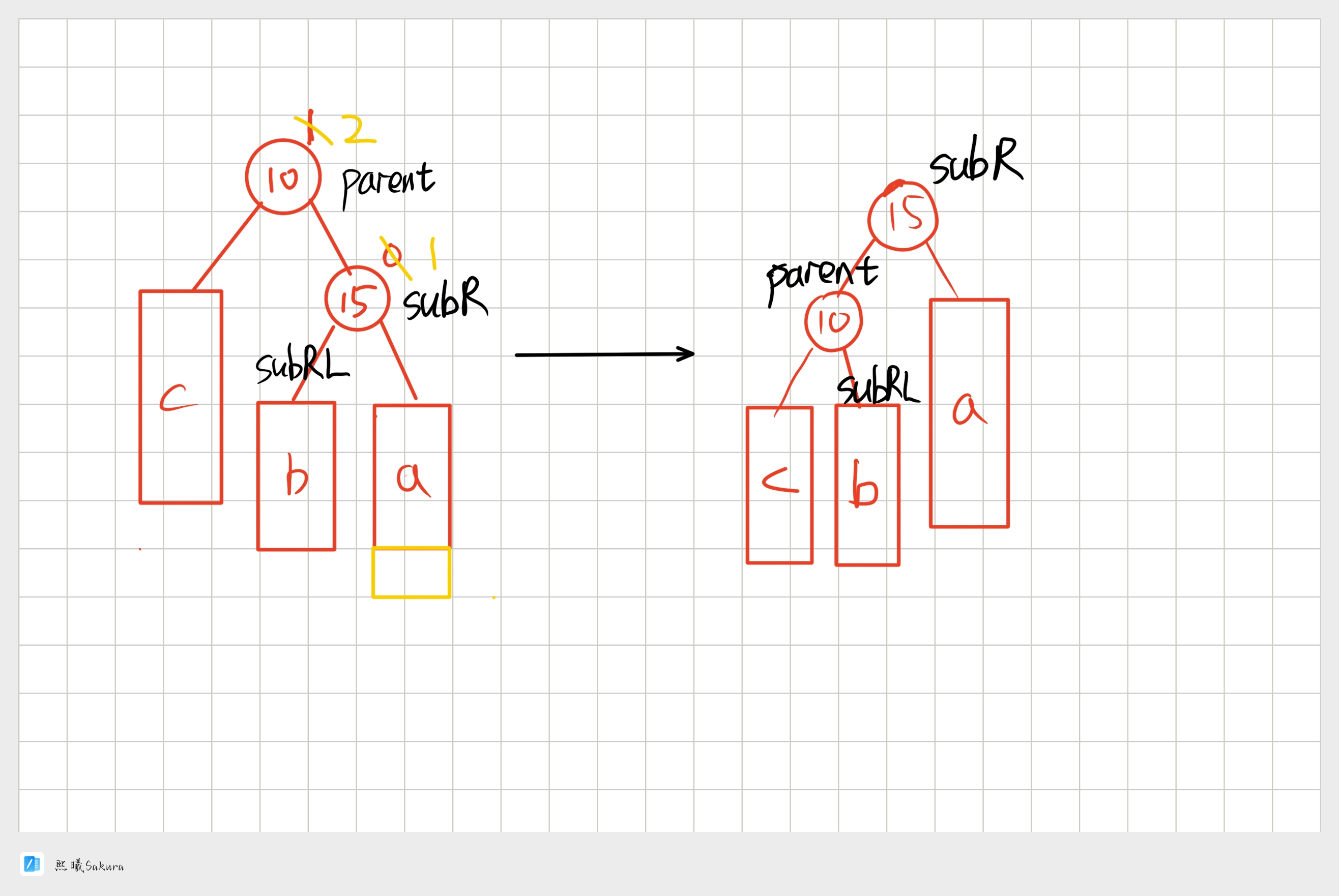
- 左单旋代码实现:
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if(subRL)subRL->_parent = parent;Node* parentParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parentParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (parent == parentParent->_left)parentParent->_left = subR;elseparentParent->_right = subR;subR->_parent = parentParent;}parent->_bf = subR->_bf = 0;
}
左右双旋
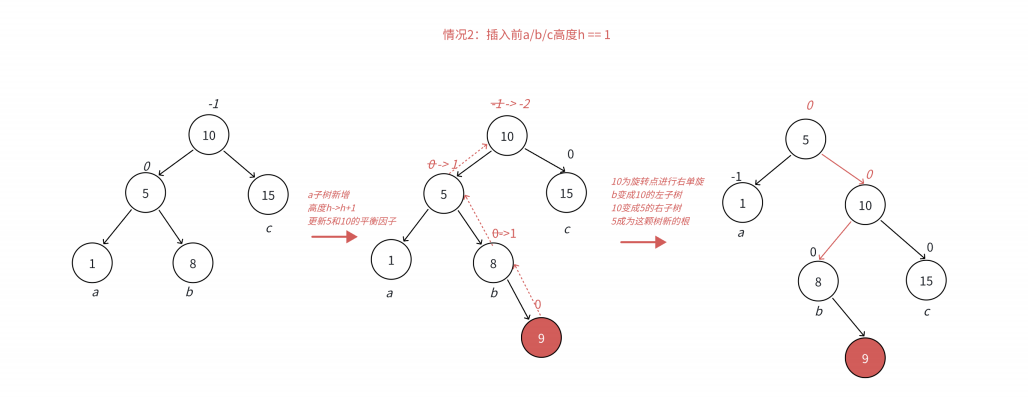
通过图7和图8可以看到,左边高时,如果插入位置不是在a子树,而是插入在b子树,b子树高度从h变 成h+1,引发旋转,右单旋无法解决问题,右单旋后,我们的树依旧不平衡。
**右单旋解决的纯粹的左边高,**但是插入在b子树中,10为跟的子树不再是单纯的左边高,对于10是左边高,但是对于5是右边 高,需要用两次旋转才能解决,以5为旋转点进行一个左单旋,以10为旋转点进行一个右单旋,这棵树 这棵树就平衡了。
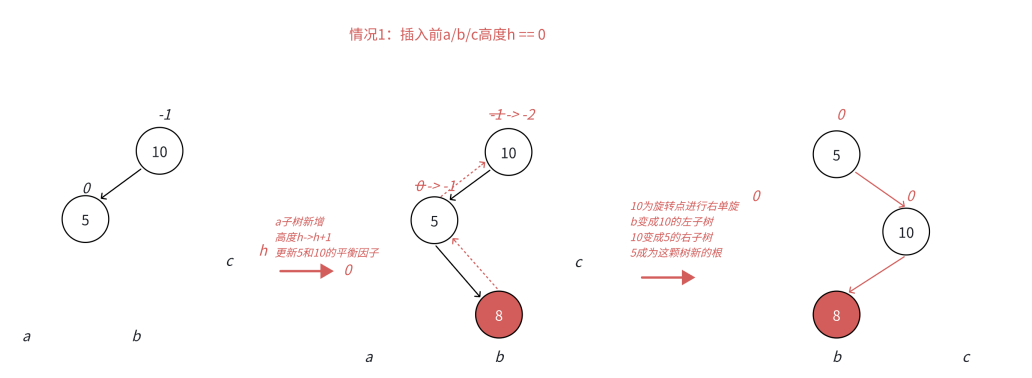
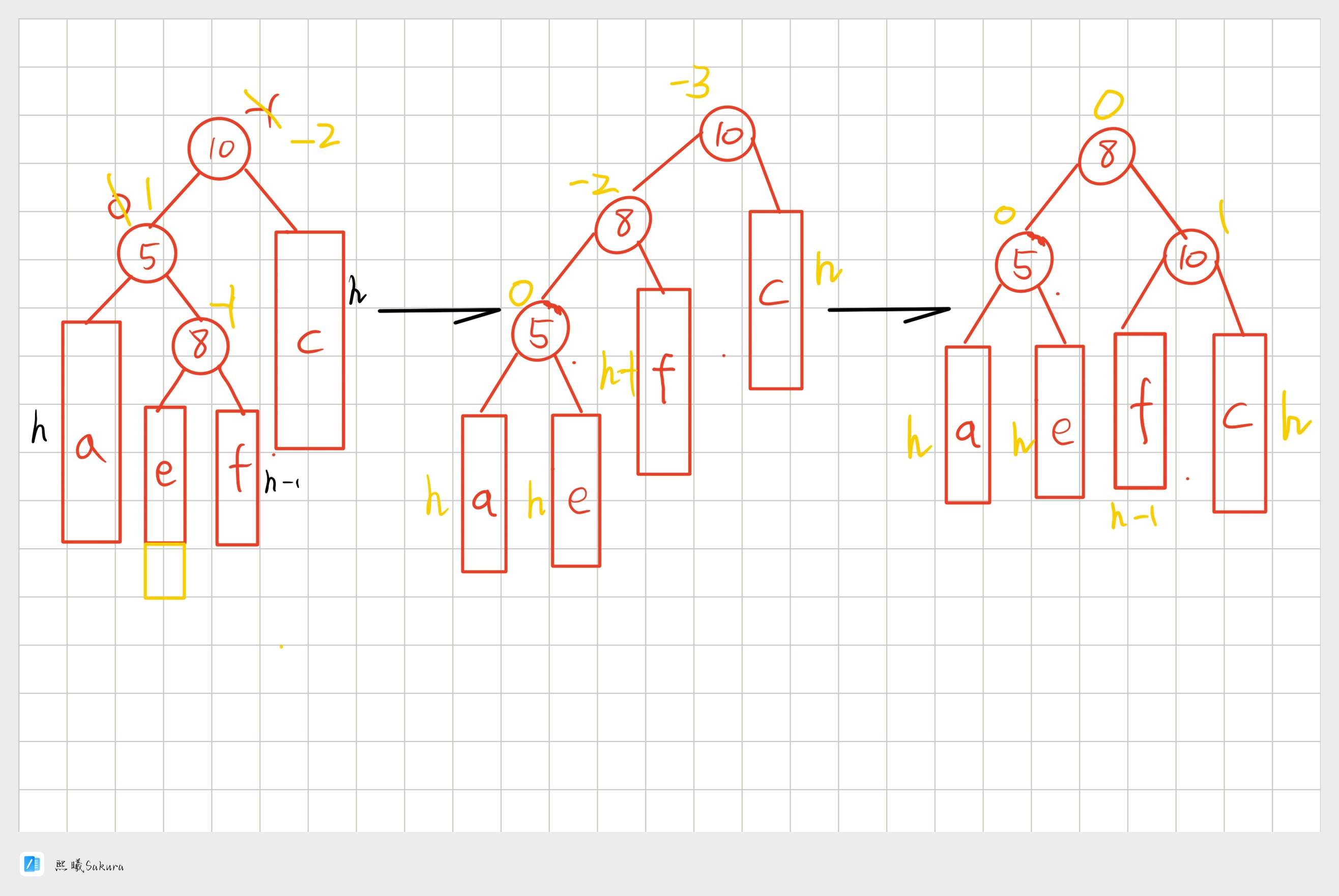
下面我们将a/b/c子树抽象为高度h的AVL子树进行分析,另外我们需要把b子树的细节进一步展开为左右子树高度为h-1的e和f子树,因为我们要对b的父亲5为旋转点进行左单旋,左单旋需要动b树中的左子树。
b子树中新增结点的位置不同,平衡因子更新的细节也不同,通过观察8的平衡因子不同,这里我们要分三个场景讨论。
- 场景1: (h>=1) 时,新增结点插入在e子树,e子树高度从h-1并为h并不断更新 (8->5->10) 平衡因子, 引发旋转,其中8的平衡因子为-1,旋转后8和5平衡因子为0,10平衡因子为1。
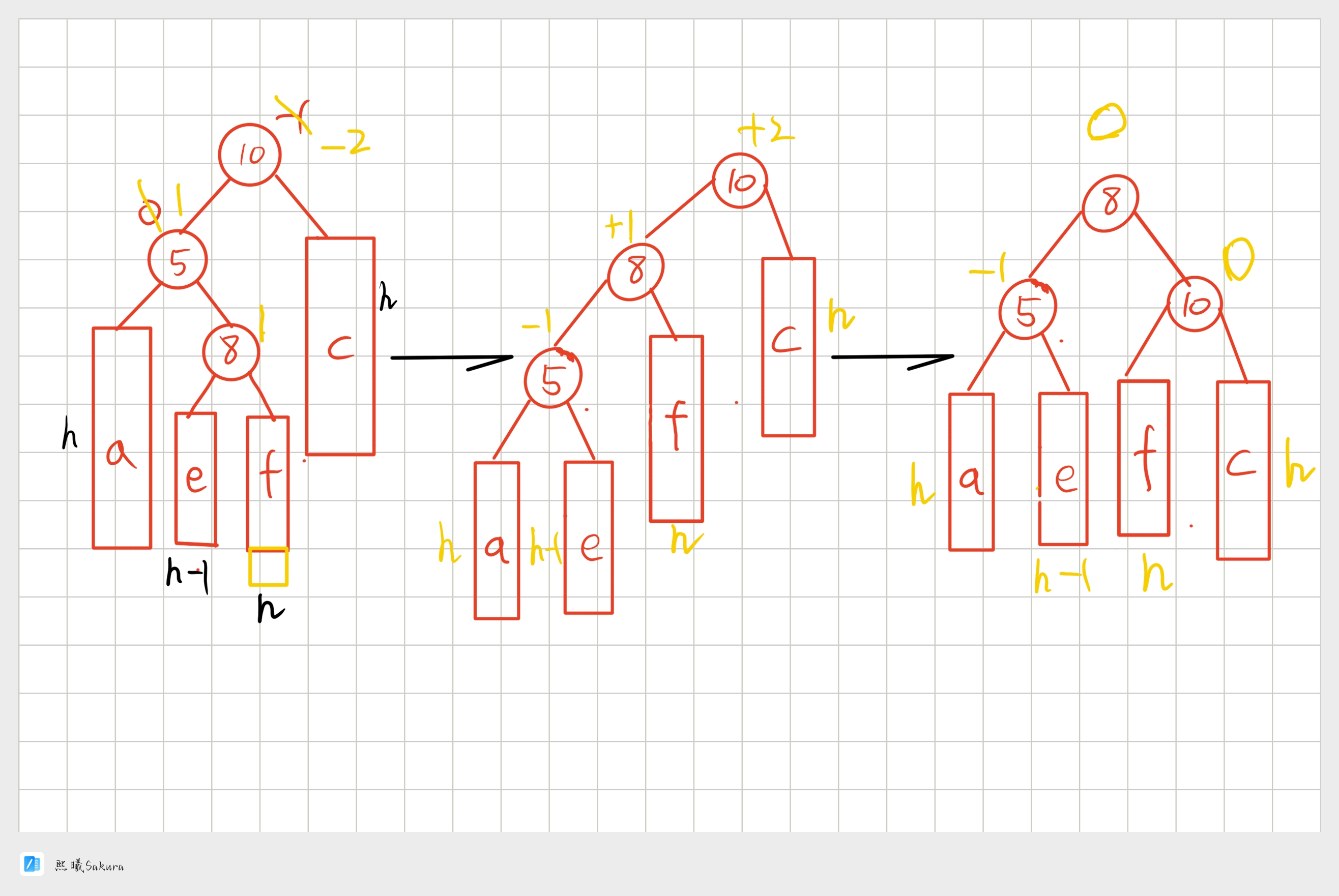
- 场景2: (h>=1) 时,新增结点插入在f子树,f子树高度从h-1变为h并不断更新 (-8->5->10) 平衡因子,引 发旋转,其中8的平衡因子为1,旋转后8和10平衡因子为0,5平衡因子为-1。
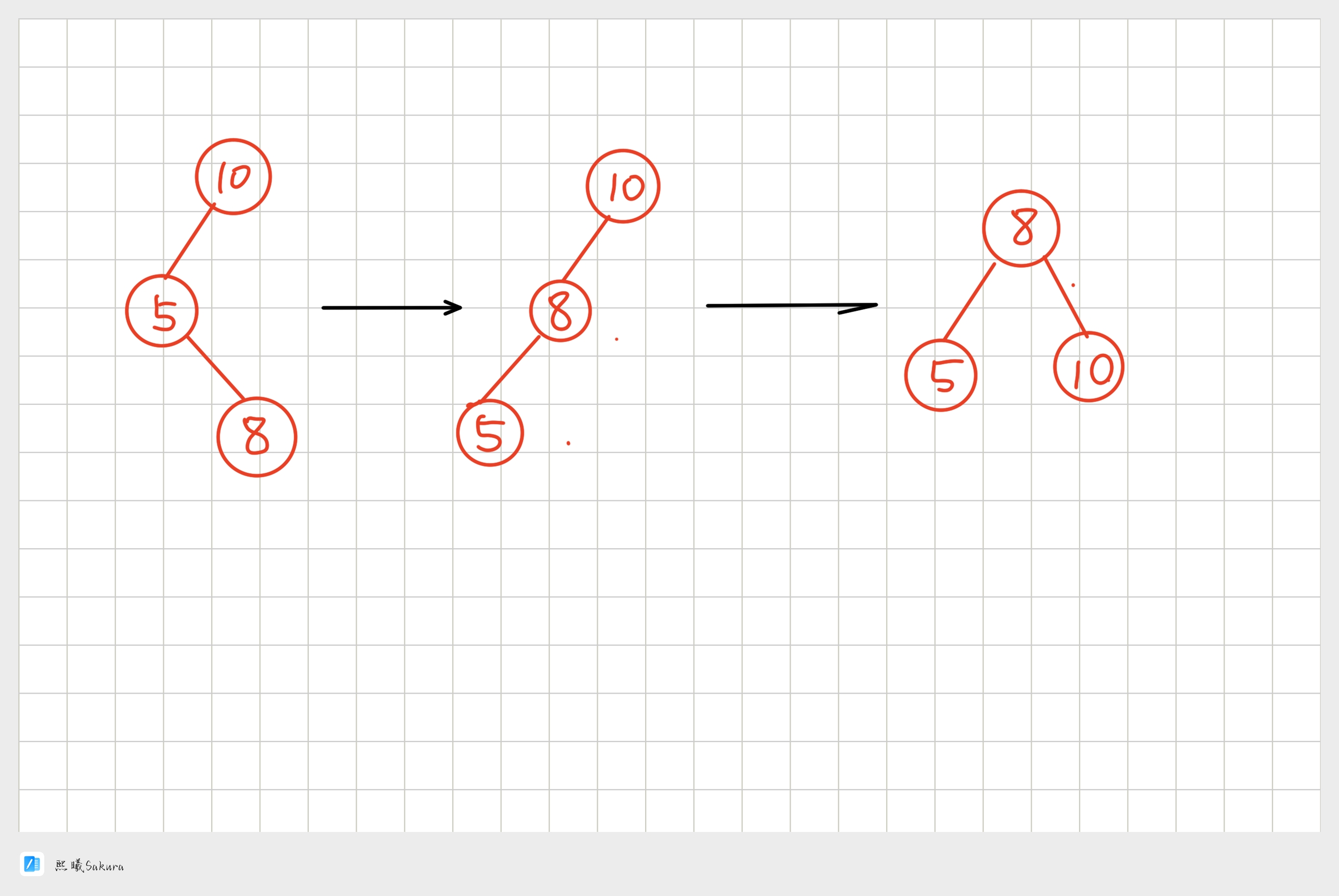
-
场景3: (h==0) 场景3:h == 0时,a/b/c都是空树,b自己就是一个新增结点,不断更新5->10平衡因子,引发旋 转,其中8的平衡因子为0,旋转后8和10和5平衡因子均为0。
-
左右双旋代码实现:
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if(bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else{assert(false);}
}
右左双旋
- 跟左右双旋类似,对b子树的细节展开,分不同场景讨论b子树中新增结点的位置对平衡因子的影响,通过两次旋转(先右单旋后左单旋)使树平衡。
- 右左双旋代码实现:
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}
AVL树的查找
按二叉搜索树逻辑实现即可,搜索效率为 (O(log N)) 。
Node* Find(const K& key)
{Node* cur = _root;while (cur){if(cur->_kv.first<key){cur = cur->_right;}else if (cur->_kv.first>key){cur=cur->_left;}else{return cur;}}return nullptr;
}
AVL树平衡检测
通过检查左右子树高度差的程序进行反向验证,同时检查结点的平衡因子更新是否出现问题。
int _Height(Node* root)
{if (root ==nullptr)return 0;int LeftHeight=_Height(root->_left);int rightheight =_Height(root->_right);return LeftHeight>rightHeight? leftHeight + 1:rightHeight + 1;
}bool _IsBalanceTree(Node* root)
{//空树也是AVL树if(nullptr == root)return true;//计算pRoot结点的平衡因子:即pRoot左右子树的高度差int LeftHeight=_Height(root->_left);int rightHeight =_Height(root->_right);int diff = rightheight - leftHeight;// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者// pRoot平衡因子的绝对值超过1,则一定不是AVL树if (abs(diff) >= 2){cout << root->_kv.first << "高度差异常" << endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子异常" << endl;return false;}// pRoot的左和右如果都是AVL树,则该树一定是AVL树return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}// 测试代码
void TestAVLTree1()
{AVLTree<int, int> t;// 常规的测试用例//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// 特殊的带有双旋场景的测试用例int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){t.Insert({ e, e });}t.InOrder();cout << t.IsBalanceTree() << endl;
}// 插入一堆随机值,测试平衡,顺便测试一下高度和性能等
void TestAVLTree2()
{const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand()+i);}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();cout << "Insert:" << end2 - begin2 << endl;cout << t.IsBalanceTree() << endl;cout << "Height:" << t.Height() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 确定在的值/*for (auto e : v){t.Find(e);}*/// 随机值for (size_t i = 0; i < N; i++){t.Find((rand() + i));}size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;
}
- AVL树的删除:本章节不做讲解,有兴趣的同学可参考:《殷人昆数据结构:用面向对象方法与C++语言描述》中讲解。














