原题链接:2209. 用地毯覆盖后的最少白色砖块
题目描述:
给你一个下标从 0 开始的 二进制 字符串 floor ,它表示地板上砖块的颜色。
floor[i] = '0'表示地板上第i块砖块的颜色是 黑色 。floor[i] = '1'表示地板上第i块砖块的颜色是 白色 。
同时给你 numCarpets 和 carpetLen 。你有 numCarpets 条 黑色 的地毯,每一条 黑色 的地毯长度都为 carpetLen 块砖块。请你使用这些地毯去覆盖砖块,使得未被覆盖的剩余 白色 砖块的数目 最小 。地毯相互之间可以覆盖。
请你返回没被覆盖的白色砖块的 最少 数目。
示例 1:

输入:floor = "10110101", numCarpets = 2, carpetLen = 2 输出:2 解释: 上图展示了剩余 2 块白色砖块的方案。 没有其他方案可以使未被覆盖的白色砖块少于 2 块。
示例 2:

输入:floor = "11111", numCarpets = 2, carpetLen = 3 输出:0 解释: 上图展示了所有白色砖块都被覆盖的一种方案。 注意,地毯相互之间可以覆盖。
提示:
1 <= carpetLen <= floor.length <= 1000floor[i]要么是'0',要么是'1'。1 <= numCarpets <= 1000
解题思路:
首先这个题目很容易想到dp,然后来看看怎么找到合适的状态转移方程呢。
首先我们可以定义如下状态转移方程:
f[i][j]表示处理完前i个位置并且以第i个位置结尾,并且当前有j条地毯可以拿来使用时,无法被覆盖到的白色砖块的最小数量。状态转移:
当前位置为i,并且当前有j条地毯。
1.当前位置i不铺地毯,那么留给前i-1个位置的地毯数量为j,那么状态转移方程如下:
f[i][j] = f[i - 1][j] + (floor[i - 1] == '1');
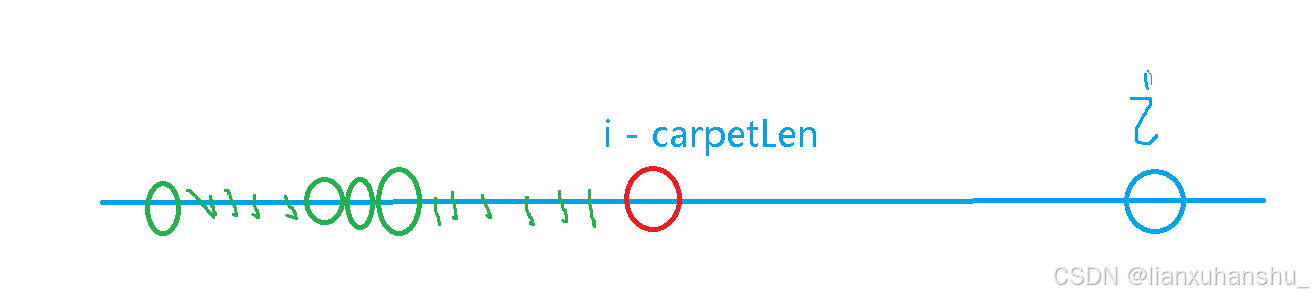
2.当前位置铺地毯,那么留给前面的可以使用的地毯数量为j - 1, 那么我们此时需要知道的就是上一条地毯铺设的位置是哪个位置,最简单的方法是直接枚举上一条地毯铺设的位置,但是这样枚举会带来O(n)的时间,那么前面还需要枚举位置和当前可供使用的地毯数,那么时间为O(nm),那么总的时间为O(n*n*m),n和m最大是1000,那么时间会达到1e9,这样做会超时,那么我们考虑优化,其实上一条地毯铺设的情况会有两种,我们画一个图来描述一下:
如上图所示,当前位置为i,那么如果我们在位置i铺设一条地毯,那么这条地毯最远能覆盖到的位置是i - carpetLen + 1, 也就是红色圈的右边那个位置。
(1)如果上一条地毯铺设的位置在红色圈以及红色圈的右边,那么中间的位置都会被覆盖到,可以发现对于任意一个位置,这一段的长度是固定的,由于我们要求的是最小值,所以我们进行状态转移的时候,实际上需要的是这一段的某个最小值,所以实际上就是求一个长度为carpetLen的滑动窗口内的最小值,这个我们可以使用单调队列进行维护。
(2)如果上一条地毯铺设的位置在红色圈的左边,也就是红色圈的左边某个绿色圈,那么在红色圈和绿色圈之间会有某些白色砖块无法被覆盖到,我们状态转移的时候,肯定需要知道中间有多少个没有被覆盖到的白色砖块,我们可以弄一个数组cnt,其中cnt[i]表示前i个位置中白色砖块的数量,那么中间有多少没有被覆盖的白色砖块就可以使用前缀和来处理,经过我们上面的分析,我们的上一个位置不能一个一个的去枚举,所以我们得考虑优化,从上图我们可以看出来,绿色圈也就是上一个位置实际上是从最前面开始的一段前缀,所以我们可以处理一个前缀g数组来维护前缀最小,定义我们的g[i][j] = min(g[i - 1][j], f[i][j] - cnt[i]),那么我们更新就是f[i][j] = min(f[i][j], cnt[i - carpetLen] + g[i - carpetLen][j - 1]),通过这俩个方程式可以发现,中间没有被覆盖到的白色砖块通过前面的g数组减去了一个前面的部分,又加上一个后面的部分,那么得到的就是中间没有被覆盖到的白色砖块的数量,这样就通过维护前缀最小的方式把枚举上一个位置的时间从O(n)优化到了O(1)。
那么通过上述两种方式,就把这两种情况的枚举上一个铺设地毯位置的时间从O(n)优化到了O(1),此时可以通过此题。
时间复杂度:O(n*m),其中n表示二进制字符串floor的长度,m表示可以拿来使用的地毯的数量。
空间复杂度:O(n*m),其中n表示二进制字符串floor的长度,m表示可以拿来使用的地毯的数量。
cpp代码如下:
const int N = 1010;
int f[N][N], g[N][N];
int q[N][N];
int hh[N], tt[N];
int cnt[N];
class Solution {
public:int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {int n = floor.size();for (int j = 0; j <= numCarpets; j++)hh[j] = 0, tt[j] = -1;// 处理前单调队列,首先把位置0加入for (int j = 0; j <= numCarpets; j++){tt[j]++;q[j][tt[j]] = 0;}for (int i = 1; i <= n; i++)for (int j = 0; j <= numCarpets; j++)f[i][j] = g[i][j] = 1e9;// 预处理前缀1的数量for (int i = 1; i <= n; i++){cnt[i] = cnt[i - 1];if (floor[i - 1] == '1')cnt[i]++;}for (int i = 1; i <= n; i++){for (int j = 0; j <= numCarpets; j++){// 当前位置不铺设地毯f[i][j] = f[i - 1][j] + (floor[i - 1] == '1');if (j >= 1){// 维护滑动窗口的长度,把左边不在窗口内的弹出while (hh[j - 1] <= tt[j - 1] && q[j - 1][hh[j - 1]] < i - carpetLen)hh[j - 1]++;// 用滑动窗口内的最小值进行更新f[i][j] = min(f[i][j], f[q[j - 1][hh[j - 1]]][j - 1]);if (i >= carpetLen){// 用前缀最小进行更新f[i][j] = min(f[i][j], cnt[i - carpetLen] + g[i - carpetLen][j - 1]);}}// 更新滑动窗口while (hh[j] <= tt[j] && f[q[j][tt[j]]][j] >= f[i][j])tt[j]--;tt[j]++;q[j][tt[j]] = i;// 处理g数组,维护前缀最小g[i][j] = min(g[i - 1][j], f[i][j] - cnt[i]);}}return f[n][numCarpets];}
};