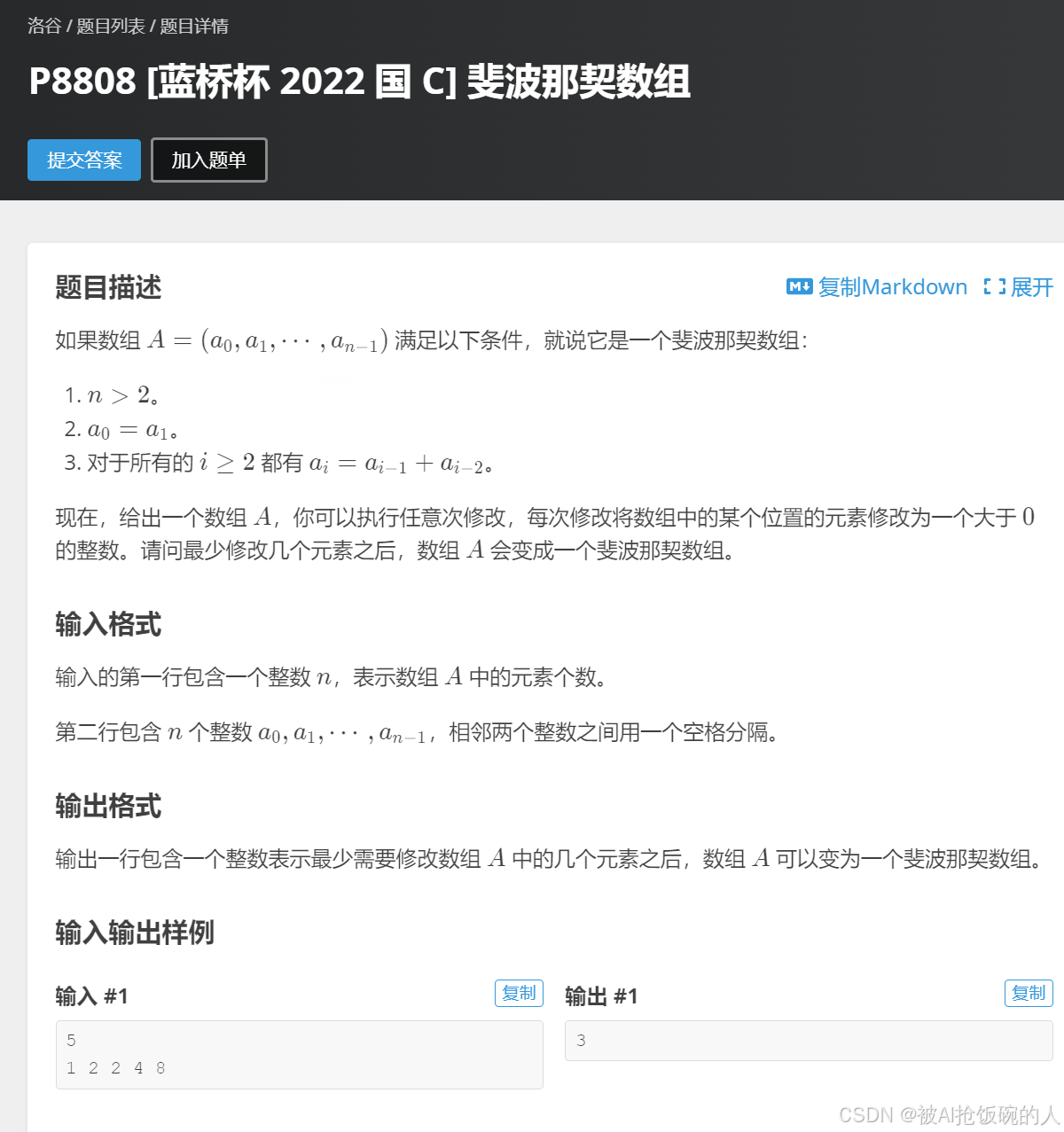
审题:
这题要求我们找到与给定数组相差最少的斐波那契数组的差别数
思路:
我们采用枚举法,把所有的斐波那契数组都枚举出来(从1-1e6),然后与a数组每个元素依次比较,发现不同就让cou++,最后输出最小的cou即可
不过实际上我们只需要枚举出前三十项并比较前三十项就可以了,后面的数据一定会超过斐波那契数组。
我们根据以下两点讲解为什么会这样
(1)给定的数组元素最大为1e6(表示10的6次方)
(2)斐波那契数组元素相当于F(i)*e(这里的F(i)就是前两项都为1的最小的斐波那契数组,e表示a[0]的值,因为所有元素都相当于基础款斐波那契数组乘上一个由前两项决定的倍数)
而最小的斐波那契数组在第三十项的时候会大于1e6(所以我们的其他斐波那契数组在第三十项也一定会大于1e6),故我们只需要求出前三十项的斐波那契数组并和a数组比就可以了
图解:
解题:
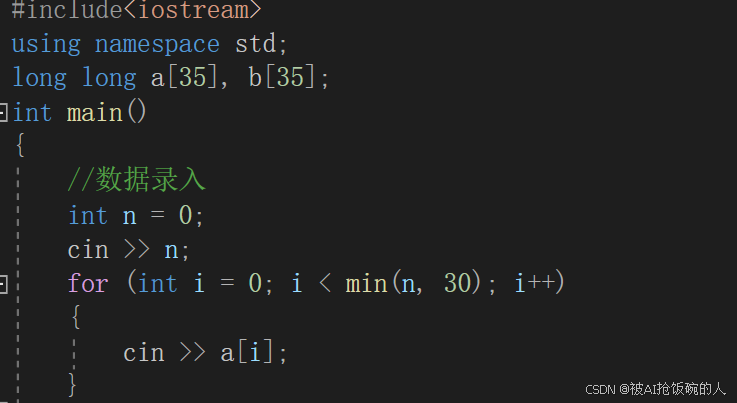
(1)数据录入
由于我们只需要比较前三十位,所以只需要录入前三十项数据即可
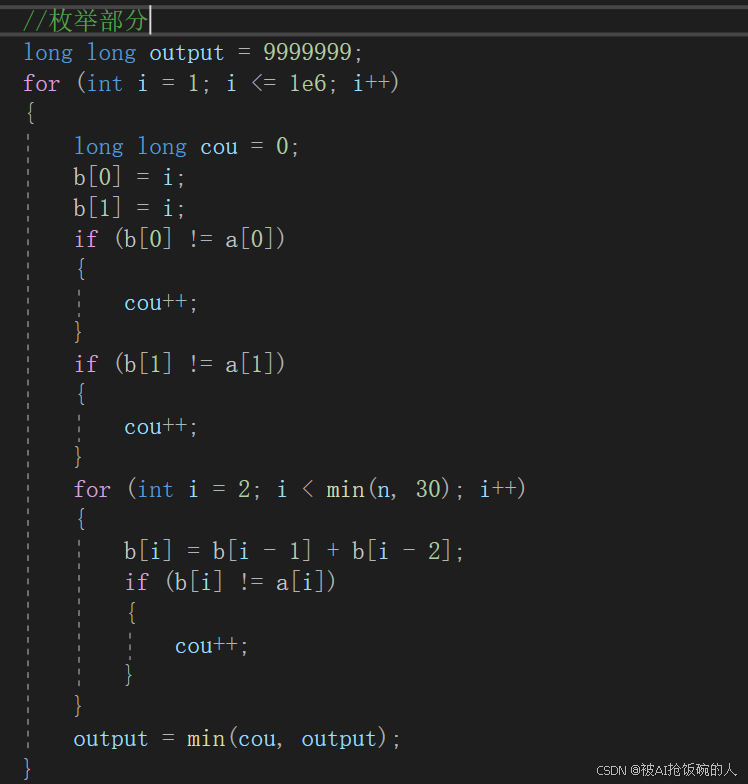
(2)枚举部分
注意:
(1)把cou定义在循环内部:为了清空cou中关于上一次循环的值。
当然也可以定义在外面,然后在开头把它赋值为0
(2)output:用来记录所有情况中最小的次数。
min内部的cou表示当前的次数,output表示目前历史记录中最小的次数
(3)最终处理
当n>=30的时候我们需要把后面的所有数据的次数都加上(因为后面的数据一定是和斐波那契数组不一样的)
[蓝桥杯 2022 国 C] 斐波那契数组 - 洛谷
反思:
1.第一次做的时候我想当然得认为只有两种情况了,我默认需要根据给定的a[0]或者a[1]的值去写斐波那契数组,没有考虑到斐波那契数组的前两个数据都和a的前两个不一样的时候也可能是最小次数