不免费的网络营销方式_百度关键词优化手段_可以免费推广的平台_站长工具seo推广

题目

题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

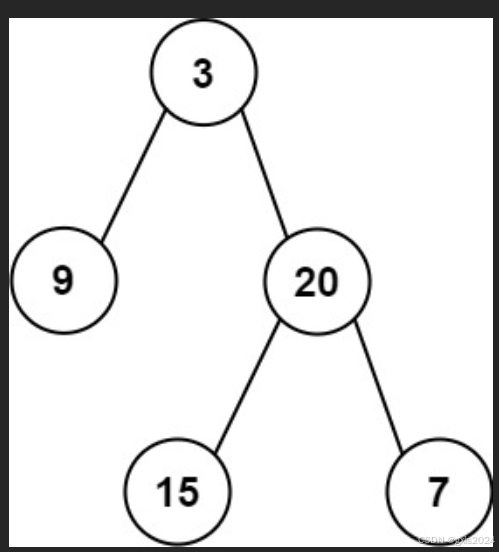
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列

题解

解题思路

要根据给定的前序遍历和中序遍历数组构造二叉树，可以采用递归的方法。基本思路是：

1. 前序遍历的第一个元素总是当前树或子树的根节点。
2. 在中序遍历数组中找到这个根节点的位置，这样就可以知道左子树和右子树的所有节点（所有在根节点左侧的值属于左子树，右侧的属于右子树）。
3. 对于左子树和右子树，重复上述过程，直到构建出整棵树。

python实现

以下是Python代码实现：

def buildTree(preorder, inorder):if not preorder or not inorder:return None# 前序遍历的第一个元素是根节点root_val = preorder[0]root = TreeNode(root_val)# 找到根节点在中序遍历中的位置root_index_in_inorder = inorder.index(root_val)# 递归构建左子树和右子树root.left = buildTree(preorder[1:1 + root_index_in_inorder], inorder[:root_index_in_inorder])root.right = buildTree(preorder[1 + root_index_in_inorder:], inorder[root_index_in_inorder + 1:])return root

代码解释

• TreeNode类：定义了二叉树节点的数据结构。
• buildTree函数：
  • 首先检查preorder和inorder是否为空，若为空则返回None。
  • 取出preorder的第一个元素作为当前树或子树的根节点。
  • 在inorder数组中查找该根节点的位置，以此来确定左右子树的范围。
  • 递归地对左右子树进行相同的操作，直到构建完成整个树。
• printTree函数：用于层次遍历输出构造的二叉树，便于验证结果。

这种方法利用了前序遍历和中序遍历的特点，通过递归的方式有效地重建原始二叉树。时间复杂度主要由查找根节点在中序数组中的位置决定，为O(n^2)最坏情况下（当树退化成链表时）。为了优化查找效率，可以使用哈希表记录每个值在中序数组中的索引，从而将查找操作的时间复杂度降低至O(1)，整体算法的时间复杂度可优化为O(n)。

提交结果