一、贝叶斯原理

二、概率密度函数值

三、协方差计算

四、设计思路
4.1、散点输入
import numpy as np
x1= np.array([[1.9,1.2],[1.5,2.1],[1.9,0.5],[1.5,0.9],[0.9,1.2],[1.1,1.7],[1.4,1.1]])
x2=np.array([[3.2,3.2],[3.7,2.9],[3.2,2.6],[1.7,3.3],[3.4,2.6],[4.1,2.3],[3.0,2.9]])
#合并数据创造标签
X=np.concatenate((x1,x2))
y=np.concatenate((np.zeros(len(x1)),np.ones(len(x2))))4.2、先验概率
prior_probabilities=[np.sum(y==0)/len(y),np.sum(y==1)/len(y)]4.3、条件概率
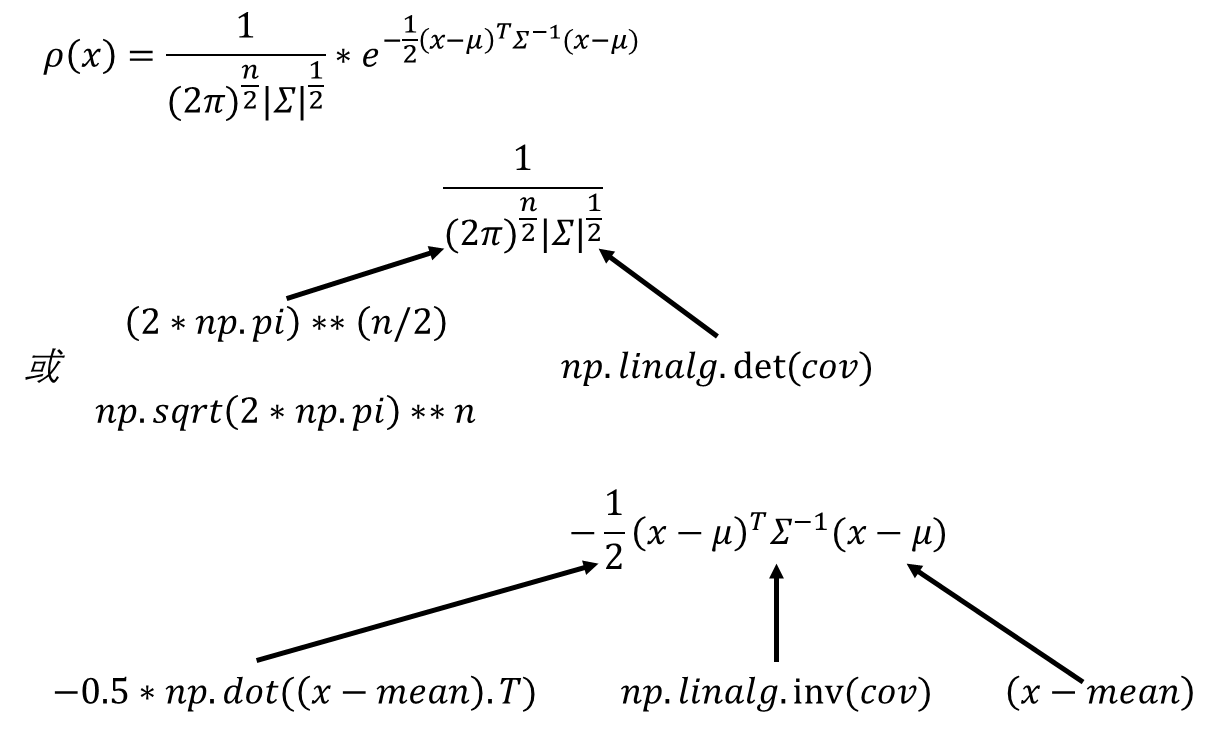
def pdf(x,mean,cov):n=len(mean)x1=1/((2*np.pi)**(n/2))*(np.sqrt(np.linalg.det(cov)))y1=-0.5*np.dot(np.dot((x-mean).T,np.linalg.inv(cov)),(x-mean))return x1*np.exp(y1)4.4、后验概率

posterior_probabilities=prior_probabilities[i]*likelinhood4.5、决策边界
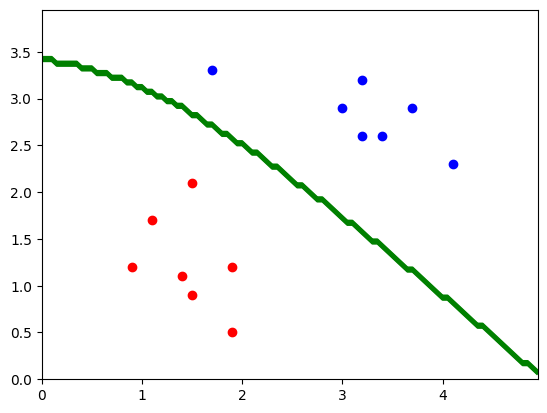
4.6、完整代码
import numpy as np
import matplotlib.pyplot as plt # 1. 散点输入
x1 = np.array([[1.9, 1.2], [1.5, 2.1], [1.9, 0.5], [1.5, 0.9], [0.9, 1.2], [1.1, 1.7], [1.4, 1.1]]) x2 = np.array([[3.2, 3.2], [3.7, 2.9], [3.2, 2.6], [1.7, 3.3], [3.4, 2.6], [4.1, 2.3], [3.0, 2.9]]) # 合并数据集、创造标签
X = np.concatenate((x1, x2)) # 将两个类别的数据点合并为一个数据集
y = np.concatenate((np.zeros(len(x1)), np.ones(len(x2)))) # 创建标签:类别1为0,类别2为1 # 2. 计算先验概率(每个类别的数据在数据集中的比例)
prior_probabilities = [np.sum(y == 0) / len(y), np.sum(y == 1) / len(y)]
print(prior_probabilities) # 输出每个类别的先验概率 # 3. 计算高斯分布的概率密度函数
# 求解每个类别的均值
class_means = [np.mean(X[y == 0], axis=0), np.mean(X[y == 1], axis=0)]
# print(class_means) # 输出每个类别的均值 # 求解每个类别的协方差矩阵
X_y_0 = X[y == 0].T # 类别0的数据点转置
X_y_1 = X[y == 1].T # 类别1的数据点转置
class_covs = [np.cov(X_y_0), np.cov(X_y_1)] # 计算每个类别的协方差矩阵 # 生成网格点,用于绘制决策边界
xx, yy = np.meshgrid(np.arange(0, 5, 0.05), np.arange(0, 4, 0.05))
# 预测网格点
grid_points = np.c_[xx.ravel(), yy.ravel()] # 将网格点展平并合并为二维点 def pdf(x, mean, cov): # 获取均值向量的长度,即特征的数量 n = len(mean) # 计算PDF的系数部分 coeff = 1 / ((2 * np.pi) ** (n / 2) * np.sqrt(np.linalg.det(cov))) # 计算归一化常数 # 计算PDF的指数部分 exponet = -0.5 * np.dot(np.dot((x - mean).T, np.linalg.inv(cov)), (x - mean)) # 计算指数部分 return coeff * np.exp(exponet) # 返回概率密度 grid_label = [] # 保存每个网格点的预测标签
# 每一组网格点进行预测
for point in grid_points: posterior_probabilities = [] # 存储后验概率 for i in range(2): # 使用高斯分布的概率密度函数求解条件概率 likelihood = pdf(point, class_means[i], class_covs[i]) # 计算似然 # 4. 得到后验概率,比较大小,获得分类 posterior_probabilities.append(prior_probabilities[i] * likelihood) # 计算后验概率 # 比较大小,获得分类 pre_class = np.argmax(posterior_probabilities) # 选择具有最大后验概率的类 grid_label.append(pre_class) # 保存预测标签 # 5. 显示决策边界
# 将预测的标签形状调整为与xx一致
grid_label = np.array(grid_label).reshape(xx.shape) # 重塑预测标签为与网格点一致的形状 # 绘制散点图
plt.scatter(x1[:, 0], x1[:, 1], c="blue", label="class 1") # 类别1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="red", label="class 2") # 类别2的散点图 contour = plt.contour(xx, yy, grid_label, levels=[0.5], colors="green") # 绘制决策边界 plt.legend() # 添加图例
plt.show() # 显示图表 五、多分类
import numpy as np
import matplotlib.pyplot as plt # 1. 散点输入
x1 = np.array([[1.9, 1.2], [1.5, 2.1], [1.9, 0.5], [1.5, 0.9], [0.9, 1.2], [1.1, 1.7], [1.4, 1.1]]) x2 = np.array([[3.2, 3.2], [3.7, 2.9], [3.2, 2.6], [1.7, 3.3], [3.4, 2.6], [4.1, 2.3], [3.0, 2.9]]) x3 = np.array([[3.3, 1.2], [3.8, 0.9], [3.3, 0.6], [2.8, 1.3], [3.5, 0.6], [4.2, 0.3], [3.1, 0.9]]) # 合并数据集、创造标签
X = np.concatenate((x1, x2, x3)) # 将三个类别的数据点合并为一个数据集
# 创建标签:类别1为0,类别2为1,类别3为2
y = np.concatenate((np.zeros(len(x1)), np.ones(len(x2)), 2 * np.ones(len(x3)))) # 2. 计算先验概率(每个类别的数据在数据集中的比例)
prior_probabilities = [np.sum(y == 0) / len(y), np.sum(y == 1) / len(y), np.sum(y == 2) / len(y)] # 3. 计算高斯分布的概率密度函数
# 求解每个类别的均值
class_mean = [np.mean(X[y == 0], axis=0), np.mean(X[y == 1], axis=0), np.mean(X[y == 2], axis=0)] # 求解每个类别的协方差矩阵
X_y_0 = X[y == 0].T # 类别0的数据点转置
X_y_1 = X[y == 1].T # 类别1的数据点转置
X_y_2 = X[y == 2].T # 类别2的数据点转置
class_covs = [np.cov(X_y_0), np.cov(X_y_1), np.cov(X_y_2)] # 计算每个类别的协方差矩阵 # 生成网格点,用于绘制决策边界
xx, yy = np.meshgrid(np.arange(0, 5, 0.05), np.arange(0, 4, 0.05))
# 预测网格点
grid_points = np.c_[xx.ravel(), yy.ravel()] # 将网格点展平并合并为二维点 def pdf(x, mean, cov): # 获取均值向量的长度,即特征的数量 n = len(mean) # 计算PDF的系数部分 coeff = 1 / ((2 * np.pi) ** (n / 2) * np.sqrt(np.linalg.det(cov))) # 计算归一化常数 # 计算PDF的指数部分 exponet = -0.5 * np.dot(np.dot((x - mean).T, np.linalg.inv(cov)), (x - mean)) # 计算指数部分 return coeff * np.exp(exponet) # 返回概率密度 grid_label = [] # 保存每个网格点的预测标签
# 每一组网格点进行预测
for point in grid_points: posterior_probabilities = [] # 存储后验概率 for i in range(3): # 遍历每个类别 # 使用高斯分布的概率密度函数求解条件概率 likelihood = pdf(point, class_mean[i], class_covs[i]) # 计算似然 # 4. 得到后验概率,比较大小,获得分类 posterior_probabilities.append(pr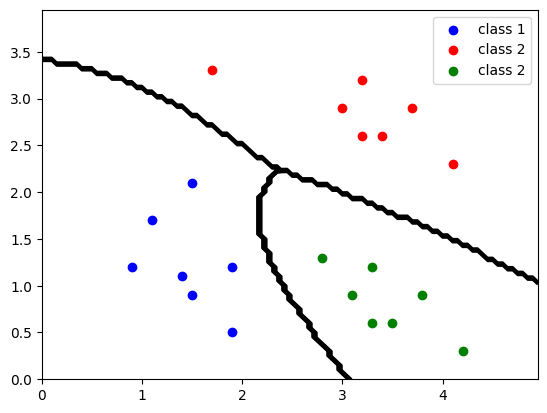
六、库函数
6.1、concatenate()
用于将多个数组连接在一起,通常在合并不同类别的数据时使用。
numpy.concatenate((a1, a2, ...), axis=0, out=None) | 方法 | 描述 |
|---|---|
| a1, a2, ... | 要连接的数组序列,可以是任意数量的数组。 |
| axis(可选) | 指定沿着哪个轴连接,默认值为 0。 |
| out(可选) | 与返回值相同形状的输出数组。 |
import numpy as np x1 = np.array([[1, 2], [3, 4]])
x2 = np.array([[5, 6], [7, 8]])
result = np.concatenate((x1, x2), axis=0)
# 输出:[[1 2]
# [3 4]
# [5 6]
# [7 8]] 6.2、cov()
用于计算每个特征的协方差矩阵,常用于概率分布分析和数据的分散程度。
numpy.cov(m, rowvar=True, bias=False, ddof=None, fweights=None, aweights=None) | 方法 | 描述 |
|---|---|
| m | 输入数据,可以是一个二维数组或矩阵。 |
| rowvar(可选) | 如果为 True(默认值),每一行代表一个变量,每一列代表一个观察结果。 |
| bias(可选) | 如果为 True,计算的是总体协方差矩阵;如果为 False,计算的是样本协方差矩阵。 |
| ddof(可选) | 用于设置自由度调整。 |
fweights,aweights(可选) | 用于加权相关分析。 |
import numpy as np data = np.array([[1, 2], [3, 4], [5, 6]])
cov_matrix = np.cov(data, rowvar=False)
# 输出:[[2. 2.]
# [2. 2.]] 6.3、meshgrid()
用于生成网格点,通常用于绘制二维图形,如决策边界。
numpy.meshgrid(*xi, indexing='xy', sparse=False) | 方法 | 描述 |
|---|---|
| *xi | 一维数组,表示网格点的坐标。 |
| indexing(可选) | 选择 'xy' 或 'ij' 来指定输出数组的排列顺序。 |
sparse(可选) | 如果为 True,则只返回稀疏网格。 |
import numpy as np x = np.arange(0, 5, 1)
y = np.arange(0, 3, 1)
xx, yy = np.meshgrid(x, y)
# xx: [[0, 1, 2, 3, 4],
# [0, 1, 2, 3, 4],
# [0, 1, 2, 3, 4]]
# yy: [[0, 0, 0, 0, 0],
# [1, 1, 1, 1, 1],
# [2, 2, 2, 2, 2]] 6.4、c_()
将网格点展平并合并为二维点
numpy.c_[*args] | 方法 | 描述 |
|---|---|
| *args | 可以是多个一维数组、列表或其他可以转换为数组的对象。 |
import numpy as np x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
result = np.c_[x, y]
# 输出:[[1 4] 6.5、np.linalg.det()
用于计算方阵的行列式,行列式可以提供矩阵的一些性质,例如,它可以用来判断矩阵是否可逆(如果行列式为零,则矩阵不可逆)。
numpy.linalg.det(a) | 方法 | 描述 |
|---|---|
| a | 要计算行列式的方阵(二维数组)。 |
import numpy as np # 定义一个方阵
matrix = np.array([[1, 2], [3, 4]]) determinant = np.linalg.det(matrix) # 计算行列式
print(determinant) # 输出:-2.0 6.6、np.linalg.inv()
用于计算方阵的逆。逆矩阵是线性代数中的重要概念,能够用于求解线性方程组和其他涉及矩阵的操作。
numpy.linalg.inv(a) | 方法 | 描述 |
|---|---|
| a | 要计算其逆的方阵(二维数组)。 |
import numpy as np # 定义一个方阵
matrix = np.array([[1, 2], [3, 4]]) inverse_matrix = np.linalg.inv(matrix) # 计算矩阵的逆
print(inverse_matrix)
# 输出:
# [[-2. 1. ]
# [ 1.5 -0.5]] 6.7、plt.contour()
用于绘制二元函数的等高线图,通常用于数据可视化,展示函数在空间中的分布情况和趋势。在决策边界的可视化中,也经常使用该函数来显示不同类的分界线。
matplotlib.pyplot.contour(X, Y, Z, levels=None, **kwargs) | 方法 | 描述 |
|---|---|
| x | 用于绘制等高线的 x 坐标数组。 |
| y | 用于绘制等高线的 y 坐标数组。 |
| z | 用于绘制等高线的对应的 z 值,它必须与 X 和 Y 相同形状的数组。 |
levels(可选) | 指定绘制的等高线级别,可以是一个标量(表示绘制一定数量的水平线)或一个数组(表示特定的高度)。 |
| **kwargs | 其他绘图属性,如颜色、线型等。 |
import numpy as np
import matplotlib.pyplot as plt # 创建网格数据
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2)) # 计算 z 值 plt.contour(X, Y, Z) # 绘制等高线
plt.title("Contour Plot")
plt.xlabel("X-axis")
plt.ylabel("Y-axis")
plt.colorbar() # 添加颜色条
plt.show() 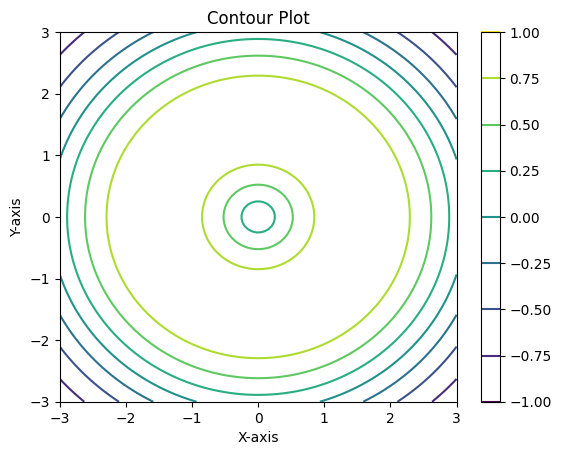











)


