图的应用之最短路径

引入

应用

算法思想

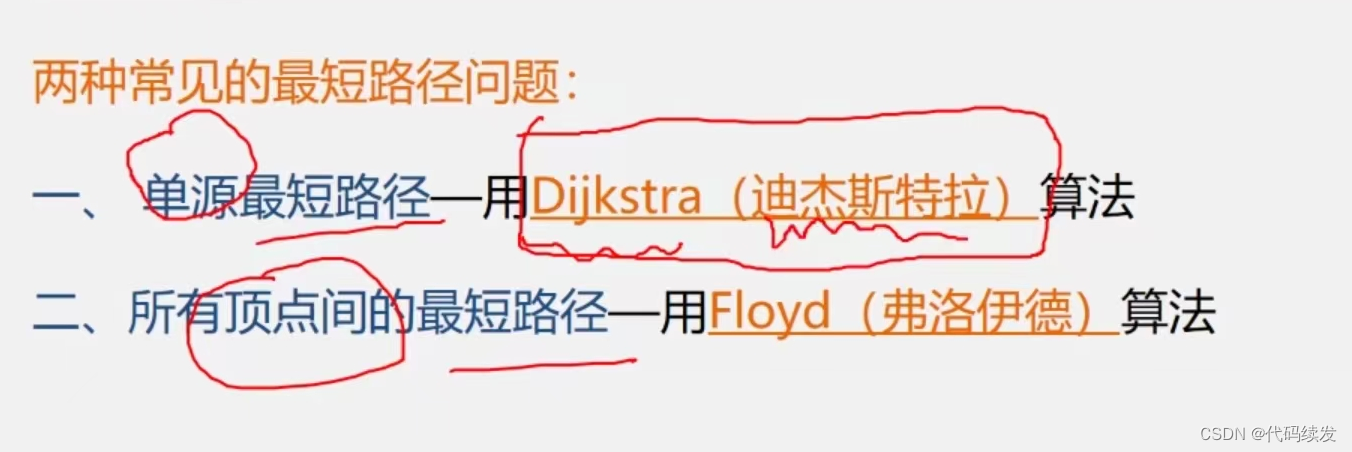
Dijistra算法

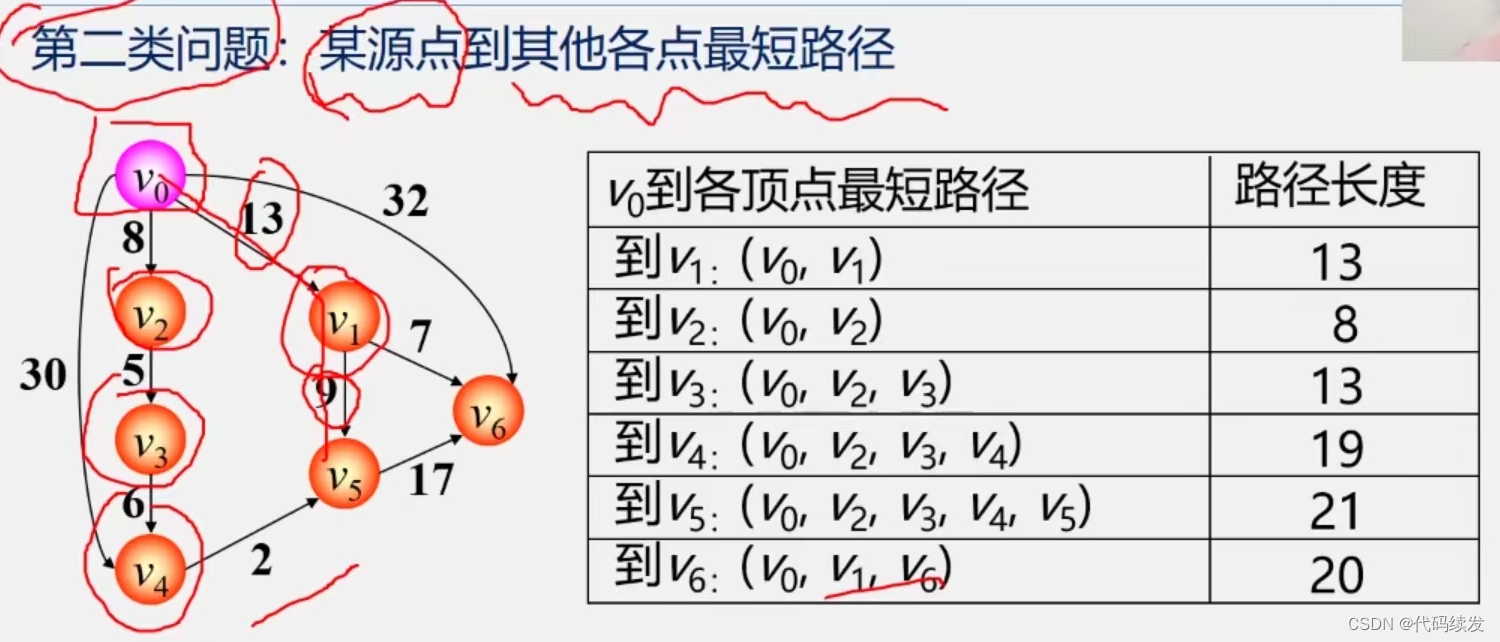
用于解决单个顶点间的最短路径问题

将顶点看成两部分：

最短路径顶点集合A与尚未确定最短路径顶点集合B。

先将顶点按最短路径由小到大依次加入到A中，选择由源点到A中最短的顶点，并记录距离与顶点，不断更新由源点到A中某个顶点的最短路径，直至全加入结束。

类似构造最小生成树的Prime算法，不断拓展顶点。

在负权图中，Dijkstra不能保证每次选出的顶点是真正最近顶点，由此也不能保证已定的最短路径不再改变，因此不适合求带负权值的最短路径。

Floyd算法

用于解决不同顶点间的最短路径问题。

两种算法的时间复杂度均为O(n*n*n)

先初始各顶点间的边，再依次加入各顶点更新边，拓展边。类似构造最小生成树中，先定顶点，再不断拓展边的Kruskal算法。

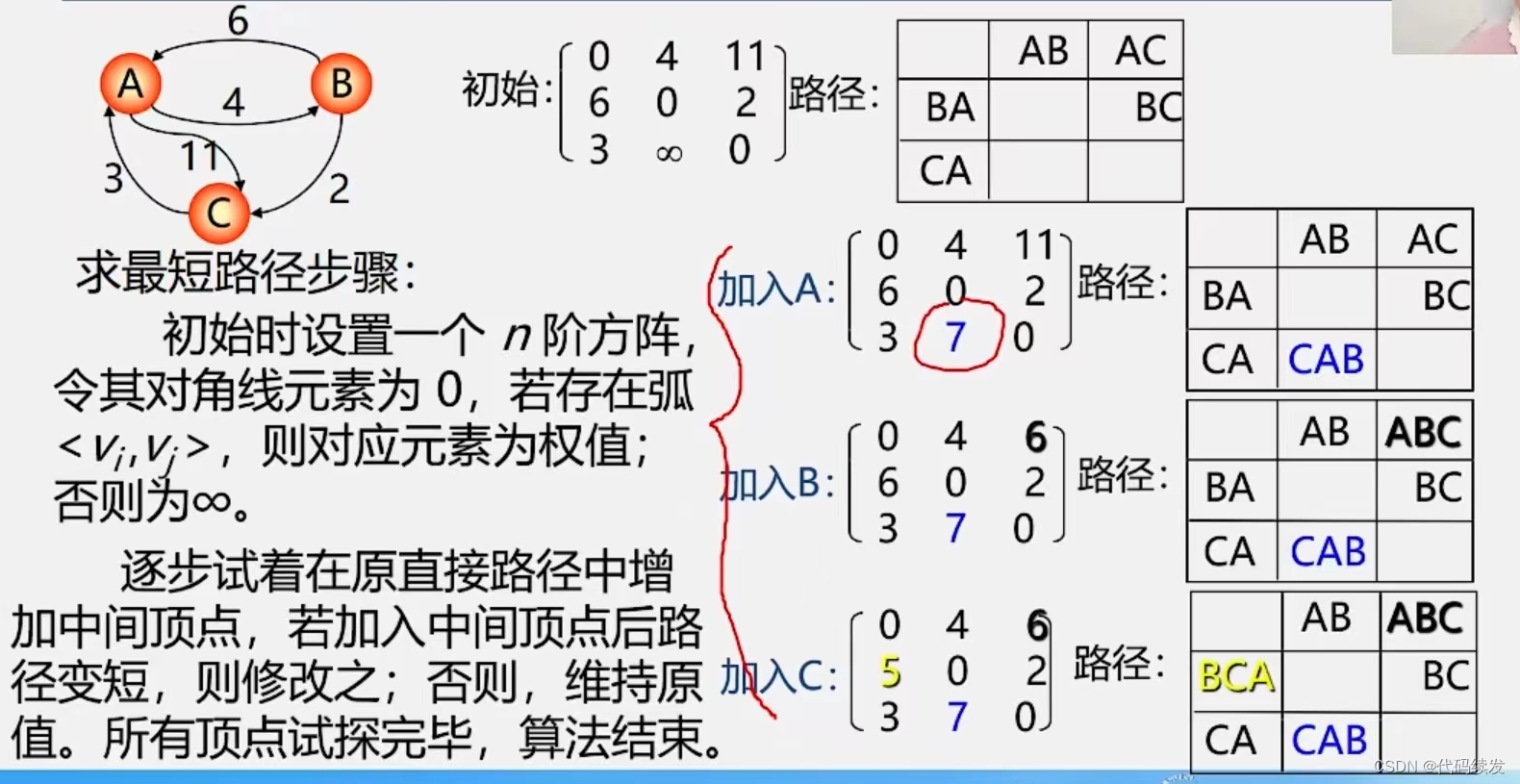
求最短路径允许有负边存在，但不允许包含负边组成的回路。

考点补充

1.最短路径是简单路径

最短路径是点与另一点间或点与其它多个点间权值最小的顶点集合，即组成最短路径的顶点集中各顶点均不相同。

而简单路径的定义为路径上的顶点均不相同。因此结论成立。

2.求解最短路径的其它算法

图的广度优先搜索算法-BFS：不断拓展顶点相关联的边中最小的边，直至访问完所有结点结束，实际就是由一个顶点出发，不断找与其相连的最小边的过程，即求最短路径的过程。

而求最小生成树算法(Prim与Kruskal算法)是保证整棵树的权值之和最小，而不一定保证源点到终点间的权值最小，即不一定具有最短路径的性质。

代码实现