十字链表存储有向图
橙色入度,绿色出度
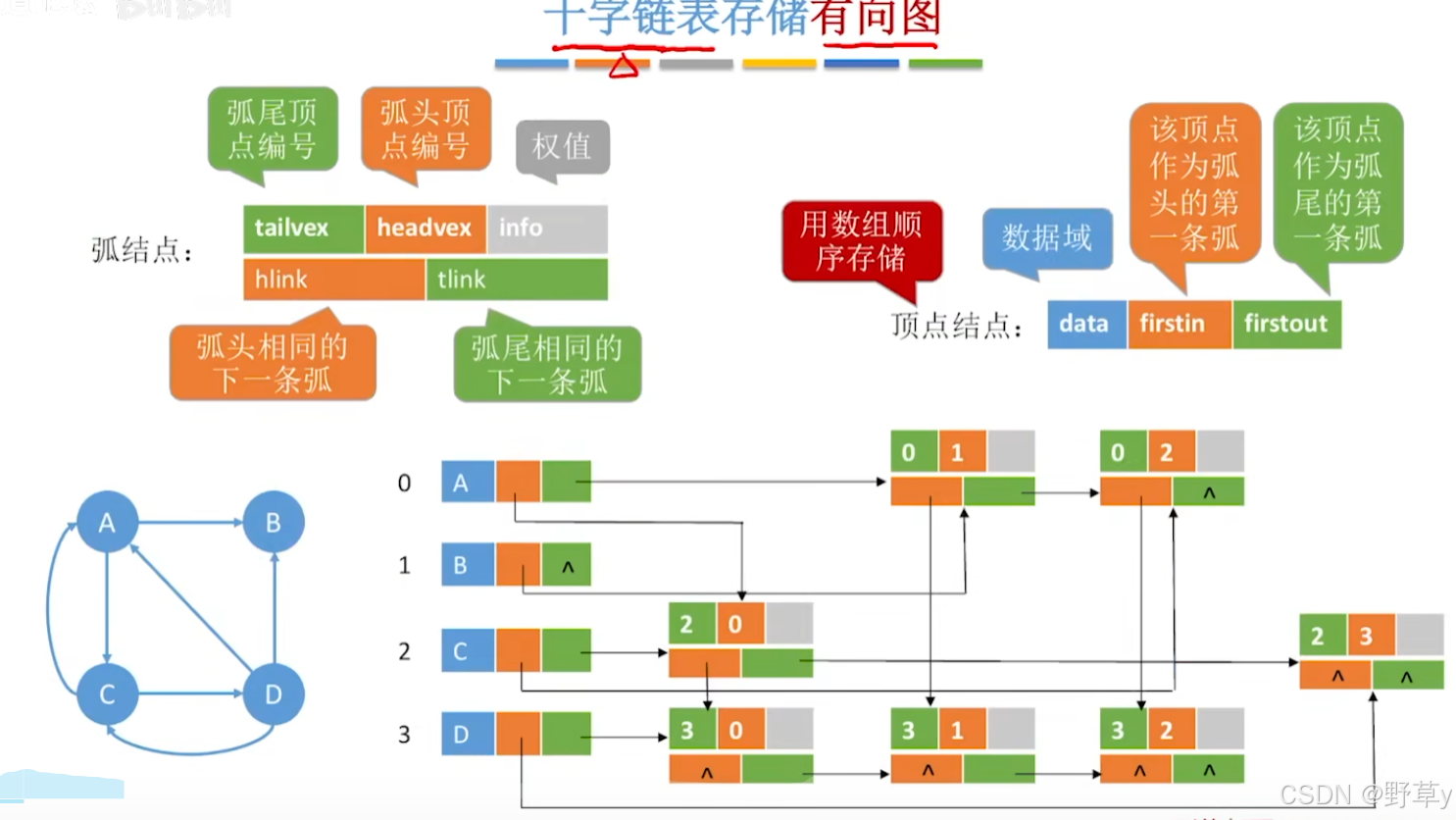
代码示例:
#include <stdio.h>
#include <stdlib.h>// 定义十字链表节点结构体
typedef struct OLNode {int row; // 行号int col; // 列号int value; // 节点值struct OLNode* right; // 指向右边节点的指针struct OLNode* down; // 指向下方节点的指针
} OLNode, * OLink;// 定义十字链表的头节点结构体
typedef struct {OLink* row_head; // 行表头指针数组OLink* col_head; // 列表头指针数组int m, n, len; // 矩阵的行数、列数和非零元素的个数
} CrossList;
// 创建十字链表
CrossList CreateCrossList(int m, int n) {CrossList M;M.m = m;M.n = n;M.len = 0;// 初始化行和列的头指针数组M.row_head = (OLink*)malloc((m + 1) * sizeof(OLink));M.col_head = (OLink*)malloc((n + 1) * sizeof(OLink));if (!M.row_head || !M.col_head) {exit(1); // 内存分配失败}for (int i = 1; i <= m; i++) {M.row_head[i] = NULL;}for (int j = 1; j <= n; j++) {M.col_head[j] = NULL;}return M;
}
// 向十字链表插入元素
void Insert(CrossList* M, int i, int j, int value) {if (i > M->m || j > M->n || value == 0) {return; // 插入位置不合法或值为0}// 创建新节点OLNode* newNode = (OLNode*)malloc(sizeof(OLNode));newNode->row = i;newNode->col = j;newNode->value = value;newNode->right = NULL;newNode->down = NULL;// 插入行if (M->row_head[i] == NULL) {M->row_head[i] = newNode;}else {OLNode* current = M->row_head[i];while (current->right && current->right->col < j) {current = current->right;}newNode->right = current->right;current->right = newNode;}// 插入列if (M->col_head[j] == NULL) {M->col_head[j] = newNode;}else {OLNode* current = M->col_head[j];while (current->down && current->down->row < i) {current = current->down;}newNode->down = current->down;current->down = newNode;}M->len++; // 更新非零元素个数
}
// 从十字链表删除元素
void Delete(CrossList* M, int i, int j) {if (i > M->m || j > M->n) {return; // 位置不合法}// 查找要删除的节点OLNode* p = M->row_head[i];while (p && p->col < j) {p = p->right;}if (p && p->col == j) {// 删除行中的节点if (p == M->row_head[i]) {M->row_head[i] = p->right;}else {OLNode* q = M->row_head[i];while (q->right != p) {q = q->right;}q->right = p->right;}// 删除列中的节点if (p == M->col_head[j]) {M->col_head[j] = p->down;}else {OLNode* q = M->col_head[j];while (q->down != p) {q = q->down;}q->down = p->down;}free(p); // 释放节点内存M->len--; // 更新非零元素个数}
}
// 在十字链表中查找元素
OLNode* Find(CrossList M, int i, int j) {if (i > M.m || j > M.n) {return NULL; // 位置不合法}OLNode* p = M.row_head[i];while (p && p->col < j) {p = p->right;}if (p && p->col == j) {return p; // 找到元素,返回节点指针}else {return NULL; // 未找到元素}
}
// 打印十字链表
void PrintCrossList(CrossList M) {printf("十字链表如下:\n");for (int i = 1; i <= M.m; i++) {OLNode* p = M.row_head[i];while (p) {printf("(%d, %d, %d) ", p->row, p->col, p->value);p = p->right;}printf("\n");}
}
// 释放十字链表
void FreeCrossList(CrossList* M) {for (int i = 1; i <= M->m; i++) {OLNode* p = M->row_head[i];while (p) {OLNode* q = p;p = p->right;free(q);}}free(M->row_head);free(M->col_head);
}
int main() {int m = 3, n = 4; // 定义一个3行4列的稀疏矩阵CrossList M = CreateCrossList(m, n); // 创建十字链表// 插入元素Insert(&M, 1, 2, 12);Insert(&M, 1, 4, 9);Insert(&M, 3, 1, -3);Insert(&M, 3, 3, 14);// 打印十字链表PrintCrossList(M);// 删除元素Delete(&M, 1, 2);// 再次打印十字链表printf("删除元素后的十字链表:\n");PrintCrossList(M);// 释放十字链表FreeCrossList(&M);return 0;
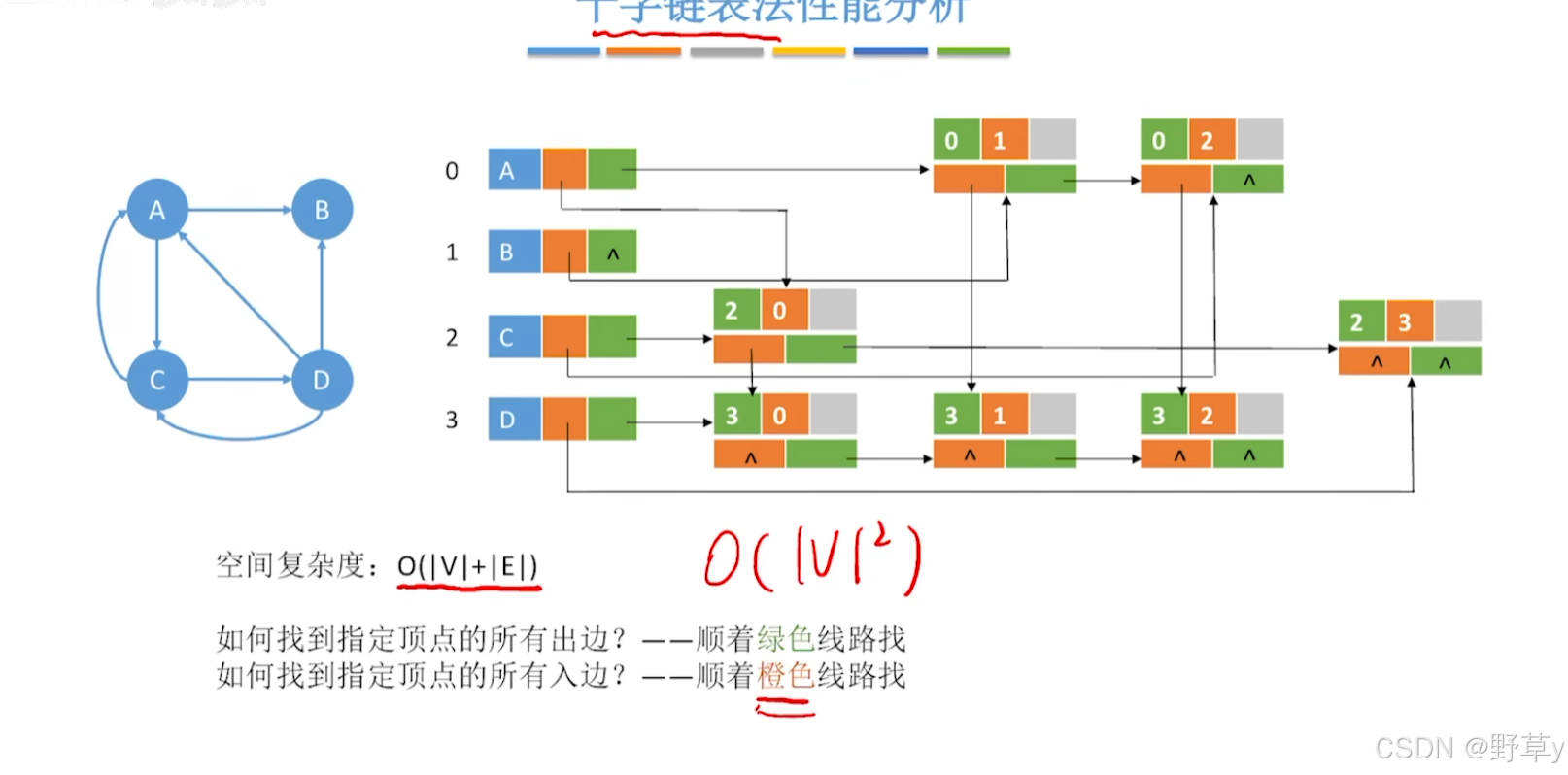
}十字链表法性能分析
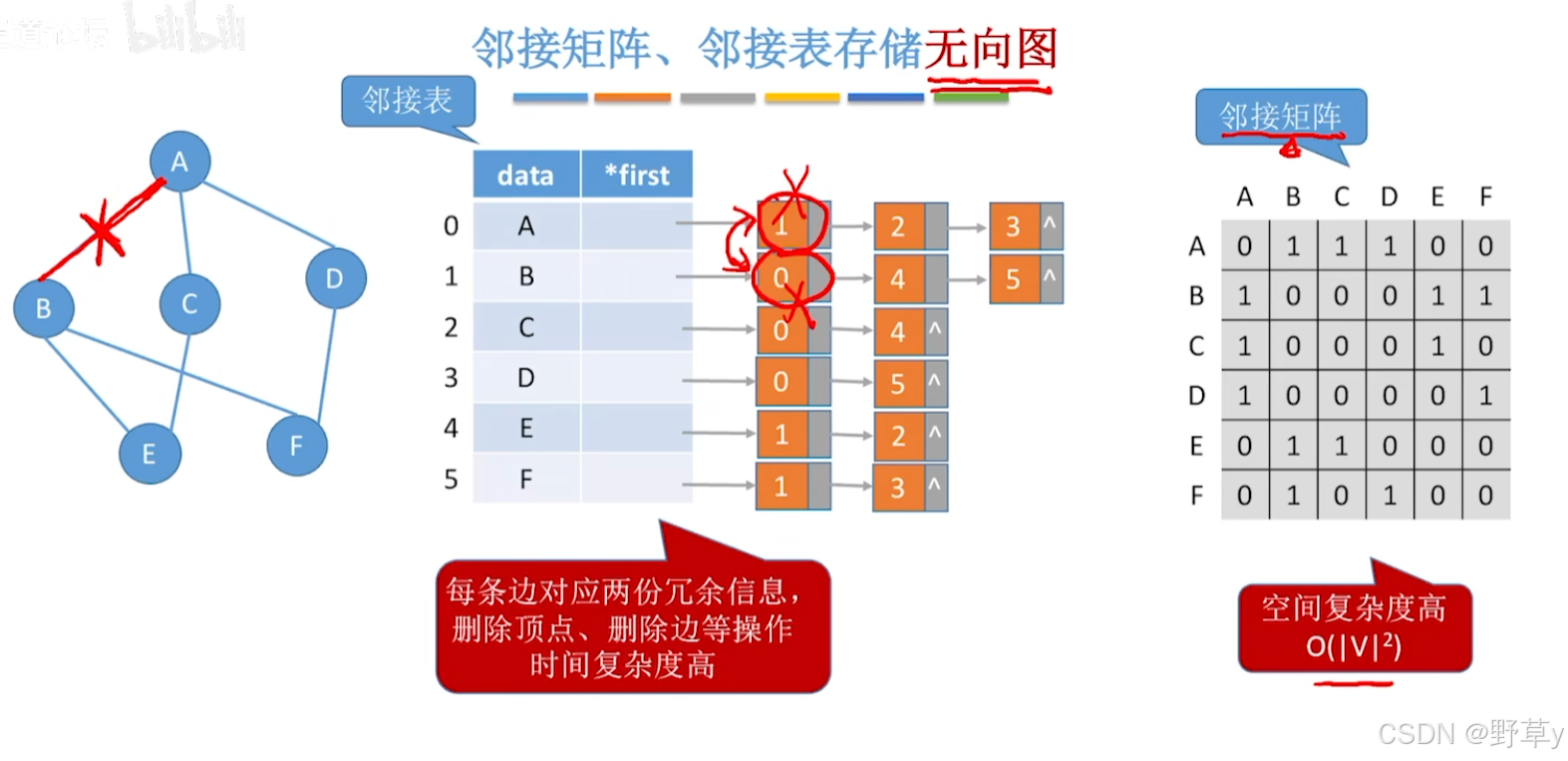
领接矩阵、邻接表存储无向图的缺点
邻接多重表存储无向图
优点:
每一条边只对应一个边结点,没有冗余数据,删除结点或者删除边的时候会方便很多
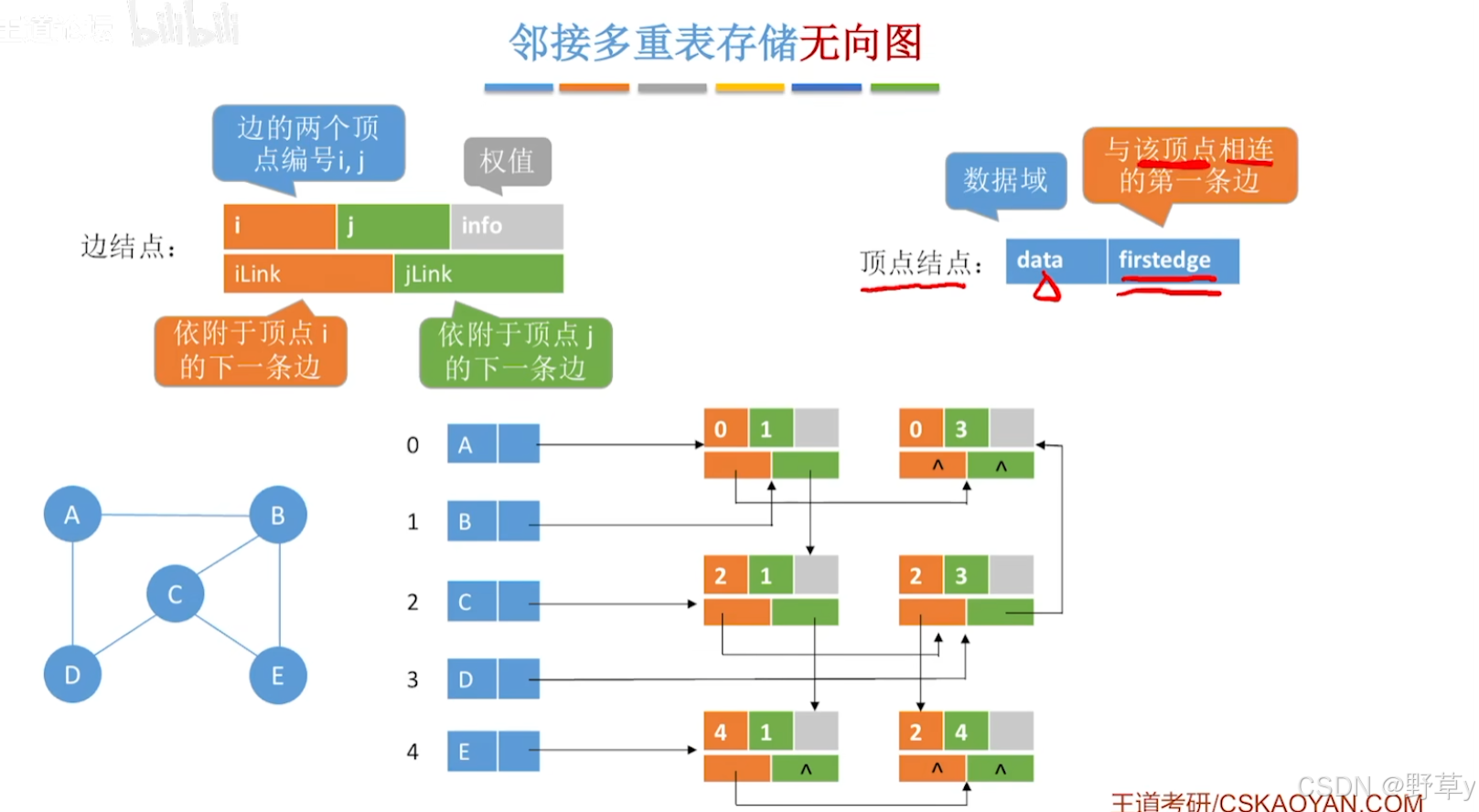
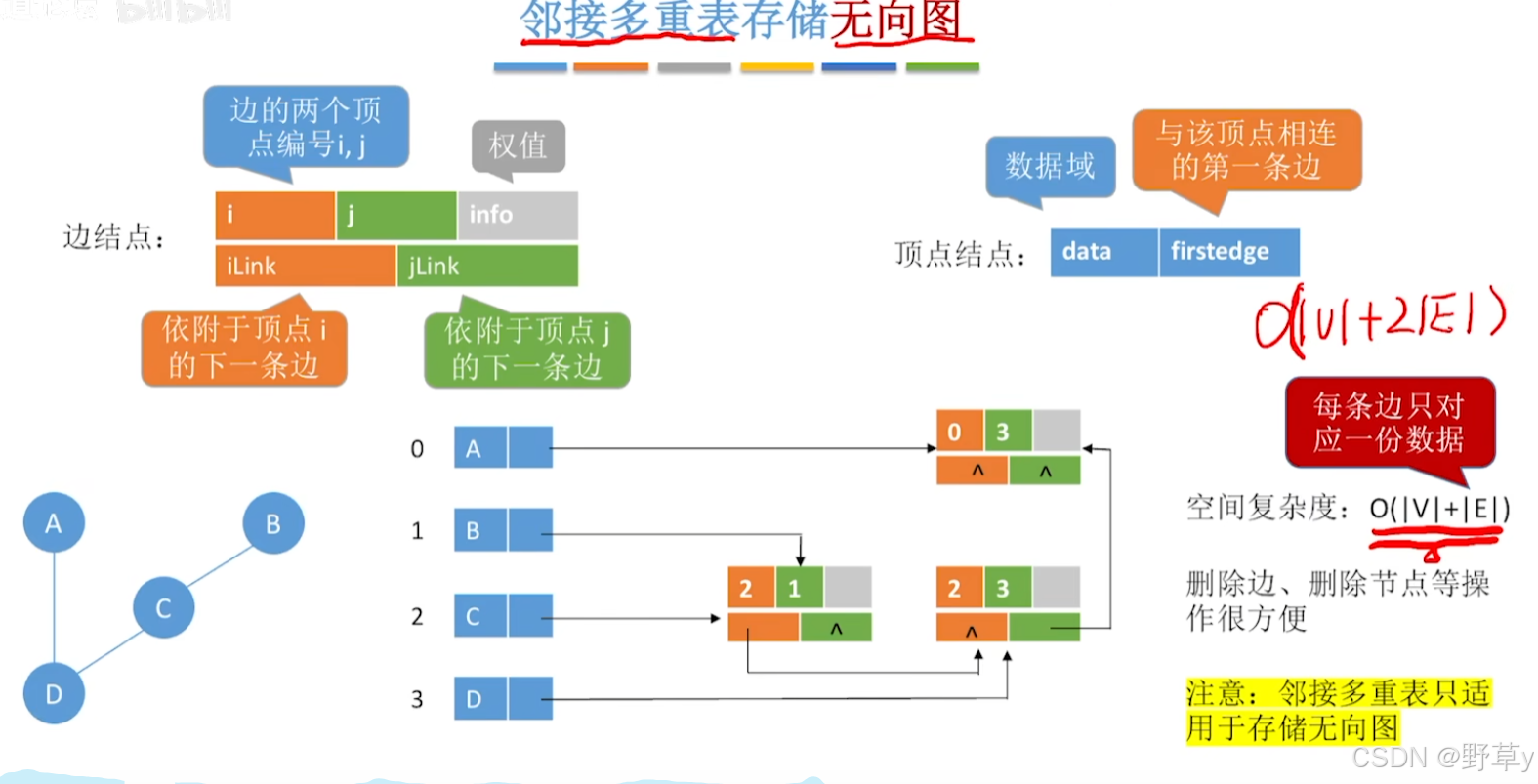
代码示例:
#include <stdio.h>
#include <stdlib.h>// 定义邻接多重表的边节点结构体
typedef struct EdgeNode {int ivex; // 边的起点int jvex; // 边的终点struct EdgeNode* ilink; // 指向起点相同的下一条边struct EdgeNode* jlink; // 指向终点相同的下一条边int mark; // 标记边是否被访问过
} EdgeNode;// 定义邻接多重表的顶点节点结构体
typedef struct VertexNode {int data; // 顶点数据EdgeNode* firstedge; // 指向第一条依附于该顶点的边
} VertexNode;// 定义邻接多重表结构体
typedef struct {VertexNode* vertices; // 顶点表int vexnum, edgenum; // 顶点数和边数
}AMLGraph;
// 创建邻接多重表
AMLGraph CreateAMLGraph(int vexnum, int edgenum) {AMLGraph graph;graph.vexnum = vexnum;graph.edgenum = edgenum;// 初始化顶点表graph.vertices = (VertexNode*)malloc(vexnum * sizeof(VertexNode));if (!graph.vertices) {exit(1); // 内存分配失败}for (int i = 0; i < vexnum; i++) {graph.vertices[i].data = i;graph.vertices[i].firstedge = NULL;}return graph;
}
// 插入边
void InsertEdge(AMLGraph* graph, int ivex, int jvex) {// 创建边节点EdgeNode* newEdge = (EdgeNode*)malloc(sizeof(EdgeNode));newEdge->ivex = ivex;newEdge->jvex = jvex;newEdge->ilink = graph->vertices[ivex].firstedge;newEdge->jlink = graph->vertices[jvex].firstedge;newEdge->mark = 0;// 插入到顶点ivex的边表graph->vertices[ivex].firstedge = newEdge;// 插入到顶点jvex的边表graph->vertices[jvex].firstedge = newEdge;
}
// 删除边
void DeleteEdge(AMLGraph* graph, int ivex, int jvex) {EdgeNode* p = graph->vertices[ivex].firstedge;EdgeNode* pre = NULL;while (p && (p->ivex != ivex || p->jvex != jvex)) {pre = p;if (p->ivex == ivex) {p = p->ilink;}else {p = p->jlink;}}if (p) {if (pre) {if (p->ivex == ivex) {pre->ilink = p->ilink;}else {pre->jlink = p->jlink;}}else {if (p->ivex == ivex) {graph->vertices[ivex].firstedge = p->ilink;}else {graph->vertices[jvex].firstedge = p->jlink;}}free(p);}
}
// 查找顶点
VertexNode* FindVertex(AMLGraph graph, int data) {for (int i = 0; i < graph.vexnum; i++) {if (graph.vertices[i].data == data) {return &graph.vertices[i];}}return NULL;
}
// 打印邻接多重表
void PrintAMLGraph(AMLGraph graph) {printf("邻接多重表如下:\n");for (int i = 0; i < graph.vexnum; i++) {EdgeNode* p = graph.vertices[i].firstedge;while (p) {int ivex = p->ivex;printf("(%d, %d) ", ivex, jvex);// 根据当前顶点,决定移动到ilink还是jlinkif (ivex == i) {p = p->ilink;}else {p = p->jlink;}}printf("\n");}
}
// 释放邻接多重表
void FreeAMLGraph(AMLGraph* graph) {for (int i = 0; i < graph->vexnum; i++) {EdgeNode* p = graph->vertices[i].firstedge;while (p) {EdgeNode* q = p;p = p->ilink;free(q);}}free(graph->vertices);
}
int main() {int vexnum = 4; // 定义顶点数为4int edgenum = 5; // 定义边数为5AMLGraph graph = CreateAMLGraph(vexnum, edgenum); // 创建邻接多重表// 插入边InsertEdge(&graph, 0, 1);InsertEdge(&graph, 0, 2);InsertEdge(&graph, 1, 2);InsertEdge(&graph, 1, 3);InsertEdge(&graph, 2, 3);// 打印邻接多重表PrintAMLGraph(graph);// 删除边DeleteEdge(&graph, 1, 2);// 再次打印邻接多重表printf("删除边后的邻接多重表:\n");PrintAMLGraph(graph);// 释放邻接多重表FreeAMLGraph(&graph);return 0;
}
总结:
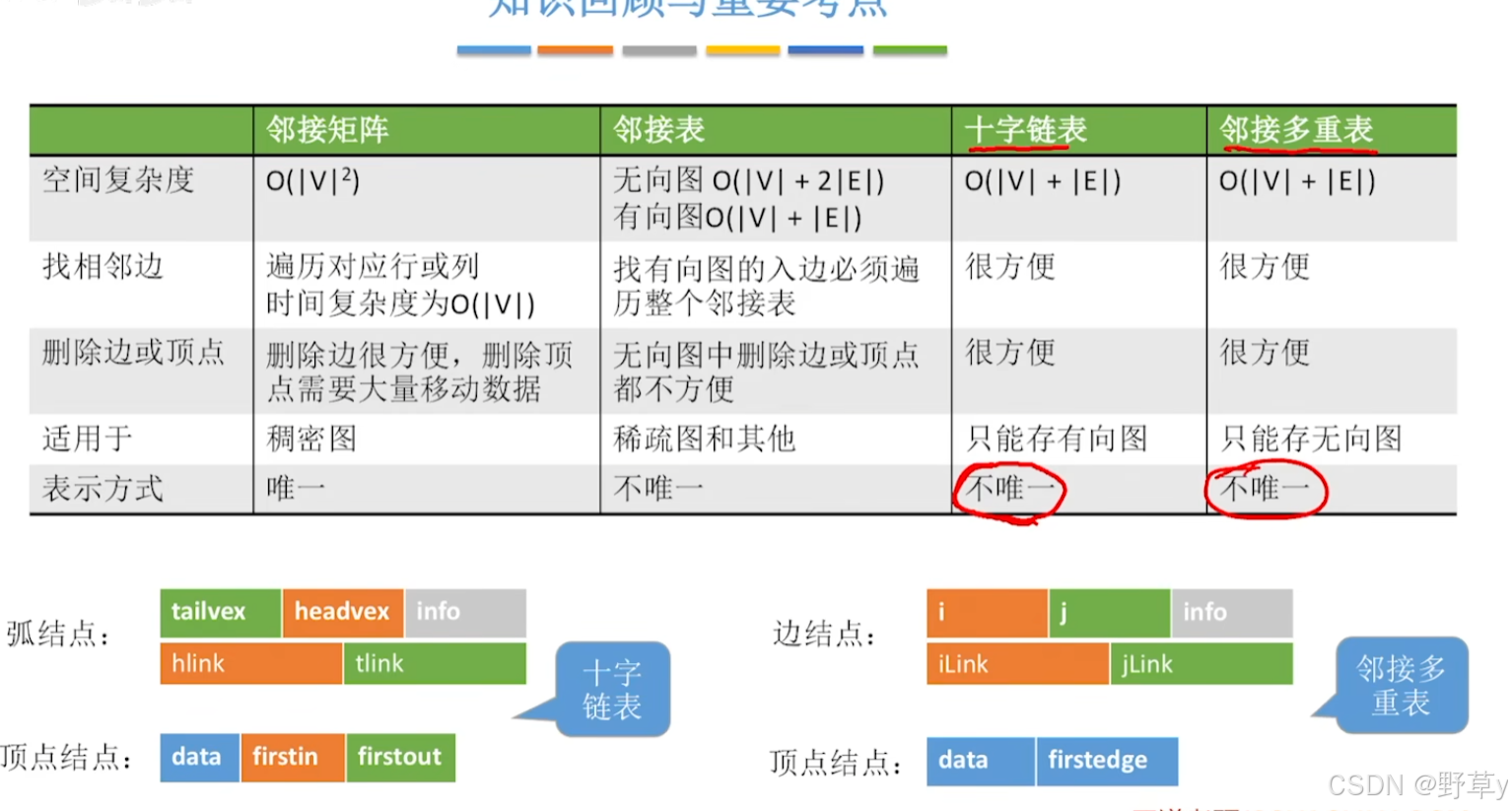











——十字链表法和多重领接表)


