中信建设公司董事长_四大软件外包公司_福州百度推广开户_域名比价网

麻雀搜索算法（Sparrow Search Algorithm，SSA）是一种新型的群智能优化算法，以下是详细介绍：

麻雀搜索算法-SSA-（可用于路径规划/自动化建筑结构设计/机械零件设计）

一、算法背景

起源
- 麻雀搜索算法是受到麻雀觅食行为和反捕食行为的启发而提出的。麻雀在觅食过程中，既存在寻找食物源的探索行为，又存在在食物源周围进行开采食物的利用行为。同时，麻雀群体还会对捕食者的威胁做出反应，这种行为特点被用于设计优化算法。
发展目的
- 它主要用于解决复杂的优化问题，如函数优化、工程设计优化、机器学习中的参数优化等领域。在实际应用中，很多问题可以抽象为寻找最优解的数学模型，而麻雀搜索算法能够有效地在解空间中搜索到较优的解。

二、算法原理

麻雀种群的划分
- 在麻雀搜索算法中，麻雀种群分为发现者（Producer）和加入者（Scrounger）。发现者通常占种群的一部分比例（例如 10% - 20%），它们在搜索空间中积极探索，寻找食物丰富的区域，引导整个种群的搜索方向。其位置更新公式如下：
  
  其中，是第代第只麻雀在第维的位置，是一个常数（通常在之间），是最大迭代次数。
- 加入者则会根据发现者的位置来更新自己的位置，以获取食物。它们主要在发现者周围进行搜索，其位置更新公式与发现者位置和自身位置等因素有关。
预警机制
- 麻雀群体还具有预警机制。当有捕食者出现（在算法中可以理解为算法陷入局部最优等不良情况）时，一部分麻雀（警戒者）会放弃当前的食物源，飞到安全的区域。这一过程通过相应的位置更新规则来实现，从而使算法能够跳出局部最优，增强全局搜索能力。
- 例如，当麻雀察觉到危险时，其位置更新公式为：
  
  其中，是服从正态分布的随机数，是一个（为维度）的矩阵，其元素全部为 1。这使得麻雀能够随机地改变位置，避免被捕食者捕获，在算法中就是避免陷入局部最优解。
算法的迭代过程
- 在每次迭代中，首先更新发现者的位置，然后更新加入者的位置，最后根据预警机制更新警戒者的位置。通过不断地迭代这个过程，使麻雀种群不断地在搜索空间中寻找最优解，直到满足停止条件（如达到最大迭代次数或找到满足精度要求的解）。

三、算法步骤

初始化
- 确定麻雀种群的大小、最大迭代次数、问题的维度等参数。然后在搜索空间中随机初始化麻雀种群的位置（的矩阵）。
计算适应度值
- 根据目标函数计算每个麻雀的适应度值，适应度值用于衡量麻雀位置（即解）的优劣。
迭代更新
- 按照发现者 - 加入者 - 警戒者的顺序更新麻雀的位置。
- 对于发现者，根据上述发现者位置更新公式更新其位置，并计算更新后的适应度值。
- 对于加入者，根据与发现者的关系更新位置并计算适应度。
- 根据预警机制更新警戒者的位置并计算适应度。
判断终止条件
- 如果迭代次数达到或者满足其他终止条件（如最优适应度值在多次迭代中不再变化），则输出最优解（即具有最优适应度值的麻雀位置）；否则，返回步骤 3 继续迭代。

四、应用领域

工程优化
- 在机械设计中，可用于优化机械结构的参数，如在设计汽车悬挂系统时，通过 SSA 优化悬挂参数，以提高汽车的舒适性和稳定性。在电路设计中，优化电路元件的参数，提高电路性能，如优化滤波器的参数，降低信号失真。
机器学习
- 用于神经网络的参数优化，如在训练深度学习模型时，SSA 可以优化神经网络的权重和偏置，加快训练速度并提高模型的精度。在支持向量机（SVM）中，优化核函数参数等，提高分类器的性能。
资源分配
- 在云计算环境中，优化虚拟机的资源分配，如 CPU、内存等资源的分配，提高云计算系统的整体性能和资源利用率。在通信网络中，优化频谱资源分配，提高频谱效率。

路径规划

机器人路径规划：在机器人的任务执行过程中，需要在复杂环境中找到从起始点到目标点的最佳路径。SSA 可以将机器人的路径表示为一系列的节点或坐标，通过模拟麻雀的觅食和反捕食行为，不断优化路径，使机器人能够避开障碍物，以最短的路径、最少的时间或最小的能量消耗到达目标点。例如在物流仓库中，利用 SSA 可以为移动机器人规划出高效的货物搬运路径，提高物流运输效率。
无人机路径规划：对于无人机在执行侦察、巡检等任务时，也面临着在复杂空域环境中规划安全、高效路径的问题。SSA 可以考虑无人机的飞行性能限制、空域限制、目标位置等因素，优化无人机的飞行路径，确保无人机能够完成任务并安全返回。比如在电力巡检中，使用 SSA 规划无人机的巡检路径，使其能够全面、高效地检查电力线路。

自动化建筑结构设计

整体布局优化：在建筑结构设计的初期，需要对建筑的整体布局进行规划，包括房间的分布、楼梯和电梯的位置、通道的设置等。SSA 可以根据建筑的功能需求、使用面积、采光通风等要求，对建筑的平面布局进行优化，找到最优的布局方案，提高建筑的空间利用率和使用舒适度。
结构参数设计：对于建筑的结构构件，如梁、柱、板等，SSA 可以优化其尺寸、形状和材料等参数。以框架结构为例，SSA 可以根据建筑的荷载要求、抗震等级等条件，调整梁和柱的截面尺寸、混凝土强度等级等参数，在保证结构安全的前提下，降低建筑成本和材料用量。

机械零件设计

零件形状优化：在机械零件的设计中，零件的形状对其性能和功能有着重要影响。SSA 可以根据零件的工作条件和性能要求，如强度、刚度、耐磨性等，对零件的形状进行优化。例如在设计汽车发动机的活塞时，利用 SSA 可以优化活塞的外形轮廓，提高其在气缸内的运动效率和密封性。
多参数协同设计：机械零件通常涉及多个参数的设计，如齿轮的模数、齿数、齿宽等参数。SSA 可以同时对这些参数进行优化，通过搜索最优的参数组合，使机械零件达到最佳的性能匹配。比如在设计多级齿轮传动系统时，使用 SSA 可以优化各级齿轮的参数，提高传动系统的传动效率和承载能力。

具体代码与实验结果

%% 
clear all %#ok<CLALL>
close all
clcN=50; % Number of search agentsFunction_name='F10'; % Name of the test function, range from F1-F23
iter=1000; % Maximum number of iteration times% Load details of the selected benchmark function
[lb,ub,dim,fobj]=CEC2005(Function_name);%% SSA
[fMin , bestX,SSA_Convergence_curve ] =SSA(N,iter,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by SSA  for ' [num2str(Function_name)],'  is : ', num2str(fMin)]);
fprintf ('Best solution obtained by SSA: %s\n', num2str(bestX,'%e  '));%% GWO
[Best_score,Best_pos,PSO_curve]=PSO(N,iter,lb,ub,dim,fobj);  % Calculating the solution of the given problem using PSO
display(['The best optimal value of the objective funciton found by PSO  for ', [num2str(Function_name)],'  is : ', num2str(Best_score)]);
fprintf ('Best solution obtained by PSO: %s\n', num2str(Best_pos,'%e  '));
%% gwo
[Alpha_score,Alpha_pos,GWO_Convergence_curve]=GWO(N,iter,lb,ub,dim,fobj);  % Calculating the solution of the given problem using gwo
display(['The best optimal value of the objective funciton found by GWO  for ', [num2str(Function_name)],'  is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by GWO: %s\n', num2str(Alpha_pos,'%e  '));%Draw objective space%% Figure
figure1 = figure('Color',[1 1 1]);
G1=subplot(1,2,1,'Parent',figure1);
func_plot(Function_name)
title(Function_name)
xlabel('x')
ylabel('y')
zlabel('z')
subplot(1,2,2)
G2=subplot(1,2,2,'Parent',figure1);
CNT=35;
k=round(linspace(1,iter,CNT)); %随机选CNT个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:iter;
semilogy(iter(k),PSO_curve(k),'b-^','linewidth',1);
hold on
semilogy(iter(k),GWO_Convergence_curve(k),'m-*','linewidth',1);
hold on
semilogy(iter(k),SSA_Convergence_curve(k),'g->','linewidth',1);
grid on;
title('收敛曲线')
xlabel('迭代次数');
ylabel('适应度值');
box on
legend('PSO','GWO','SSA')
set (gcf,'position', [300,300,800,320])

最优解比较
- SSA：通过调用 SSA 函数，得到了目标函数的最小最优值 fMin 和最佳位置 bestX。从 display 和 fprintf 输出的信息中，我们可以观察到 SSA 找到的最优值和最佳解。
- PSO：调用 PSO 函数得到 Best_score 和 Best_pos，代表 PSO 找到的最优值和最佳位置。
- GWO：调用 GWO 函数得到 Alpha_score 和 Alpha_pos，表示 GWO 找到的最优值和最佳位置。
比较这三种算法的最优值，我们可以直观地看出哪种算法在寻找 F10 函数的全局最优解方面表现更优。如果 fMin 的值最小，说明在本次实验中 SSA 可能找到了更好的解；如果 Best_score 最小，则 PSO 表现更优；如果 Alpha_score 最小，那么 GWO 可能是最优的。但需要注意的是，这仅仅是一次实验的结果，不同的测试函数和实验设置可能会导致不同的结果。

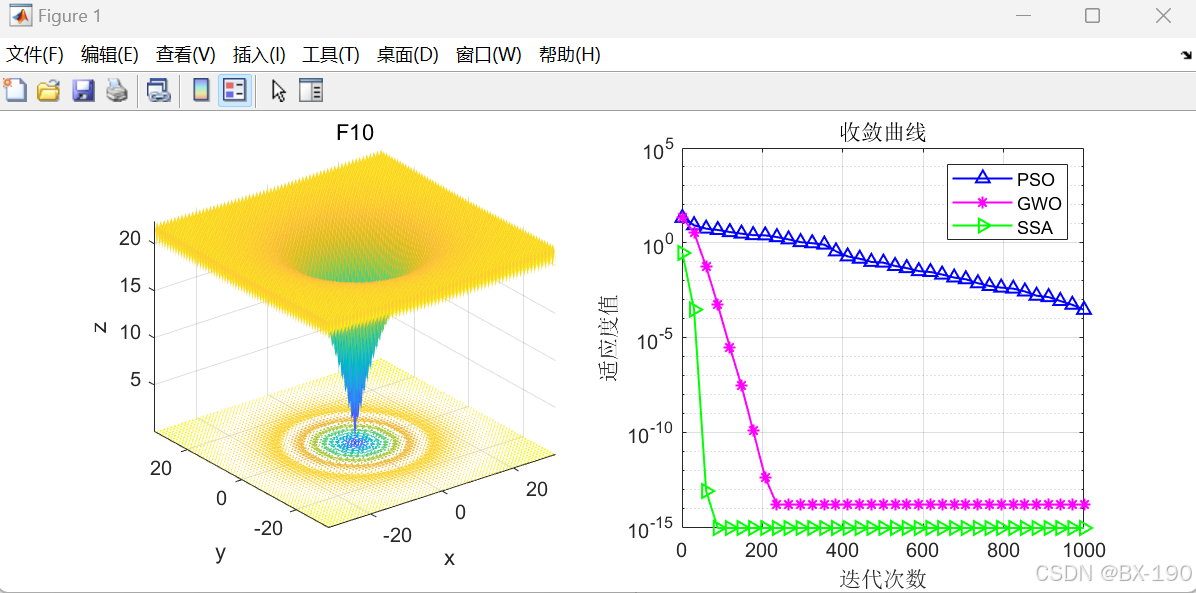
收敛曲线分析
- 在绘制的收敛曲线图中，使用半对数坐标绘制了三种算法的收敛曲线，横坐标是迭代次数（通过 iter(k) 选取了 CNT 个点），纵坐标是适应度值。
- PSO 收敛曲线（蓝色三角形）：观察 PSO_curve 的收敛情况，我们可以看到其下降趋势。如果曲线下降迅速且稳定，说明 PSO 在搜索过程中能够较快地找到较好的解，并且在后续迭代中不断优化。如果曲线在某个迭代次数后趋于平缓，可能意味着算法陷入了局部最优，难以进一步改进。
- GWO 收敛曲线（洋红色星号）：GWO_Convergence_curve 的走势反映了 GWO 的性能。与 PSO 曲线类似，快速下降的曲线表示算法在前期有较好的搜索能力，而后期曲线的平滑度则表示是否陷入局部最优或能否持续优化。
- SSA 收敛曲线（绿色右箭头）：SSA_Convergence_curve 展现了 SSA 的收敛特性。如果该曲线在早期阶段就能够达到较低的适应度值，并且持续下降到最低，可能说明 SSA 在探索和利用解空间方面具有优势。
通过对比三条曲线，我们可以得出以下几点：
- 收敛速度：观察曲线在前期下降的陡峭程度，越陡峭说明收敛速度越快。例如，如果 SSA 的曲线在开始阶段就迅速下降，说明它在早期搜索阶段比 PSO 和 GWO 更快地找到了较优解。
- 避免局部最优能力：如果一条曲线在迭代过程中出现停滞不前或缓慢下降的情况，而其他曲线继续下降，说明该算法可能更容易陷入局部最优。例如，若 GWO 曲线在某个迭代次数后基本保持不变，而 SSA 和 PSO 曲线仍在下降，那么 GWO 在本次实验中可能更易陷入局部最优。
- 最终性能：最终收敛到的适应度值是衡量算法性能的重要指标。比较三种曲线在迭代次数达到 1000 时的纵坐标值，越低说明最终性能越好。
算法稳定性评估
- 为了评估算法的稳定性，我们可以多次运行上述实验，观察在相同的测试函数和实验设置下，三种算法每次找到的最优值和收敛曲线的波动情况。
- 对于 SSA，如果多次运行得到的 fMin 波动较小，说明 SSA 对 F10 函数的优化性能较为稳定；如果 fMin 波动大，说明 SSA 受初始条件或随机因素的影响较大。
- 同理，对于 PSO 和 GWO，多次实验得到的 Best_score 和 Alpha_score 的波动情况反映了它们的稳定性。

三、总结

通过本次实验，我们对 SSA、PSO 和 GWO 三种优化算法在 F10 测试函数上进行了性能比较。从最优解的结果和收敛曲线可以看出，在特定的实验条件下（搜索代理数量为 50，最大迭代次数为 1000），三种算法表现出不同的特性：

SSA：可能在某些情况下表现出较好的探索和利用能力，其收敛曲线的形状可以反映它在搜索过程中的性能，最终找到的最优值可能是三种算法中最优的，但需要多次实验验证其稳定性。
PSO：在实验中其收敛速度和最终性能需要根据具体的收敛曲线进行判断，如果曲线前期下降快，可能是一个优点，但最终收敛的适应度值可能不是最好的，且存在陷入局部最优的可能性。
GWO：与其他两种算法类似，其性能取决于收敛曲线和最终的最优值，曲线的走势可以反映它在迭代过程中的表现，最终结果也可能因不同的测试函数而不同。

在实际应用中，我们可以根据不同的优化问题和性能要求，选择最适合的算法。例如，对于需要快速收敛的问题，可以选择在前期收敛速度快的算法；对于需要避免局部最优的问题，可以根据收敛曲线观察算法的抗局部最优能力。此外，为了更准确地评估算法性能，建议增加实验次数，改变搜索代理数量和迭代次数等参数，对不同测试函数进行测试，以全面了解三种算法的优缺点。

需要注意的是，实验结果受到测试函数的特性、参数设置以及算法本身的随机性的影响，因此上述分析仅为本次实验的初步结论，还需要进一步的实验和分析来深入比较这三种算法在不同场景下的性能。

麻雀搜索算法-SSA-（可用于路径规划/自动化建筑结构设计/机械零件设计）