leetcode-189. 旋转数组 原地递归算法（非官方的三种方法）

Problem: 189. 轮转数组

思路

首先，很明显，题目要求的操作等同于将数组的后k%n个元素移动到前面来。
然后我们思考原地操作的方法：
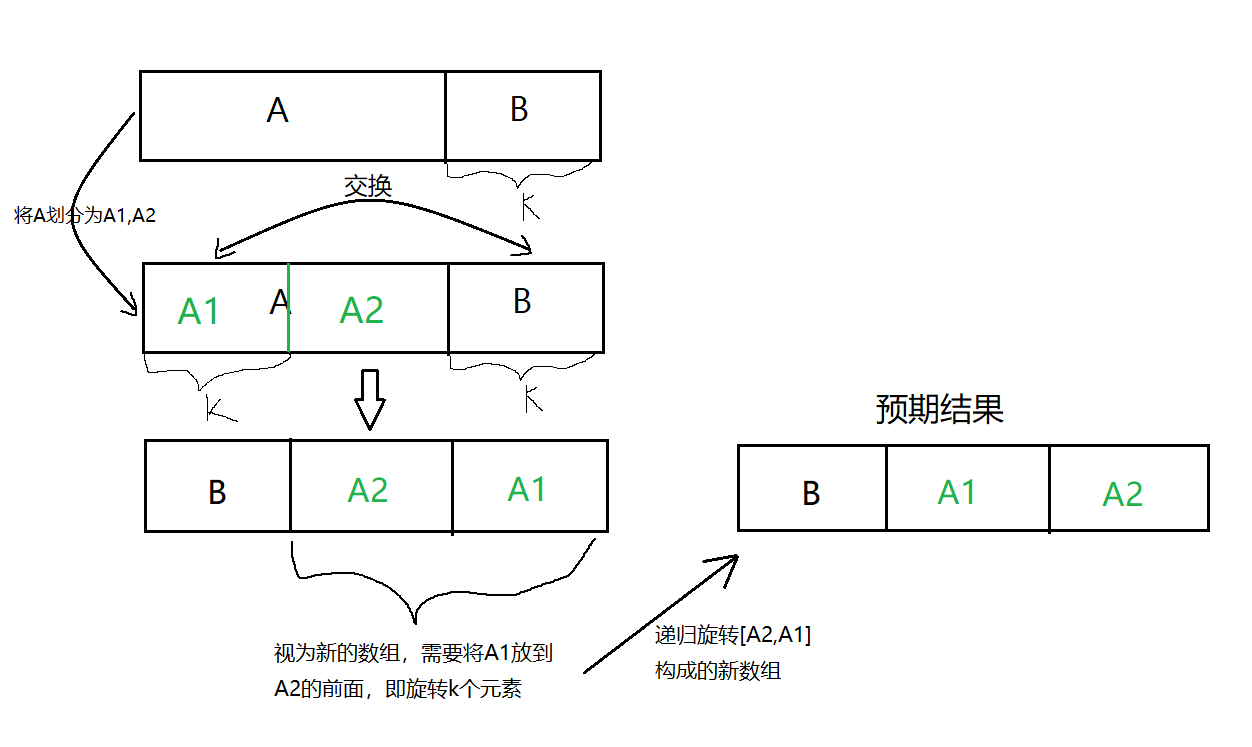
（为了方便讲解，我们先假设k<=n/2）

1.我们将数组划分为 [A，B]两段，其中B为后k个元素

2.那么我们想要实现的就是将B放到图中A1（数组的前k个元素）的位置

3.想要做到原地操作，那么容易想到：直接交换A1和B。这样B到了正确的位置，A1原始位置的数组也被保存了下来（放到了B原来的位置）

4.完成上一步操作后，我们得到的数组的形式是 [B，A2，A1]，而题目预期的结果应该是 [B，A1，A2]，可以发现 现在只要将由 [A2,A1] 构成的新数组进行题目中描述的旋转操作就可以转化为 [A1,A2] 了（形成递归）。

5.递归形成后，在新数组上调用我们的rotate函数就可以将新数组部分也完成旋转了。
(k>n/2的情况参考上面的方式也能推理出来，留给屏幕前的你来完成👍)

复杂度

时间复杂度:

假设共递归$t$次，每一次递归都会使得$m_i(iϵ[1,t])$个元素去到目标位置，这个操作的代价是$m_i$次交换操作，即每层递归为$O(m)$。所有的$m_i$加起来就等于总的元素个数$n$，即总的时间复杂度为 $O(n)$。

空间复杂度:

由于是在原地进行操作，故空间复杂度为 $O(1)$。但是其实递归的堆栈会消耗一定的空间。

Code

C++

class Solution {
public:void rotate(vector<int>& nums,int l,int r,int k){int n=r-l;k%=n;if(l+1>=r||!k)return;int i=l,j=0;if(k<=n/2)j=n-k+l;else j=k+l;while(j<r)swap(nums[i++],nums[j++]);if(k<=n/2)rotate(nums,l+k,r,k);else rotate(nums,l,r-n+k,2*k-n);return;}void rotate(vector<int>& nums, int k) {rotate(nums,0,nums.size(),k);return ;}
};