【C++】AVL树

一、概念

AVL树是一种平衡的二叉搜索树，它的特点是任何节点的两个子树的高度最大差别为1，也就是说它是高度平衡的。AVL树的查找、插入和删除的时间复杂度都是O（log n），但是插入和删除可能需要通过旋转来调整树的结构。AVL树是两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明的，达到降低树的高度，从而减少平均搜索长度的目的。

二、节点

template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data = T()): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _left;AVLTreeNode<T>* _right;AVLTreeNode<T>* _parent;T _data;int _bf;   // 节点的平衡因子
};

三、AVL树的插入

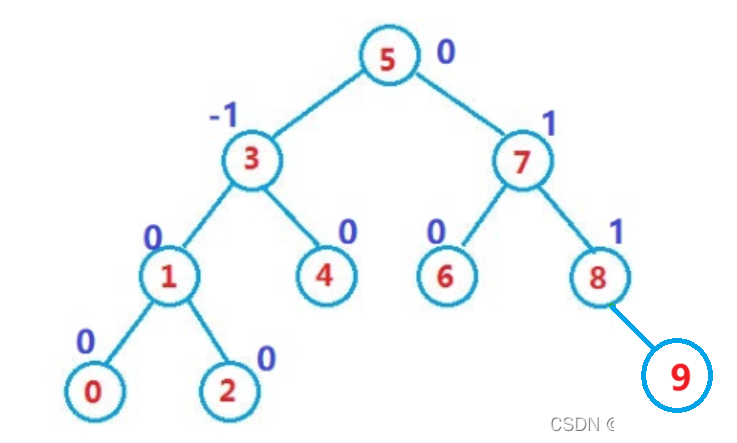
if (_root == nullptr){_root = new Node(data);return true;}Node* cur = _root;Node* parent = _root;//找到data节点插入的位置while (cur){if (data < cur->_data){parent = cur;cur = cur->_left;}else if (data > cur->_data){parent = cur;cur = cur->_right;}}//插入data节点Node* cur = new Node(data);if (data < parent->_data){cur->_parent = parent;parent->_left = cur;}else{cur->_parent = parent;parent->_right = cur;}

更新平衡因子bf： 

新增节点在左子树，父节点的平衡因子bf--；

新增节点在右子树，父节点的平衡因子bf++；

更新后：

1：父节点bf==0，父节点的子树高度不变，不必继续往上更新，插入结束。

2：父节点bf==1/-1，父节点的子树高度变化，必须往上更新

3：父节点bf==2/-2，父节点的子树违反规则，需要处理 

		while (parent){if (cur == parent->_left){parent->_bf--;}else if (cur == parent->_right){parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else{//旋转}}

1、子树高度不变

子树高度不变，则不会继续往上影响祖先

注：当新插入节点的父节点的平衡因子bf变为0，则说明父节点的子树高度不变，即不用再往上更新，插入结束。

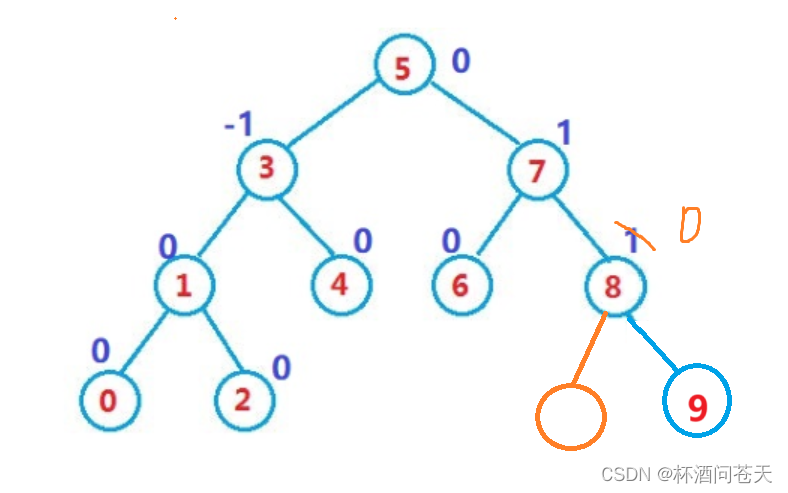
2、子树高度变化

子树高度变化，则会继续往上影响祖先

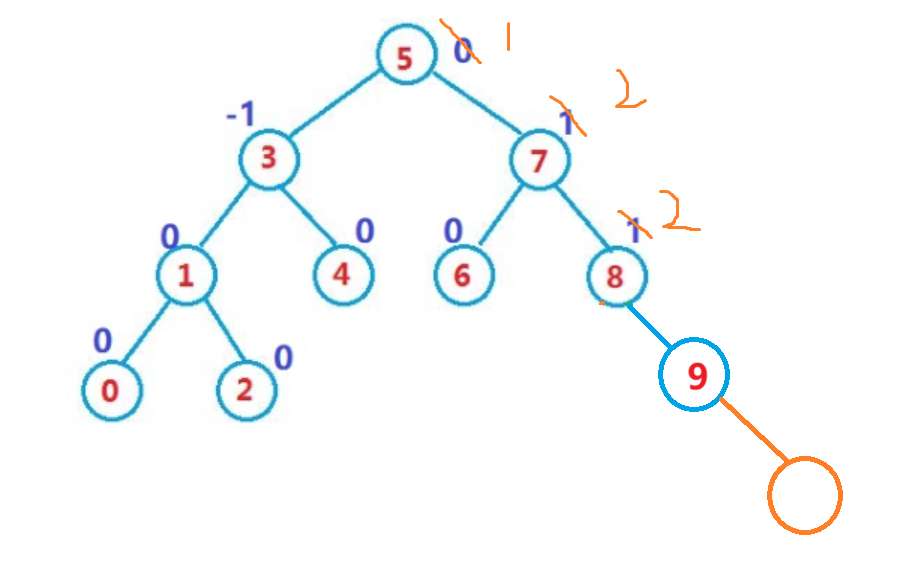
当平衡因子的绝对值大于1时，我们就需要对该子树进行调整。

AVL树的旋转

（1）右单旋

   →          

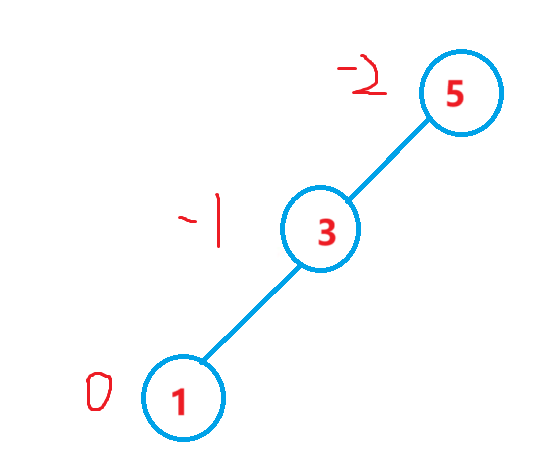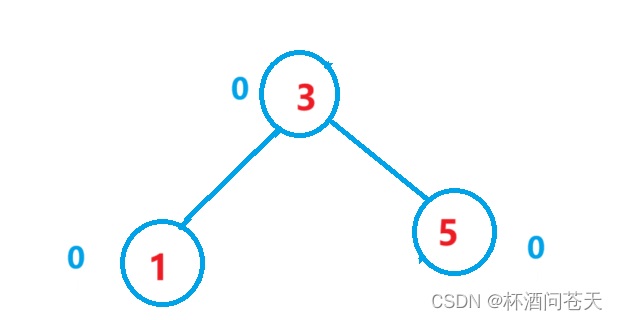
	void RotateR(Node* parent){Node* pprent = parent->_parent;Node* pl = parent->_left;Node* PRL = pl->_right;Node* PR = parent;//更新与上一节点的链接关系if (parent == _root){_root = pl;pl->_parent = nullptr;}else{if (pprent->_left == parent){pprent->_left = pl;}else{pprent->_right = pl;}pl->_parent = pprent;}pl->_right = PR;PR->_parent = pl;PR->_left = PRL;if(PRL)PRL->_parent = PR;pl->_bf = PR->_bf = 0;}

（2）左单旋

    →        

    →    

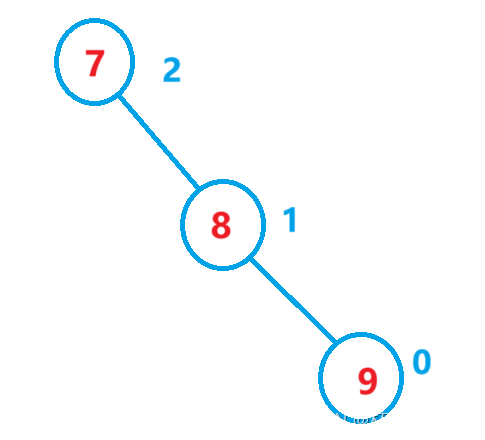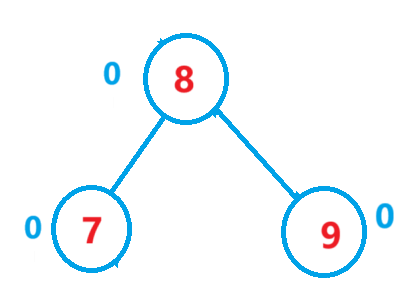
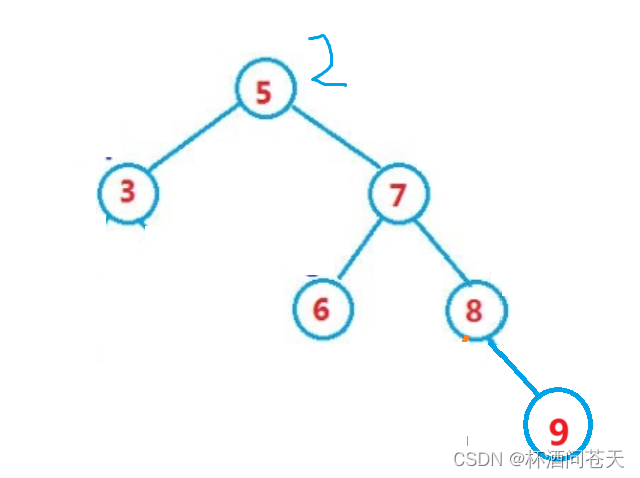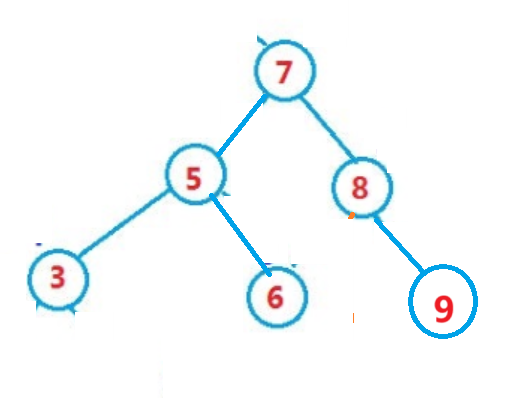
	void RotateL(Node* parent){Node* pprent = parent->_parent;Node* pr = parent->_right;Node* PLR = pr->_left;Node* PL = parent;//更新与上一节点的链接关系if (parent == _root){_root = pr;pr->_parent = nullptr;}else{if (pprent->_left == parent){pprent->_left = pr;}else{pprent->_right = pr;}pr->_parent = pprent;}pr->_left = PL;PL->_parent = pr;PL->_right = PLR;if(PLR)PLR->_parent = PL;//更新平衡因子pr->_bf = PL->_bf = 0;}

（3）左-右旋转

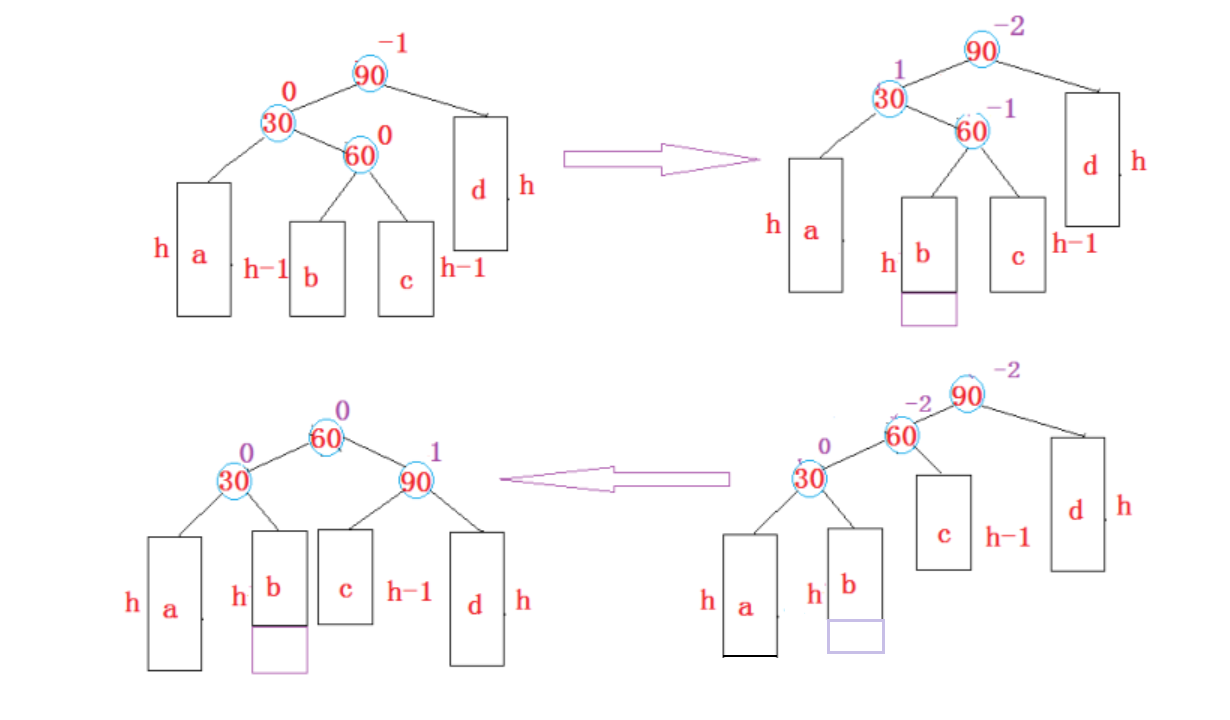
	// 左右双旋void RotateLR(Node* parent){Node* PR = parent;Node* PL = parent->_left;Node* P = PL->_right;int bf = P->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){PL->_bf = 0;PR->_bf = 0;P->_bf = 0;}else if(bf == 1){P->_bf = PR->_bf = 0;PL->_bf = -1;}else if (bf == -1){P->_bf = PL->_bf = 0;PR->_bf = 1;}//RotateL(parent->_left);//RotateR(parent);}

（4）右-左旋转

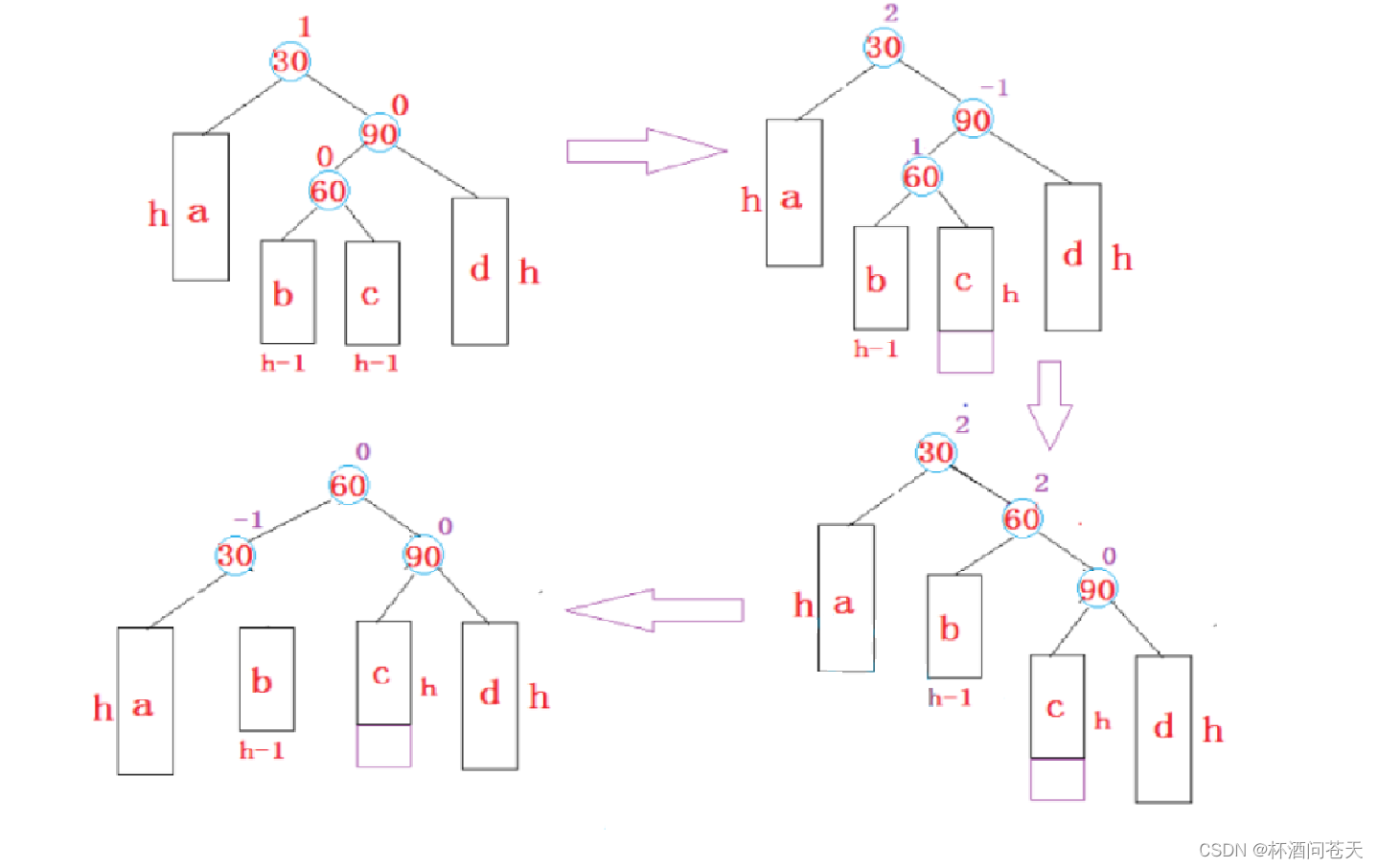
	// 右左双旋void RotateRL(Node* parent){Node* PL = parent;Node* PR = parent->_right;Node* P = PR->_left;int bf = P->_bf;RotateR(parent->_right);RotateL(parent);if(bf == 0){PL->_bf = 0;PR->_bf = 0;P->_bf = 0;}else if(bf == -1){P->_bf = PL->_bf = 0;PR->_bf = 1;}else if (bf == 1){P->_bf = PR->_bf = 0;PL->_bf = -1;}}

完整代码：

	bool Insert(const T& data){if (_root == nullptr){_root = new Node(data);return true;}Node* cur = _root;Node* parent = _root;//找到data节点插入的位置while (cur){if (data < cur->_data){parent = cur;cur = cur->_left;}else if (data > cur->_data){parent = cur;cur = cur->_right;}}//插入data节点cur = new Node(data);if (data < parent->_data){cur->_parent = parent;parent->_left = cur;}else{cur->_parent = parent;parent->_right = cur;}//更新平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else if (cur == parent->_right){parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else{//旋转//1.左单旋if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//2.右单旋if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//3.左-右旋转if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}//4.右-左旋转if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}//旋转过后无需再向上更新break;}}return true;}

四、AVL树的验证

	bool IsAVLTree(){return _IsAVLTree(_root);}// 根据AVL树的概念验证pRoot是否为有效的AVL树bool _IsAVLTree(Node* root){if (root == nullptr){return true;}int lefth = _Height(root->_left);int righth = _Height(root->_right);if (righth - lefth != root->_bf){cout << root->_data << ":bf false" << endl;return false;}return abs(lefth - righth) < 2 && _IsAVLTree(root->_left) && _IsAVLTree(root->_right);}size_t _Height(Node* root){if (root == nullptr){return 0;}int leftheight = _Height(root->_left);int rightheight = _Height(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;}