1.1 集合的初见
集合定义
什么是集合
- A set is a group of objects. (simplest way)
- By a set we mean any collection M into a whole of definite distinct objects m (which
- we called elements of M) of our perception or of our thought. (Cantor’s way)
- 集合是由指定范围内的满足给定条件的所有对象聚集在一起构成,每一个对象称为这个集合的元素。(In chinese)
- 外延公理+ 空集存在公理+ 无序对公理+ 并集公理+ 幂集公理+ 无穷公理+替换公理+ 正则公理+ 选择公理。(ZFC 公理化集合论)
集合的符号表示
用带或不带下标的大写英文字母表示集合:
用带或不带下标的小写英文字母表示元素:
属于关系
若a 是集合A 中的元素,则称a属于A,记为a ∈ A
若a 不是集合A 中的元素,则称a不属于A,记为a ∉2
集合表示方法:
枚举法
列出集合中的全部元素或者仅列出一部分元素,其余用省略号(...) 表示。

example:
A = {a; b; c; d}
B = {2; 4; 6; 8; 10; ...}
叙述法
通过刻画集合中元素所具备的某种性质或特性来表示一个集合。

文氏图(维恩图Venn)
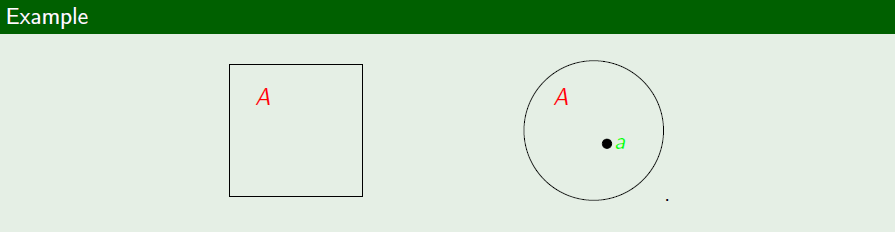
文氏图是利用平面上的点来做成对集合的图解方法。一般使用平面上的方形或圆形表示一个集合,而使用平面上的一个小圆点来表示集合的元素。
基数
定义:
集合A 中的元素个数称为集合的基数(base number),记为|A|
若一个集合的基数是有限的,称该集合为有限集(finite set)
若一个集合的基数是无限的,称该集合为无限集(infinite set)
例子















