目录
- 一、题目
- 二、思路
- 2.1 解题思路
- 2.2 代码尝试
- 2.3 疑难问题
- 三、解法
- 四、收获
- 4.1 心得
- 4.2 举一反三
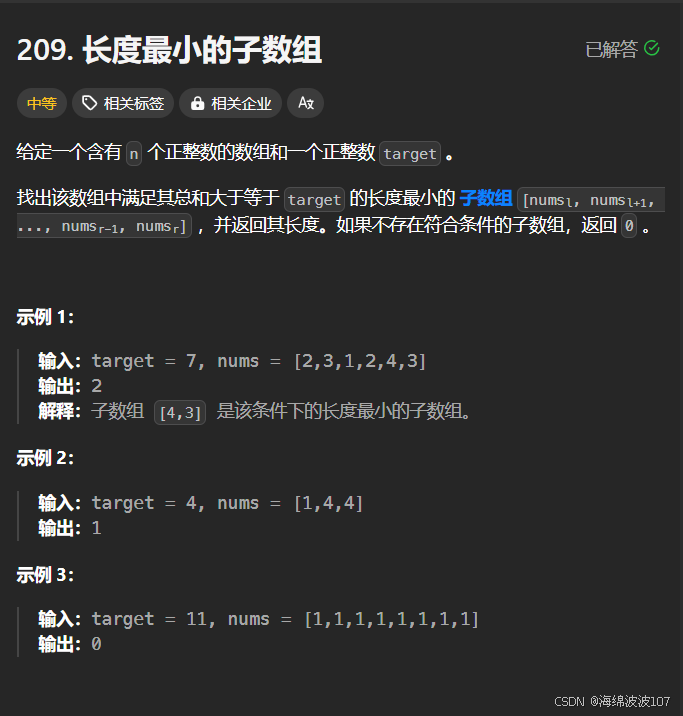
一、题目
二、思路
2.1 解题思路
尺蠖题模板思路
2.2 代码尝试
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int size=0;int maxsize=9999999;int sum=0;int j=0;int pos=0;int bound=0;for(int i=0;i<nums.size();i++){sum=nums[i];bound+=nums[i];if(sum>=target){return 1;}j=i+1;while(j<nums.size() && sum<target){sum+=nums[j];if(sum>=target){size=j-i+1;maxsize=min(maxsize,size);}j++;}}if(bound<target){return 0;}else{return maxsize;}}
};
2.3 疑难问题
感觉现在题目用贪心的思路,肯定能够暴力解出来。不过就是时间复杂度会高
三、解法
class Solution {
public:int minSubArrayLen(int s, vector<int>& nums) {int n = nums.size();if (n == 0) {return 0;}int ans = INT_MAX;int start = 0, end = 0;int sum = 0;while (end < n) {sum += nums[end];while (sum >= s) {ans = min(ans, end - start + 1);sum -= nums[start];start++;}end++;}return ans == INT_MAX ? 0 : ans;}
};作者:力扣官方题解
链接:https://leetcode.cn/problems/minimum-size-subarray-sum/solutions/305704/chang-du-zui-xiao-de-zi-shu-zu-by-leetcode-solutio/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
四、收获
4.1 心得
判断边界值可以采用判断表达式简化,就是这种整个字符串都达不到条件的情况

我的暴力法求解优化版,虽然还是会超时
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int maxsize=INT_MAX;int sum=0;int j=0;for(int i=0;i<nums.size();i++){sum=0;j=i;while(j<nums.size() && sum<target){sum+=nums[j];if(sum>=target){maxsize=min(maxsize,j-i+1);}j++;}}return maxsize==INT_MAX?0:maxsize;}
};
感觉很容易把可变滑动窗口写成暴力解法,这两者的区别在于,暴力解法每一次循环会把sum置为0重新计数,而可变窗口维护的是区间和,只会对sum做减法来收敛。不过两者都是两个for循环(左指和右指)。一般外面的都是for循环,而滑动窗口里面的while条件要注意,是维持窗口的满足条件,在这个满足条件下去收敛左边界。
4.2 举一反三
边界值:return 判断表达式
滑动窗口的内部while条件时维持窗口的满足条件














