欧派家居全屋定制价格多少钱一平_网站开发网站定制_北京网站_营销外包

一、红黑树的概念

1、红黑树的规则

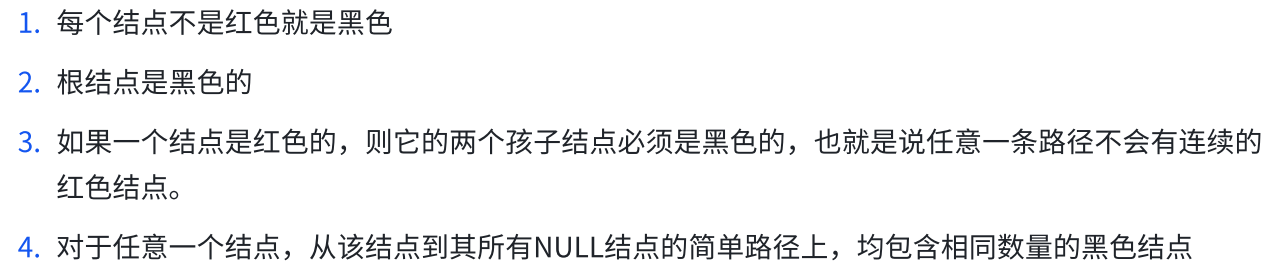
• 路径是根节点到空节点

2、红黑树的效率

二、红黑树的结构

// 枚举值表示颜色
enum Colour
{RED,BLACk
};// Key/vaule结构实现
template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<class K, class V>* _left;RBTreeNode<class K, class V>* _right;RBTreeNode<class K, class V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_paretn(nullptr){}
};template<class K,class V>
class RBTreeNode
{typedef RBTreeNode<K, V> Node;
public:
private:Node* _root = nullptr;
};

三、红黑树的插入

假设我们把新增结点标识为c(cur)，c的⽗亲标识为p(parent)，p的⽗亲标识为g(grandfather)，p的兄弟标识为u（uncle）。

1、变色

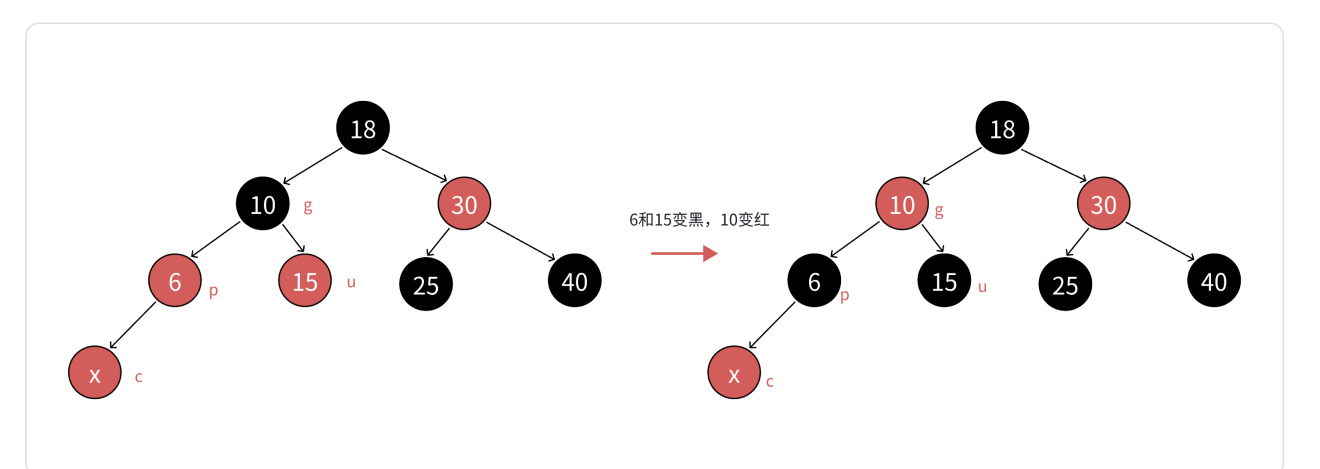
2、单旋+变色

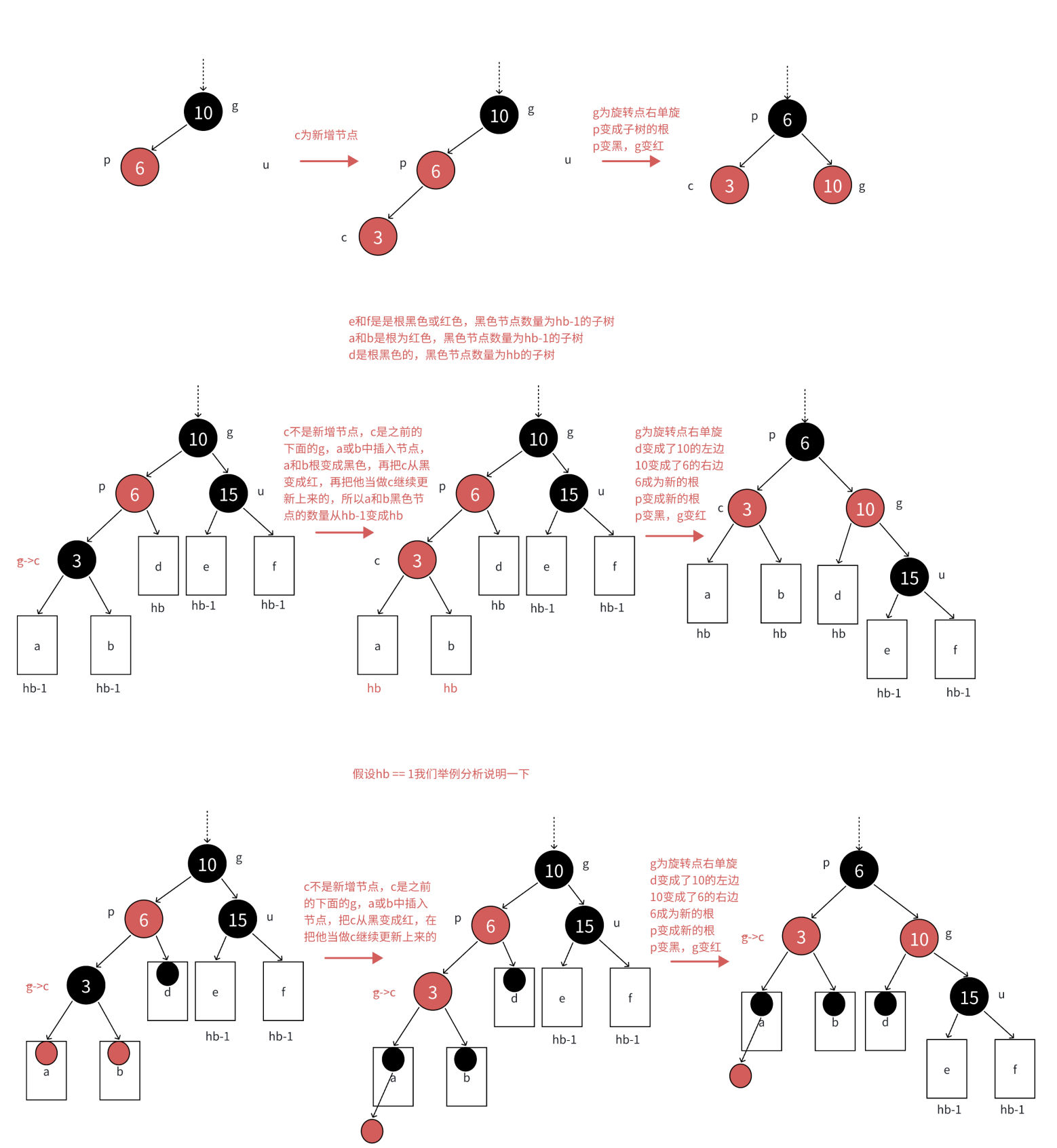
3、双旋+变色

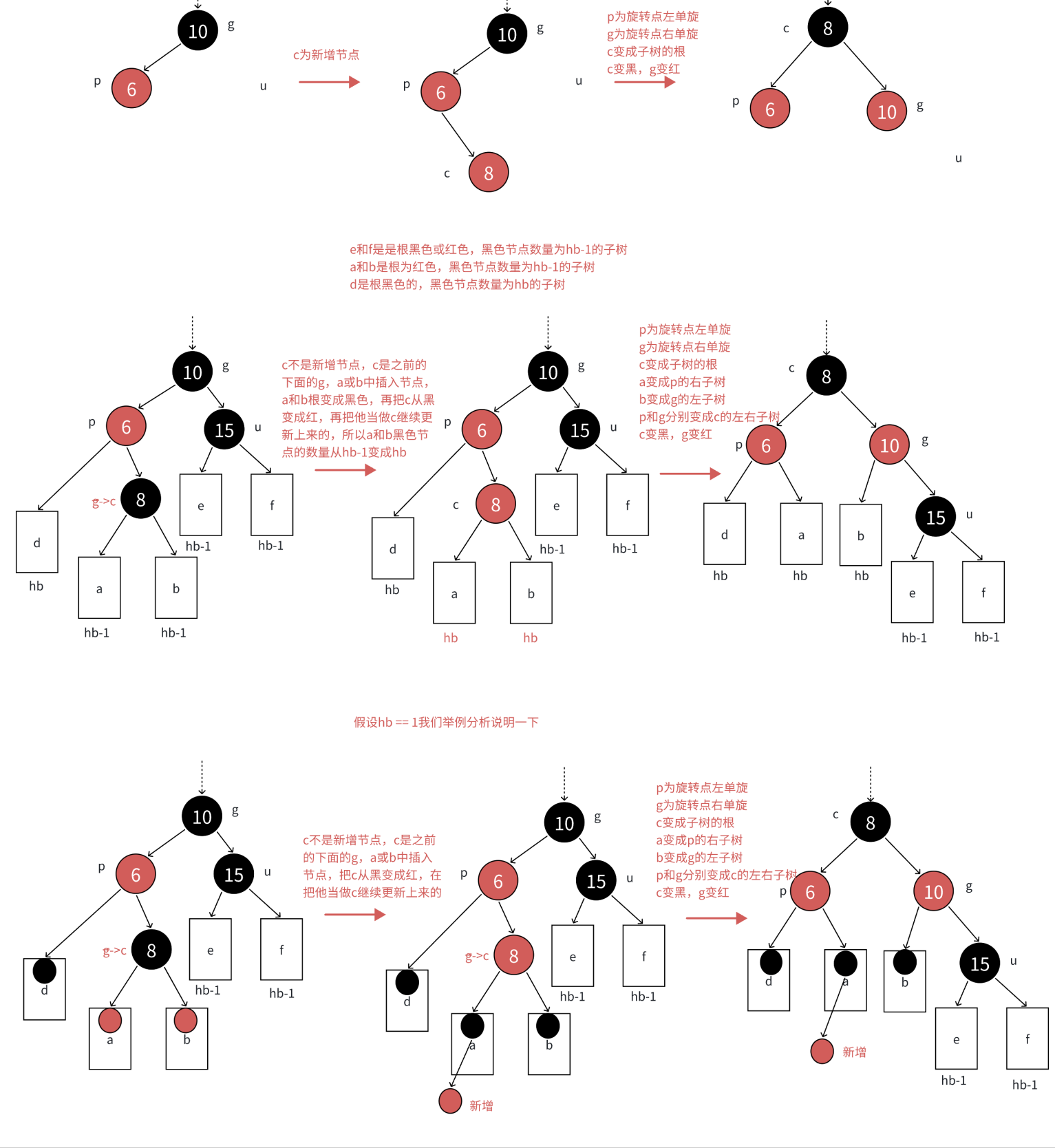
四、红黑树代码实现

#pragma once#include <iostream>
#include <utility>
#include <stdbool.h>
#include <vector>
#include <time.h>using namespace std;
// 枚举值表示颜色
enum Colour
{RED,BLACK
};// Key/vaule结构实现
template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode< K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr){}
};template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public://插入bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}elsereturn false;}cur = new Node(kv);cur->_col = RED;cur->_parent = parent;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;//   g//  p  u// 情况1：uncle 存在且为红if (uncle && uncle->_col == RED){//变色grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//继续向上处理cur = grandfather;parent = cur->_parent;}else // uncle 不存在，或存在且为黑{// 右单旋+变色//   g//  p  u//cif (parent->_left == cur){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;break;}else{// 左右双旋+变色//    g// p    u//  c RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;break;}}}else{Node* uncle = grandfather->_left;//   g//  u  p// 情况1：uncle 存在且为红if (uncle && uncle->_col == RED){//变色grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//继续向上处理cur = grandfather;parent = cur->_parent;}else // uncle 不存在，或存在且为黑{// 左单旋+变色//   g//  u  p//       cif (parent->_right == cur){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;break;}else{// 右左双旋+变色//    g// u    p//    cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;break;}}}}//根结点为黑色_root->_col = BLACK;return true;}//中序遍历void Inorder(){_Inorder(_root);cout << endl;}//检测是否是红黑树bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;int num = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)num++;if (cur->_left)cur = cur->_left;elsecur = cur->_right;}return Check(_root, 0, num);}bool Check(Node* root,int Bnum,int num){if (root == nullptr){if (Bnum == num)return true;elsereturn false;}if (root->_col == BLACK)Bnum++;else{if (root->_parent->_col == RED){cout << "存在连续红色结点" << ":" << root->_kv.first <<  endl;return false;}}bool left = true, right = true;if (root->_left)left = Check(root->_left, Bnum, num);if (!left)return false;if (root->_right)right = Check(root->_right, Bnum, num);return right;}int size(){return _size(_root);}int Height(){return _Height(_root);}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first > key){cur = cur->_left;}else if (cur->_kv.first < key){cur = cur->_right;}elsereturn cur;}return nullptr;}protected://红黑树的高度int _Height(Node* root){if (root == nullptr)return 0;int left = _Height(root->_left);int right = _Height(root->_right);return left > right  ? left + 1 : right + 1;}//有效数据个数int _size(Node* root){if (root == nullptr)return 0;return _size(root->_left) + _size(root->_right) + 1;}//右旋void RotateR(Node* root){Node* parent = root->_parent;Node* subL = root->_left;Node* subLR = subL->_right;if (root == _root){_root = subL;}else if (parent->_left == root){parent->_left = subL;}else{parent->_right = subL;}subL->_right = root;root->_left = subLR;if (subLR)subLR->_parent = root;root->_parent = subL;subL->_parent = parent;}//左旋void RotateL(Node* root){Node* parent = root->_parent;Node* subR = root->_right;Node* subRL = subR->_left;if (root == _root){_root = subR;}else if (parent->_left == root){parent->_left = subR;}else{parent->_right = subR;}subR->_left = root;root->_right = subRL;if (subRL)subRL->_parent = root;root->_parent = subR;subR->_parent = parent;}//中序遍历void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}private:Node* _root = nullptr;};