系列文章目录
第五章 1:Gated RNN(门控RNN)
第五章 2:梯度消失和LSTM
第五章 3:LSTM的实现
第五章 4:使用LSTM的语言模型
第五章 5:进一步改进RNNLM(以及总结)
文章目录
目录
系列文章目录
前言
一、LSTM的语言模型
前言
Time LSTM 层的实现完成了,现在我们来实现正题——语言模型。
一、LSTM的语言模型
这里实现的语言模型和上一章几乎是一样的,唯一的区别是,上一章使用 Time RNN层的地方这次使用Time LSTM层,如下图所示。
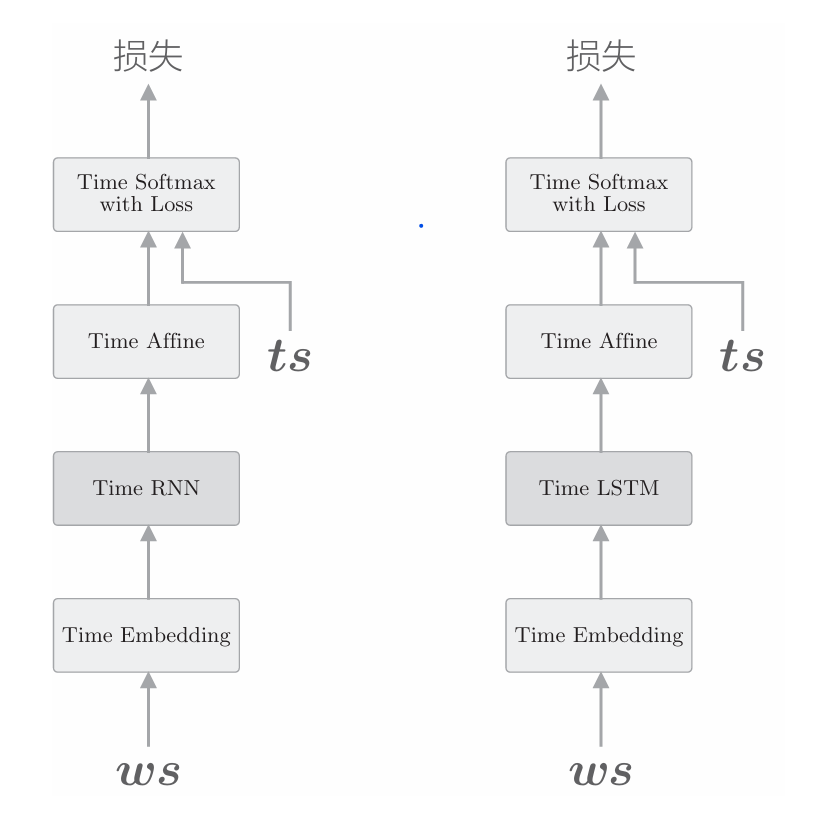
由上图可知,这里和上一章实现的语言模型的差别在于使用了 LSTM。我们将上图右图中的神经网络实现为Rnnlm类。Rnnlm类和上一章介绍的SimpleRnnlm类几乎相同,但是增加了一些新方法。下面给出使用 LSTM层实现的Rnnlm类的代码。
from common.time_layers import * # 这里面都是实现的TimeEmbedding, TimeLSTM,TimeAffine类
# 在前几章都可以找到from common.base_model import BaseModel"""
class BaseModel:def __init__(self):self.params, self.grads = None, Nonedef forward(self, *args):raise NotImplementedErrordef backward(self, *args):raise NotImplementedErrordef save_params(self, file_name=None):if file_name is None:file_name = self.__class__.__name__ + '.pkl'params = [p.astype(np.float16) for p in self.params]if GPU:params = [to_cpu(p) for p in params]with open(file_name, 'wb') as f:pickle.dump(params, f)def load_params(self, file_name=None):if file_name is None:file_name = self.__class__.__name__ + '.pkl'if '/' in file_name:file_name = file_name.replace('/', os.sep)if not os.path.exists(file_name):raise IOError('No file: ' + file_name)with open(file_name, 'rb') as f:params = pickle.load(f)params = [p.astype('f') for p in params]if GPU:params = [to_gpu(p) for p in params]for i, param in enumerate(self.params):param[...] = params[i]"""
# ------------------------------# 具体你可以问Deepseek,我这里只给出了核心代码
# ------------------------------
class Rnnlm(BaseModel):def __init__(self, vocab_size=10000, wordvec_size=100, hidden_size=100):V, D, H = vocab_size, wordvec_size, hidden_sizern = np.random.randn# 初始化权重embed_W = (rn(V, D) / 100).astype('f')lstm_Wx = (rn(D, 4 * H) / np.sqrt(D)).astype('f')lstm_Wh = (rn(H, 4 * H) / np.sqrt(H)).astype('f')lstm_b = np.zeros(4 * H).astype('f')affine_W = (rn(H, V) / np.sqrt(H)).astype('f')affine_b = np.zeros(V).astype('f')# 生成层self.layers = [TimeEmbedding(embed_W),TimeLSTM(lstm_Wx, lstm_Wh, lstm_b, stateful=True),TimeAffine(affine_W, affine_b)]self.loss_layer = TimeSoftmaxWithLoss()self.lstm_layer = self.layers[1]# 将所有的权重和梯度整理到列表中self.params, self.grads = [], []for layer in self.layers:self.params += layer.paramsself.grads += layer.gradsdef predict(self, xs):for layer in self.layers:xs = layer.forward(xs)return xsdef forward(self, xs, ts):score = self.predict(xs)loss = self.loss_layer.forward(score, ts)return lossdef backward(self, dout=1):dout = self.loss_layer.backward(dout)for layer in reversed(self.layers):dout = layer.backward(dout)return doutdef reset_state(self):self.lstm_layer.reset_state()def save_params(self, file_name="Rnnlm.pkl"):with open(file_name, 'wb') as f:pickle.dump(self.params, f)def load_params(self, file_name="Rnnlm.pkl"):with open(file_name, 'rb') as f:self.params = pickle.load(f)Rnnlm 类将到Softmax 层为止的处理实现为predict()方法,这个方法在后面章节进行文本生成时还会用到。此外,该类还添加了用于读写参数的save_params() 和 load_params() 方法。剩下的实现与上一章的SimpleRnnlm 类相同。
下面,我们在PTB数据集上学习这个网络。这次我们使用PTB数据 集的所有训练数据进行学习(上一章中只使用了PTB数据集的一部分),代码如下所示
# coding: utf-8
import sys
sys.path.append('..')
from common.optimizer import SGD
from common.trainer import RnnlmTrainer
from common.util import eval_perplexity
from dataset import ptb
from rnnlm import Rnnlm# 设定超参数
batch_size = 20
wordvec_size = 100
hidden_size = 100 # RNN的隐藏状态向量的元素个数
time_size = 35 # RNN的展开大小
lr = 20.0
max_epoch = 4
max_grad = 0.25# 读入训练数据
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_test, _, _ = ptb.load_data('test')
vocab_size = len(word_to_id)
xs = corpus[:-1]
ts = corpus[1:]# 生成模型
model = Rnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
trainer = RnnlmTrainer(model, optimizer)# 1.应用梯度裁剪进行学习
trainer.fit(xs, ts, max_epoch, batch_size, time_size, max_grad,eval_interval=20)
trainer.plot(ylim=(0, 500))# 2.基于测试数据进行评价
model.reset_state()
ppl_test = eval_perplexity(model, corpus_test)
print('test perplexity: ', ppl_test)# 3.保存参数
model.save_params()
这里给出的代码和上一章的代码有很多相同的地方, 因此这里重点介绍不同的地方。首先,代码1处使用RnnlmTrainer类进行模型的学习。RnnlmTrainer 类的fit() 方法求模型的梯度,更新模型的参数。 另外,在方法内部,通过指定max_grad参数,从而应用梯度裁剪。顺便说一 下,fit() 方法内部进行的实现如下所示(伪代码)

我们在第五章第四节(自然语言处理(16:(第五章1.)Gated RNN)-CSDN博客)将梯度裁剪实现为了clip_grads(grads, max_grad),这里使用该方法进行梯度裁剪。
另外,通过1.处的fit()方法的参数eval_interval=20,每20次迭代对 困惑度进行1次评价。因为这次的数据量很大,所以没有对每个epoch进行 评价,而是每20次迭代评价1次。后面我们会将评价结果用plot()方法绘 制成图。 在学习结束后,在代码2.处使用测试数据对困惑度进行评价。这里需要 注意的是,此时需要先重置模型的状态(LSTM的隐藏状态和记忆单元)。 此外,因为评价困惑度的函数eval_perplexity()在common/util.py中已经实 现,所以直接使用即可。 最后,在代码3.处将学习好的参数保存到外部文件。在下一章生成句子 时,将会使用这些学习好的权重参数。 以上就是RNNLM的学习代码。执行代码后,在终端上会输出下图的结果(我在CPU上运行,比较慢,但是数据少,我们可以等一会(约10分钟))
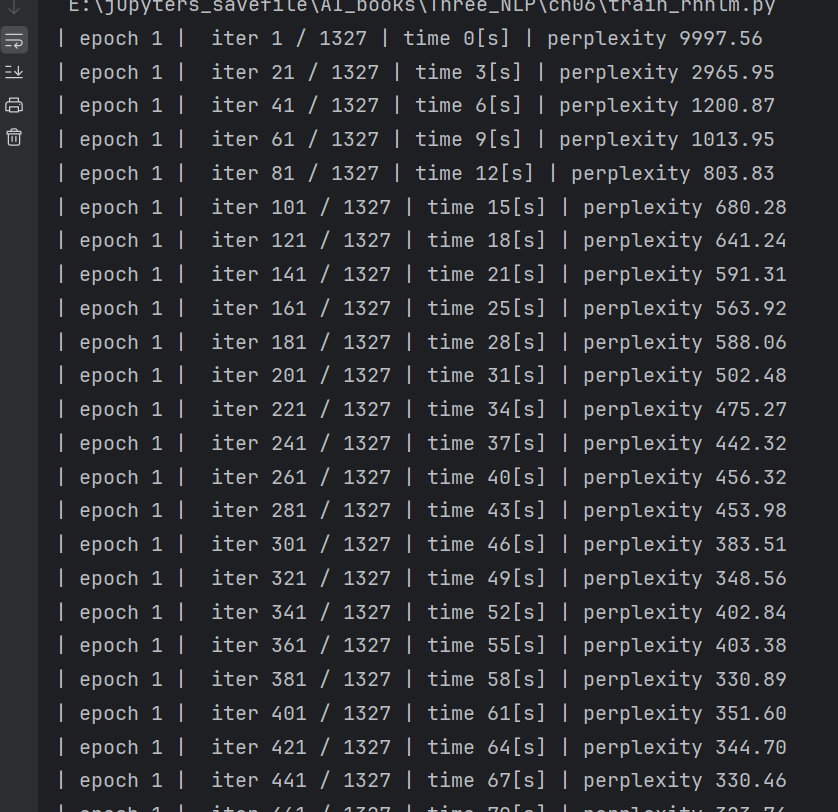
每20次迭代输出1次困惑度的值。我们来看一下结果, 刚开始的困惑度为10000.84,这意味着下一个单词的候选个数能减少到 10 000 个左右。因为这次数据集的词汇量是10 000个,所以这是什么也没 学习的状态,相当于猜测。但是随着学习的进行,困惑度开始变好。实际上,当迭代超过300次时,困惑度已经降到了400以下。现在,我们看一下困惑度的演变图,如下图所示。
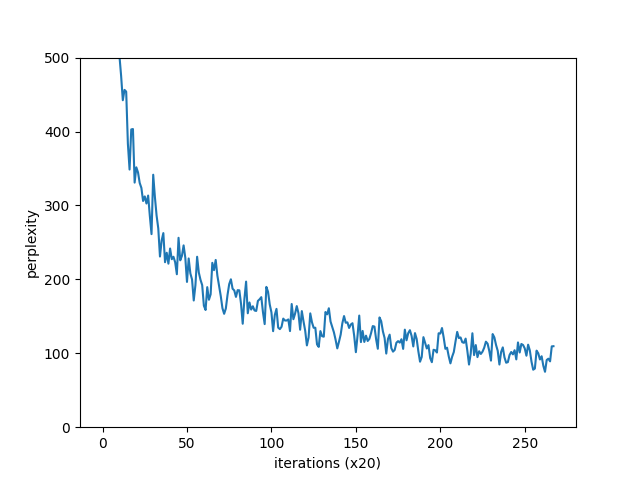
在这次的实验中,一共进行了4个epoch的学习(按迭代来算,相当于1327 * 4 次)。如图所示,困惑度顺利下降,最终达到100左右。基于最终的测试数据的评价(源代码2.处)结果为136.07...。该结果在每次执行时都不相同,但是都在135前后。换句话说,我们的模型成长到了能将下一个单词的候选个数(从10 000个)缩小到136个左右的水平。 那么,136这样的困惑度在实践中是什么水平呢?说实话,这并不是一个很好的结果。在2017年的一个研究中,PTB数据集上的困惑度已经降到了60以下。我们的模型还有很大的改进空间,下面我们就来进一步改进现有的RNNLM。














