一、DFS(深度优先搜索)—— 适合 "一条路走到黑" 的场景
典型特征:需要探索所有可能性、寻找存在性解、处理排列组合问题
🌰 例如:
想象你在玩 密室逃脱,面前有3扇门:
- 选择第一扇门 → 进入后又有2扇门 → 继续选第一扇 → 直到找到出口 或 死胡同
- 若死胡同就 原路返回,尝试之前没选的门
💻 常见题型:
| 场景 | 例题 | 为什么用DFS |
| 排列组合 | 全排列、子集生成 | 需要遍历所有可能的组合 |
| 连通性检测 | 岛屿数量、迷宫能否走出 | 一条路径走到底检查连通 |
| 回溯问题 | 八皇后、数独 | 尝试性填入→失败回退 |
| 存在性判断 | 二叉树中是否存在某路径和 | 只需找到一个解即可 |
代码特征:递归结构明显,常有 visited 标记 和 回溯操作
二、BFS(广度优先搜索)—— 适合 "层层递进找最短" 的场景
典型特征:需要最短路径、层级关系分析、最小步骤问题
🌰 例如:
想象 火灾蔓延:
- 火源同时向四周所有方向扩散
- 第一秒烧毁周围1米,第二秒烧毁2米...
- 最先到达出口 的路径就是最短逃生路径
💻 常见题型:
| 场景 | 例题 | 为什么用BFS |
| 最短路径 | 迷宫最短步数、单词接龙 | 首次到达即最短 |
| 层级遍历 | 二叉树层序遍历、社交网络N度好友 | 天然按层处理 |
| 状态最小转换 | 华容道最少步数、魔方还原 | 每一步状态作为一层 |
| 拓扑排序 | 课程安排依赖顺序 | 入度归零的层级推进 |
代码特征:使用队列,常有 distance 或 level 记录层数
三、对照表:5秒决策法
| 条件 | 选择算法 |
| 问题包含 "最短"、"最少" 等关键词 | → BFS |
| 需要 所有可能解 或 存在性判断 | → DFS |
| 数据规模小(如N≤20) | → DFS |
| 数据规模大 但 求最短路径 | → BFS+剪枝 |
| 树/图的 层序遍历 需求 | → BFS |
| 出现 递归回溯 特征 | → DFS |
四、实战技巧
- DFS优化:记忆化搜索、剪枝(提前终止不可能分支)
- BFS变种:双向BFS(从起点和终点同时扩散,加速搜索)
- 混合使用:比如IDA(迭代加深搜索,结合DFS空间+BFS层级)
例题测试:
- 走迷宫求能否走出 → DFS
- 走迷宫求最短路径 → BFS
- 数独求解 → DFS+剪枝
- 社交网络三度好友推荐 → BFS
记住这个口诀:"深搜所有可能,广搜最短一层"。比赛时先快速判断问题类型,再选择武器库中的合适算法

代码的话,我们可以以求岛屿最大面积的那一题的代码为例,来进行一个对比
[Lc15_bfs+floodfill] 图像渲染 |岛屿数量 |岛屿的最大面积| 被围绕的区域
[Lc5_dfs+floodfill]岛屿的最大面积(&传参) | 被围绕的区域
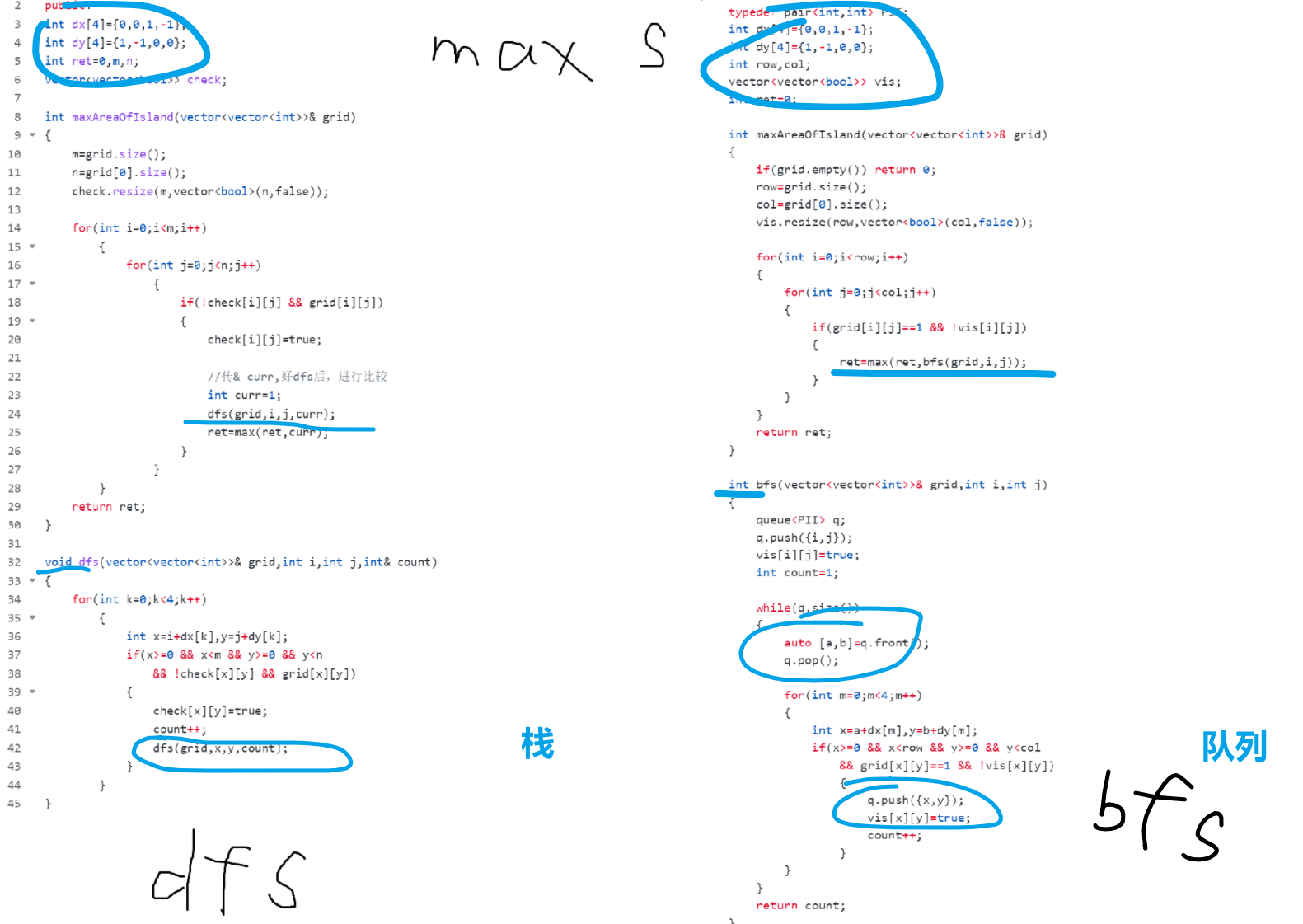
- 对了,还有一种 BFS替代DFS 的情况
在预见的是 大规模矩阵 的情况下,使用 队列 实现广度优先搜索,避免栈溢出风险














