上海十大活动策划公司_诸城网络推广公司_友链是什么_网时代教育培训机构怎么样

距上次打CF已经有将近5年的时间了，回忆涌上心头，赶紧来试试找找感觉

A. Olympiad Date

思路：真的是很久没做题了，理解题意理解了好久。最后发现，其实就是要收集20250103这几个数字，按顺序取数，判断一下最早能极其的位置即可。那么直接模拟一下

/*
Author Owen_Q
*/
#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 5;#define ll long longint main() {ios_base::sync_with_stdio(false), cin.tie(nullptr);int t;cin >> t;while (t--) {map<int, int> olympiad = {{0, 3}, {1, 1}, {2, 2}, {3, 1}, {5, 1}};int n;cin >> n;int a[N];int re = 0;int count = 8;for (int i = 1; i <= n; i++) {cin >> a[i];}for (int i = 1; i <= n; i++) {if (olympiad[a[i]]>0) {count --;olympiad[a[i]]--;if (count == 0) {re = i;break;}}}cout << re << '\n';}return 0;
}

B. Team Training

思路：组队问题，n个人组队，队伍分数为人数*队内最小分数人，给定最小队伍分数，求最少组几队。很明显，高分人员优先组队，低分人员就是弱鸡累赘。因此按人员分数排序，成对即换队，避免队伍整体分数降低，就是个最优策略。

/*
Author Owen_Q
*/
#include <bits/stdc++.h>using namespace std;const int N = 2e5 + 5;#define ll long longint main() {ios_base::sync_with_stdio(false), cin.tie(nullptr);int t;cin >> t;while (t--) {int n, x;cin >> n >> x;int a[N];for (int i = 0; i < n; i++) {cin >> a[i];}sort(a, a + n, greater<int>());int re = 0;int num = 0;for (int i = 0; i < n; i++) {num ++;if (num * a[i] >= x) {re ++;num = 0;}}cout << re << endl;}return 0;
}

C. Combination Lock

思路：这题就是个典型的策略题，要求每次旋转都只命中一个数，那么直接按照命中的数去生成串即可。其实可以不关注样例，直接自行选一个简单的策略为每次转一个就往前匹配一位，那么就可以按照数字从大到小排序，从末尾开始生成，每次向前移动两格，循环往复刚好可以匹配成功。最后，注意特判一下，只有奇数位数才能生成成功，偶数位数直接跳过即可。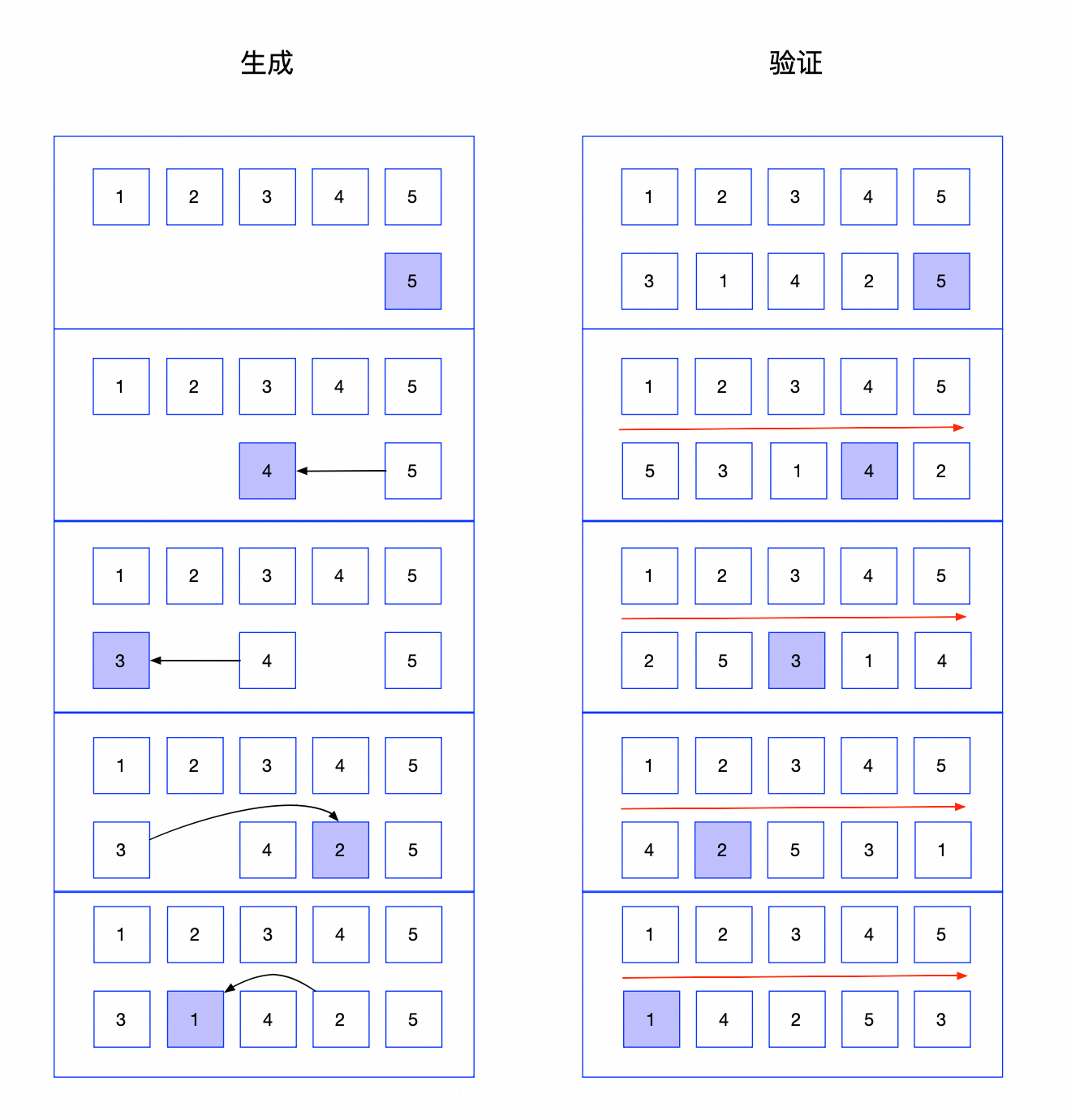

/*
Author Owen_Q
*/
#include <bits/stdc++.h>using namespace std;const int N = 2e5 + 5;#define ll long longint main() {ios_base::sync_with_stdio(false), cin.tie(nullptr);int t;cin >> t;while (t--) {int n;cin >> n ;if (n % 2 == 0) {cout << -1 << '\n';continue;}int a[N];int pos = n-1;int now = n;while (now) {a[pos] = now;pos -= 2;if (pos < 0) {pos += n;}now--;}cout << a[0];for (int i = 1; i < n; i++) {cout << " " << a[i];}cout << '\n';}return 0;
}

D. Place of the Olympiad

思路：在 $n\times m$ 的矩形区域横放 $k$ 个区域的凳子，求所需准备的最长凳子。首先由于是 $n$ 行区域填充 $k$ 个区域，那么最多的一行可能需要填充 $\left \lceil \frac{k}{n} \right \rceil$ 个区域。于是问题简化为，在 $m$ 个区域填充 $\left \lceil \frac{k}{n} \right \rceil$ 个区域，求最长区域。脑袋一下卡住了，打了个表貌似也没什么新发现

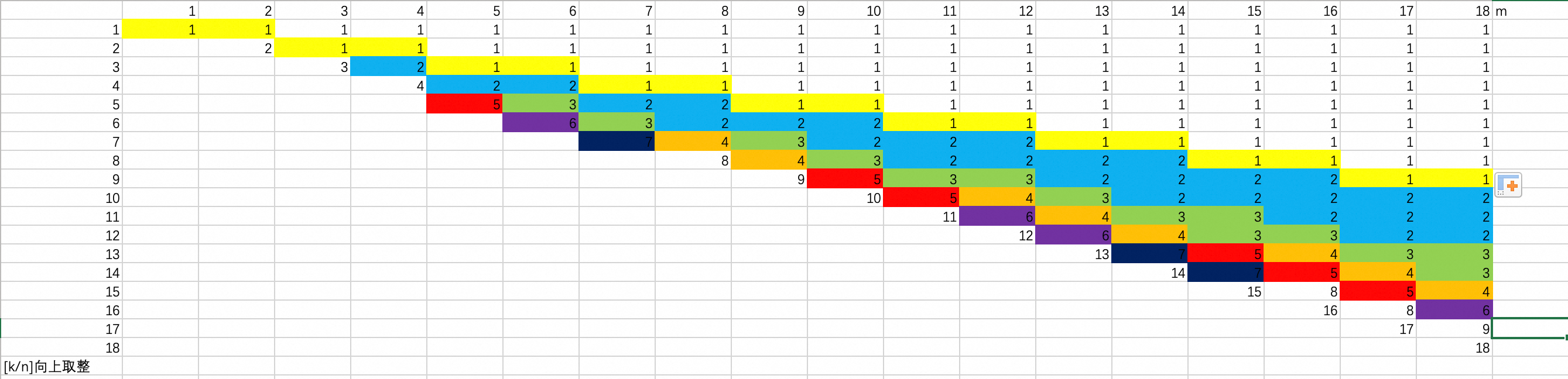
还是重新回归题意，偶然间发现，其实被简化后的一维题意和简化前的二维题意有异曲同工之妙。

简化前后对比
	原题意	重新解读后	结果
简化前	$n$ 行区域填充 $k$ 个区域	$k$ 个区域分成 $n$ 组	$\left \lceil \frac{k}{n} \right \rceil$
简化后	在 $m$ 个区域填充 $\left \lceil \frac{k}{n} \right \rceil$ 个区域	$\left \lceil \frac{k}{n} \right \rceil$ 个区域分成 $m-\left \lceil \frac{k}{n} \right \rceil+1$ 组	$\left \lceil \frac{\left \lceil\frac{k}{n}\right \rceil}{m-\left \lceil \frac{k}{n} \right \rceil+1} \right \rceil$

简化后重新解读过程：填充 $\left \lceil \frac{k}{n} \right \rceil$ 个区域说明有 $m-\left \lceil \frac{k}{n} \right \rceil$ 个区域的空格，那么就说明填充区域被分成了 $m-\left \lceil \frac{k}{n} \right \rceil+1$ 组

于是一切豁然开朗，最终结果即为 $\left \lceil \frac{\left \lceil\frac{k}{n}\right \rceil}{m-\left \lceil \frac{k}{n} \right \rceil+1} \right \rceil$

/*
Author Owen_Q
*/
#include <bits/stdc++.h>using namespace std;const int N = 1e9 + 5;#define ll long longint main() {ios_base::sync_with_stdio(false), cin.tie(nullptr);int t;cin >> t;while (t--) {int n, m, k;cin >> n >> m >> k;int mDivPiece = (k / n + (k % n ? 1 : 0));int mBlankPiece = m - mDivPiece;int mDivPart = mBlankPiece + 1;int re = mDivPiece / mDivPart + (mDivPiece % mDivPart ? 1 : 0);cout << re << '\n';}return 0;
}

E. Interesting Ratio

思路： $F(a,b)=\frac{lcm(a,b)}{gcd(a,b)}$ ，

假设 $a=gcd(a,b)\times p$ ， $b=gcd(a,b)\times q$ ， $a < b ==> p < q$

那么 $lcm(a,b)=p\times q \times gcd(a,b)$ ， $F(a,b)=p\times q$

要想让 $F(a,b)$ 为素数，那么 $p$ 一定为1， $q$ 一定为素数。

于是一切都豁然开朗了， $a$ 是任意数， $b$ 是 $a$ 的素数倍数

打个表验证一下，完全没问题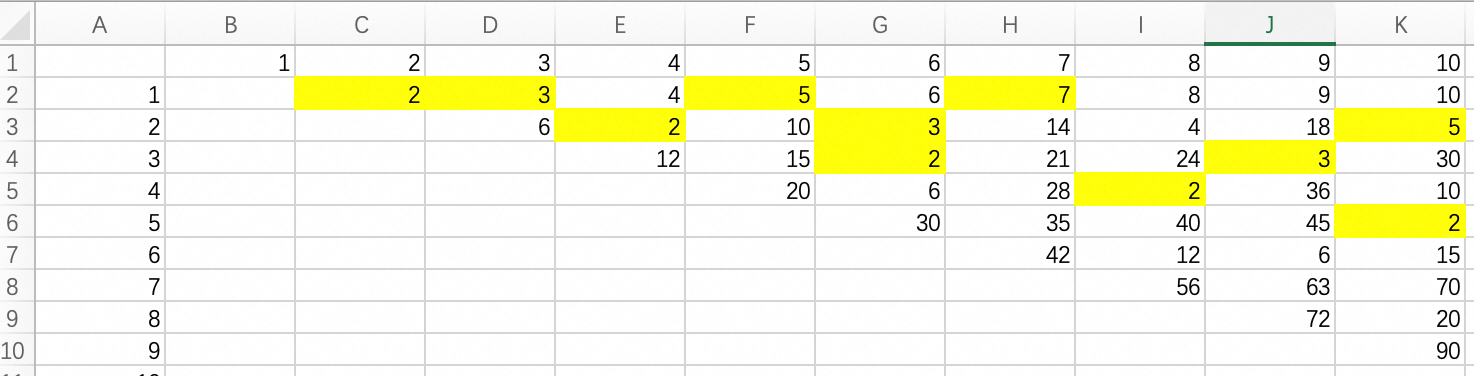

于是题目就简化为求 $n$ 以内所有 $b= a\times prime<n$ 的个数。这就需要用到素数筛了，将 $n$ 以内的所有素数预处理出来，再进行计算即可。

说到素数筛，目前最主流的就是埃氏筛和欧拉筛。

埃氏筛十分好理解，针对每个素数，其任意倍数一定不是素数，于是遍历所有数，将其倍数标记为非素数，即可获得素数集合，这种算法的复杂度为 $O(nloglogn)$ 。但是由于其筛选过程中，每个合数都会被其所有的质因数重复筛选。

而欧拉筛则恰好避免了这个问题，将复杂度成功降到 $O(n)$ 。那我们就来看一下欧拉筛。

欧拉筛相比于埃氏筛，有两个优化点

1.欧拉筛只将当前数与已知素数倍数进行相乘筛选

2.若当前数是判别素数的倍数，则不继续进行判断。

第一点很好理解，避免大数小数重复筛选

第二点就可能要思考一下了。

我们假设判别素数为 $p$ ，当前数为 $r\times p$ ，那么当前筛选的数为 $r \times p \times p$ ，那么下一个被筛选的数为 $r \times p \times q$ ，其中 $q$ 为 $p$ 之后的下一个素数。针对 $r \times p \times q$ ，当筛选到 $r \times q$ 这个数的时候，其一定会被更小的质因数 $p$ 筛掉，所以此处就不用再重复筛选了。

最后上代码~

/*
Author Owen_Q
*/
#include <bits/stdc++.h>using namespace std;const int N = 1e3 + 5;
const int M = 1e7 + 5;#define ll long longint n[N];
bool notPrime[M];
int prime[M];int main() {ios_base::sync_with_stdio(false), cin.tie(nullptr);int t;cin >> t;int maxn = 0;for (int i = 0; i < t; i++) {cin >> n[i];if (n[i] > maxn) {maxn = n[i];}}int primeCount = 0;for (int numi = 2; numi <= maxn; numi++) {if (!notPrime[numi]) {prime[primeCount++] = numi;}for (int primePosj = 0; primePosj < primeCount; primePosj++) {ll nowNum = (ll) prime[primePosj] * (ll) numi;if (nowNum > maxn) {break;}notPrime[nowNum] = true;if (numi % prime[primePosj] == 0) {break;}}}for (int testi = 0; testi < t; testi++) {int count = 0;for (int numj = 1; numj < n[testi]; numj++) {for (int primePosk = 0; primePosk < primeCount; primePosk++) {ll f = (ll) numj * (ll) prime[primePosk];if (f > n[testi]) {break;}count++;}}cout << count << '\n';}return 0;
}