网络营销是借助于什么营销手段_简述网页制作步骤_官网建站多少钱_重庆seo标准

A - delete .

Problem Statement

You are given a string $S$ consisting of lowercase English letters and ..
Find the string obtained by removing all . from $S$.

Constraints

$S$ is a string of length between $1$ and $100$, inclusive, consisting of lowercase English letters and ..

Input

The input is given from Standard Input in the following format:

$S$

Output

Print the string obtained by removing all . from $S$.

Sample Input 1

.v.

Sample Output 1

v

Removing all . from .v. yields v, so print v.

Sample Input 2

chokudai

Sample Output 2

chokudai

There are cases where $S$ does not contain ..

Sample Input 3

...

Sample Output 3

There are also cases where all characters in $S$ are ..

Solution

具体见文末视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;string s;signed main() {cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> s;for (auto v : s)if (v != '.') cout << v;cout << endl;return 0;
}

B - 3^A

Problem Statement

You are given a positive integer $M$.
Find a positive integer $N$ and a sequence of non-negative integers $A=(A_1,A_2,\dots ,A_N)$ that satisfy all of the following conditions:
$1\le N\le 20$
$0\le A_i\le 10$ $(1\le i\le N)$
$\sum _{i=1}^N{3}^{A_i}=M$
It can be proved that under the constraints, there always exists at least one such pair of $N$ and $A$ satisfying the conditions.

Constraints

$1\le M\le 10^5$

Input

The input is given from Standard Input in the following format:

$M$

Output

Print $N$ and $A$ satisfying the conditions in the following format:

$N$
$A_1$ $A_2$ $\ldots$ $A_N$

If there are multiple valid pairs of $N$ and $A$, any of them is acceptable.

Sample Input 1

6

Sample Output 1

2
1 1

For example, with $N=2$ and $A=(1,1)$, we have $\sum _{i=1}^N{3}^{A_i}=3+3=6$, satisfying all conditions.
Another example is $N=4$ and $A=(0,0,1,0)$, which also satisfies the conditions.

Sample Input 2

100

Sample Output 2

4
2 0 2 4

Sample Input 3

59048

Sample Output 3

20
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9

Note the condition $1\le N\le 20$.

Solution

具体见文末视频。

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;signed main() {cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int n;cin >> n;std::vector<int> bit;while (n) {bit.push_back(n % 3);n /= 3;}std::vector<int> res;for (int i = bit.size() - 1; i >= 0; i --)for (int j = bit[i]; j >= 1; j --) res.push_back(i);cout << res.size() << endl;for (auto v : res)cout << v << " ";cout << endl;return 0;
}

C - Count ABC Again

Problem Statement

You are given a string $S$ of length $N$. You are also given $Q$ queries, which you should process in order.
The $i$-th query is as follows:
Given an integer $X_i$ and a character $C_i$, replace the $X_i$-th character of $S$ with $C_i$. Then, print the number of times the string ABC appears as a substring in $S$.
Here, a substring of $S$ is a string obtained by deleting zero or more characters from the beginning and zero or more characters from the end of $S$.

For example, ab is a substring of abc, but ac is not a substring of abc.

Constraints

$3\le N\le 2\times 10^5$
$1\le Q\le 2\times 10^5$
$S$ is a string of length $N$ consisting of uppercase English letters.
$1\le X_i\le N$
$C_i$ is an uppercase English letter.

Input

The input is given from Standard Input in the following format:

$N$ $Q$
$S$
$X_1$ $C_1$
$X_2$ $C_2$
$\vdots$
$X_Q$ $C_Q$

Output

Print $Q$ lines.
The $i$-th line $(1\le i\le Q)$ should contain the answer to the $i$-th query.

Sample Input 1

7 4
ABCDABC
4 B
3 A
5 C
4 G

Sample Output 1

2
1
1
0

After processing each query, $S$ becomes as follows.
After the first query: $S=$ ABCBABC. In this string, ABC appears twice as a substring.
After the second query: $S=$ ABABABC. In this string, ABC appears once as a substring.
After the third query: $S=$ ABABCBC. In this string, ABC appears once as a substring.
After the fourth query: $S=$ ABAGCBC. In this string, ABC appears zero times as a substring.

Sample Input 2

3 3
ABC
1 A
2 B
3 C

Sample Output 2

1
1
1

There are cases where $S$ does not change through processing a query.

Sample Input 3

15 10
BBCCBCACCBACACA
9 C
11 B
5 B
11 B
4 A
8 C
8 B
5 B
7 B
14 B

Sample Output 3

0
0
0
0
1
1
2
2
1
1

Solution

具体见文末视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;signed main() {cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int n, q;string s;cin >> n >> q >> s;auto count = [&](int x) -> int {int cnt = 0;if (x + 2 < n) cnt += (s[x] == 'A' && s[x + 1] == 'B' && s[x + 2] == 'C');if (x > 0 && x + 1 < n) cnt += (s[x - 1] == 'A' && s[x] == 'B' && s[x + 1] == 'C');if (x > 1) cnt += (s[x - 2] == 'A' && s[x - 1] == 'B' && s[x] == 'C');return cnt;};int res = 0;for (int i = 0; i < n - 2; i ++)if (s[i] == 'A' && s[i + 1] == 'B' && s[i + 2] == 'C') res ++, i += 2;while (q --) {int x;char c;cin >> x >> c, x --;res -= count(x), s[x] = c, res += count(x);cout << res << endl;}return 0;
}

D - Buildings

Problem Statement

There are $N$ buildings, Building $1$, Building $2$, $\dots$, Building $N$, arranged in a line in this order. The height of Building $i$ $(1\le i\le N)$ is $H_i$.
For each $i=1,2,\dots ,N$, find the number of integers $j$ KaTeX parse error: Expected 'EOF', got '&' at position 4: (i &̲lt; j \leq N) satisfying the following condition:
There is no building taller than Building $j$ between Buildings $i$ and $j$.

Constraints

$1\le N\le 2\times 10^5$
$1\le H_i\le N$
$ H_i\neq H_j\ (i\neq j)$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$
$H_1$ $H_2$ $\ldots$ $H_N$

Output

For each $i=1,2,\dots ,N$, let $c_i$ be the number of $j$ satisfying the condition. Print $c_1,c_2,\dots ,c_N$ in order, separated by spaces.

Sample Input 1

5
2 1 4 3 5

Sample Output 1

3 2 2 1 0

For $i=1$, the integers $j$ satisfying the condition are $2$, $3$, and $5$: there are three. (Between Buildings $1$ and $4$, there is a building taller than Building $4$, which is Building $3$, so $j=4$ does not satisfy the condition.) Therefore, the first number in the output is $3$.

Sample Input 2

4
1 2 3 4

Sample Output 2

3 2 1 0

Sample Input 3

10
1 9 6 5 2 7 10 4 8 3

Sample Output 3

2 3 3 3 2 1 2 1 1 0

Solution

具体见文末视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;signed main() {cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int n;cin >> n;std::vector<int> a(n + 1);for (int i = 1; i <= n; i ++) cin >> a[i];stack<int> stk;std::vector<int> res(n + 1, 0);for (int i = n; i >= 1; i --) {res[i] = stk.size();while (stk.size() && stk.top() < a[i]) stk.pop();stk.push(a[i]);}for (int i = 1; i <= n; i ++) cout << res[i] << " ";cout << endl;return 0;
}

---

E - K-th Largest Connected Components

Problem Statement

There is an undirected graph with $N$ vertices and $0$ edges. The vertices are numbered $1$ to $N$.
You are given $Q$ queries to process in order. Each query is of one of the following two types:
Type $1$: Given in the format 1 u v. Add an edge between vertices $u$ and $v$.
Type $2$: Given in the format 2 v k. Print the $k$-th largest vertex number among the vertices connected to vertex $v$. If there are fewer than $k$ vertices connected to $v$, print -1.

Constraints

$1\le N,Q\le 2\times 10^5$
In a Type $1$ query, KaTeX parse error: Expected 'EOF', got '&' at position 10: 1 \leq u &̲lt; v \leq N.
In a Type $2$ query, $1\le v\le N$, $1\le k\le 10$.
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$ $Q$
${\mathrm{query}}_1$
${\mathrm{query}}_2$
$⋮$
${\mathrm{query}}_Q$

Here, ${\mathrm{query}}_i$ is the $i$-th query and is given in one of the following formats:

$1$ $u$ $v$

$2$ $v$ $k$

Output

Let $q$ be the number of Type $2$ queries. Print $q$ lines.
The $i$-th line should contain the answer to the $i$-th Type $2$ query.

Sample Input 1

4 10
1 1 2
2 1 1
2 1 2
2 1 3
1 1 3
1 2 3
1 3 4
2 1 1
2 1 3
2 1 5

Sample Output 1

2
1
-1
4
2
-1

In the first query, an edge is added between vertices $1$ and $2$.
In the second query, two vertices are connected to vertex $1$: $1$ and $2$. Among them, the $1$-st largest vertex number is $2$, which should be printed.
In the third query, two vertices are connected to vertex $1$: $1$ and $2$. Among them, the $2$-nd largest vertex number is $1$, which should be printed.
In the fourth query, two vertices are connected to vertex $1$: $1$ and $2$, which is fewer than $3$, so print -1.
In the fifth query, an edge is added between vertices $1$ and $3$.
In the sixth query, an edge is added between vertices $2$ and $3$.
In the seventh query, an edge is added between vertices $3$ and $4$.
In the eighth query, four vertices are connected to vertex $1$: $1,2,3,4$. Among them, the $1$-st largest vertex number is $4$, which should be printed.
In the ninth query, four vertices are connected to vertex $1$: $1,2,3,4$. Among them, the $3$-rd largest vertex number is $2$, which should be printed.
In the tenth query, four vertices are connected to vertex $1$: $1,2,3,4$, which is fewer than $5$, so print -1.

Sample Input 2

6 20
1 3 4
1 3 5
2 1 1
2 3 1
1 1 5
2 6 9
2 1 3
2 6 1
1 4 6
2 2 1
2 6 2
2 4 7
1 1 4
2 6 2
2 3 4
1 2 5
2 4 1
1 1 6
2 3 3
2 1 3

Sample Output 2

1
5
-1
3
6
2
5
-1
5
3
6
4
4

Solution

具体见文末视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;signed main() {cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int n, q;cin >> n >> q;std::vector<set<int>> pnt(n + 1);std::vector<int> par(n + 1);for (int i = 1; i <= n; i ++) par[i] = i, pnt[i].insert(i);auto find = [&](auto self, int x) -> int {if (par[x] != x) par[x] = self(self, par[x]);return par[x];};while (q -- ) {int op, u, v;cin >> op >> u >> v;if (op == 1) {int pu = find(find, u), pv = find(find, v);if (pu == pv) continue;if (pnt[pu].size() > pnt[pv].size()) swap(pu, pv);for (auto v : pnt[pu]) pnt[pv].insert(v);par[pu] = pv;} else {if (pnt[find(find, u)].size() < v) cout << -1 << endl;else {auto it = pnt[find(find, u)].end();v --, it --;while (v -- ) it --;cout << *it << endl;}}}return 0;
}

---

F - Teleporting Takahashi 2

Problem Statement

There is a simple directed graph $G$ with $N$ vertices and $N+M$ edges. The vertices are numbered $1$ to $N$, and the edges are numbered $1$ to $N+M$.
Edge $i$ $(1\le i\le N)$ goes from vertex $i$ to vertex $i+1$. (Here, vertex $N+1$ is considered as vertex $1$.)

Edge $N+i$ $(1\le i\le M)$ goes from vertex $X_i$ to vertex $Y_i$.
Takahashi is at vertex $1$. At each vertex, he can move to any vertex to which there is an outgoing edge from the current vertex.
Compute the number of ways he can move exactly $K$ times.
That is, find the number of integer sequences $(v_0,v_1,\dots ,v_K)$ of length $K+1$ satisfying all of the following three conditions:
$1\le v_i\le N$ for $i=0,1,\dots ,K$.
$v_0=1$.
There is a directed edge from vertex $v_{i-1}$ to vertex $v_i$ for $i=1,2,\dots ,K$.
Since this number can be very large, print it modulo $998244353$.

Constraints

$2\le N\le 2\times 10^5$
$0\le M\le 50$
$1\le K\le 2\times 10^5$
$1\le X_i,Y_i\le N$, $X_i\ne Y_i$
All of the $N+M$ directed edges are distinct.
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$ $M$ $K$
$X_1$ $Y_1$
$X_2$ $Y_2$
$⋮$
$X_M$ $Y_M$

Output

Print the count modulo $998244353$.

Sample Input 1

6 2 5
1 4
2 5

Sample Output 1

5

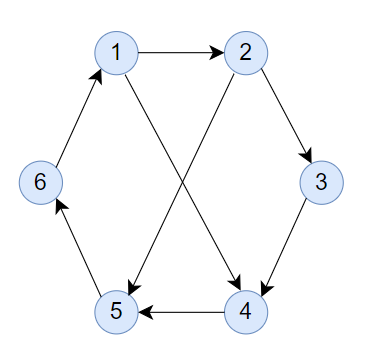The above figure represents the graph $G$. There are five ways for Takahashi to move: Vertex $1 \to$ Vertex $2 \to$ Vertex $3 \to$ Vertex $4 \to$ Vertex $5 \to$ Vertex $6$ Vertex $1 \to$ Vertex $2 \to$ Vertex $5 \to$ Vertex $6 \to$ Vertex $1 \to$ Vertex $2$ Vertex $1 \to$ Vertex $2 \to$ Vertex $5 \to$ Vertex $6 \to$ Vertex $1 \to$ Vertex $4$ Vertex $1 \to$ Vertex $4 \to$ Vertex $5 \to$ Vertex $6 \to$ Vertex $1 \to$ Vertex $2$ Vertex $1 \to$ Vertex $4 \to$ Vertex $5 \to$ Vertex $6 \to$ Vertex $1 \to$ Vertex $4$ #### Sample Input 2 ``` 10 0 200000 ``` #### Sample Output 2 ``` 1 ``` #### Sample Input 3 ``` 199 10 1326 122 39 142 49 164 119 197 127 188 145 69 80 6 120 24 160 18 154 185 27 ``` #### Sample Output 3 ``` 451022766 ```

Solution

具体见文末视频。

---

Code

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int N = 2e5 + 10, M = 1e2 + 10, mod = 998244353;int n, m, k;
std::vector<PII> g[N];
int st[N], dp[M][N], pnt[M], to[M];signed main() {cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> n >> m >> k;while (m -- ) {int u, v;cin >> u >> v;g[u].emplace_back(v, 1), st[u] = st[v] = 1;}int lst = 1, cnt = 0;unordered_map<int, int> idx;idx[1] = ++ cnt, pnt[1] = 1;for (int i = 2; i <= n; i ++)if (st[i]) {g[lst].emplace_back(i, i - lst), to[cnt] = i - lst;lst = i, idx[i] = ++ cnt, pnt[cnt] = i;}if (~lst) g[lst].emplace_back(1, n - lst + 1), to[cnt] = n - lst + 1;dp[idx[1]][0] = 1;for (int j = 0; j <= k; j ++)for (int i = 1; i <= cnt; i ++) {int u = pnt[i];for (auto v : g[u])if (j + v.se <= k)(dp[idx[v.fi]][j + v.se] += dp[i][j]) %= mod;}int res = 0;for (int i = 1; i <= cnt; i ++) {// int lst = i - 1;// if (!lst) lst = cnt;// cout << to[lst] << endl;for (int j = k - to[i] + 1; j <= k; j ++) {(res += dp[i][j]) %= mod;// cout << i << " " << j << ":" << dp[i][j] << endl;}}cout << res << endl;return 0;
}

---

视频题解

---

最后祝大家早日