一、经验总结
子序列 VS 子数组
- 子数组要求:顺序,连续,数量级n^2
- 子序列要求:顺序,任意选取(可以连续也可以不连续),数量级2^n(更大)
- 也就是说子数组是子序列的子集
由于子序列不连续的特点,在以i位置为结尾的子序列包括:
- 长度为1:i位置的元素自成一个单元素子序列
- 长度大于1:以i位置结尾的多元素子序列,需要遍历i位置之前的所有位置j作为作为子序列的前驱
对于复杂序列的子序列问题,如:斐波那契数列,等差数列。
- 传统的以i位置为结尾的状态表示,推导不出状态转移方程。因为单一位置不能确定一个斐波那契数列。至少需要最后两项才能确定一个斐波那契数列。因此需要创建一个二维dp表,用两个位置[i, j]确定一个状态。
- 可以使用哈希表优化算法:将数组中的所有元素与他们的下标绑定,保存在哈希表中。在用[i, j]位置求出等差数列的倒数第3项时,可以利用哈希表快速得到该元素的下标。
- 详细解释见例题:2.6,2.7,2.8。
二、相关编程题解析
2.1 最长递增子序列
题目链接
300. 最长递增子序列 - 力扣(LeetCode)
题目描述

算法原理

编写代码
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n, 1);int ret = 1;for(int i = 1; i < n; ++i){for(int j = 0; j < i; ++j){if(nums[i] > nums[j])dp[i] = max(dp[i], dp[j]+1);}ret = max(ret, dp[i]);}return ret;}
};
2.2 摆动序列
题目链接
376. 摆动序列 - 力扣(LeetCode)
题目描述

算法原理

对比【动态规划】子数组系列中的最长湍流子数组,在最长湍流子数组中可以使用单状态(单个dp表)解题。就是因为子数组连续的特点,可以确定i, i-1, i-2位置的值,用于判断子数组数据最后两段的单调性是否相异。
但是这道摆动序列是子序列问题,序列顺序但不连续,因此不能确定j位置之前数据的值。需要使用两种状态(2个dp表)一种用于记录最后一个位置是递增序列,另一种用于记录最后一个位置是递减序列。
编写代码
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();vector<int> f(n, 1), g(n, 1);int ret = 1;for(int i = 1; i < n; ++i){for(int j = 0; j < i; ++j){if(nums[j] < nums[i])f[i] = max(f[i], g[j]+1);else if(nums[j] > nums[i])g[i] = max(g[i], f[j]+1);}ret = max(ret, max(f[i], g[i]));}return ret;}
};
2.3 最长递增子序列的个数
题目链接
673. 最长递增子序列的个数 - 力扣(LeetCode)
题目描述

算法原理

编写代码
class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> len(n, 1), count(n, 1);int maxlen = 1, ret = 1;for(int i = 1; i < n; ++i){//找出以i位置为结尾的最长递增子序列的长度len[i]和个数count[i]for(int j = 0; j < i; ++j){if(nums[j] < nums[i]){if(len[j]+1 == len[i])count[i]+=count[j];if(len[j]+1 > len[i]){len[i] = len[j]+1;count[i] = count[j];}}}//找出所有位置中的最长递增子序列的长度maxlen和个数retif(len[i] == maxlen) ret+=count[i];else if(len[i] > maxlen) maxlen=len[i], ret=count[i];}return ret;}
};
2.4 最长数对链
题目链接
646. 最长数对链 - 力扣(LeetCode)
题目描述

算法原理
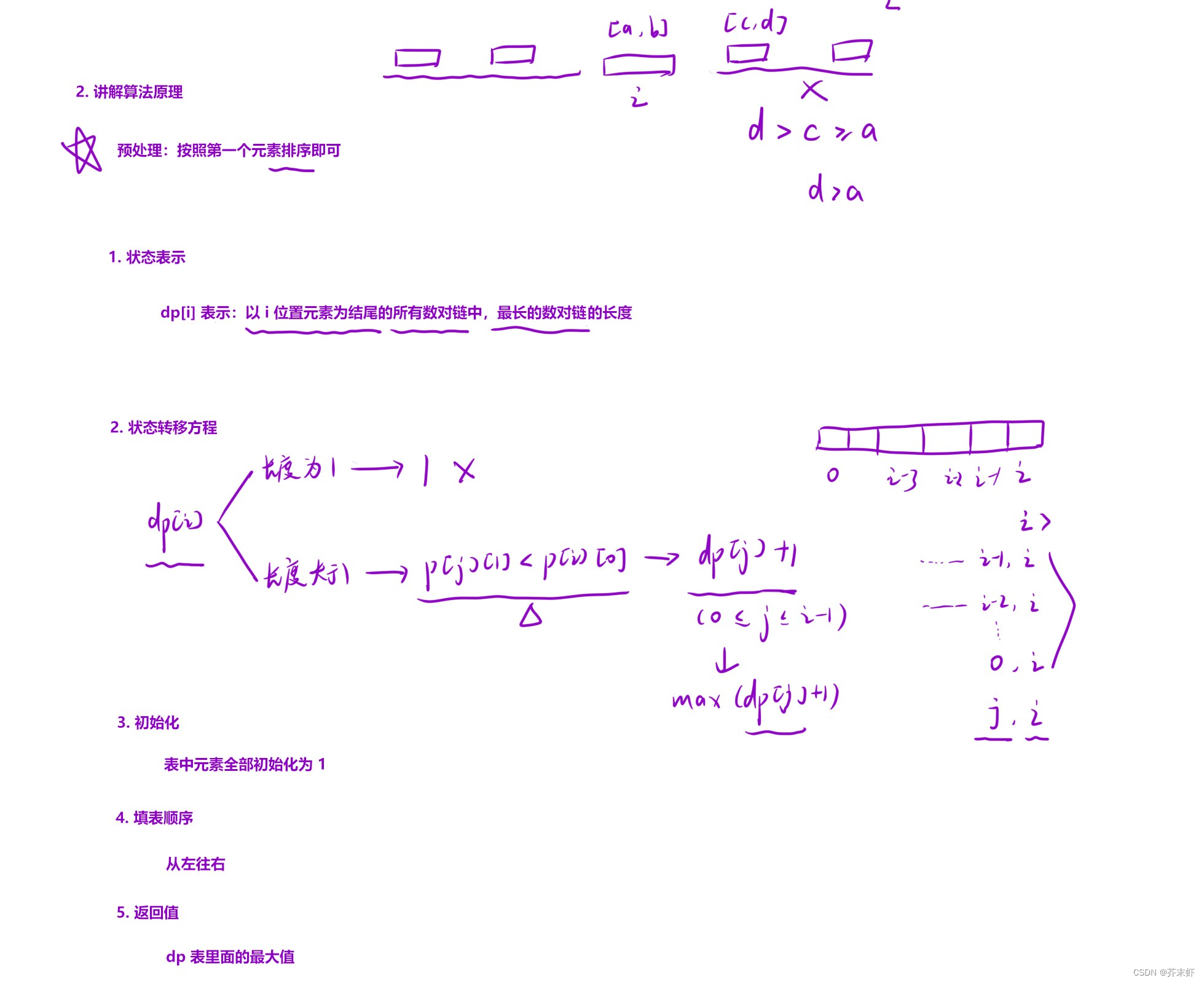
编写代码
class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) {sort(pairs.begin(), pairs.end());int n = pairs.size();vector<int> dp(n, 1);int ret = 1;for(int i = 1; i < n; ++i){for(int j = 0; j < i; ++j){if(pairs[j][1] < pairs[i][0]){dp[i] = max(dp[i], dp[j]+1);}}ret = max(ret, dp[i]);}return ret;}
};
2.5 最长定差子序列
题目链接
1218. 最长定差子序列 - 力扣(LeetCode)
题目描述

算法原理

为什么这道题可以使用哈希表进行优化呢?
-
因为相同大小的值在数组中的位置越靠后对应子序列的长度就可能越大,因此我们可以直接选择最后一次出现的b(a-diff)值的dp值,而哈希表在从左往右遍历的过程中刚好就是将最后一次出现的数值的dp值更新为哈希值。
-
通过哈希表的优化,免去了第二层的遍历(寻找子序列中当前节点的前驱)。
编写代码
class Solution {
public:int longestSubsequence(vector<int>& arr, int diff) {unordered_map<int, int> hash; //<arr[i], dp[i]>hash[arr[0]] = 1;int ret = 1;for(int i = 1; i < arr.size(); ++i){hash[arr[i]] = hash[arr[i]-diff]+1;ret = max(ret, hash[arr[i]]);}return ret;}
};
//解释:
//1. 如果arr[i]-diff不存在,所对应的哈希值就是0,0+1刚好就是结果。
//2. 因为从左往右的遍历顺序,hash[arr[i]-diff]能够保证存放的是遍历过程中出现的最后一个arr[i]-diff的dp值,既然是最后一个一定是最大值
2.6 最长的斐波那契子序列的长度
题目链接
873. 最长的斐波那契子序列的长度 - 力扣(LeetCode)
题目描述

算法原理
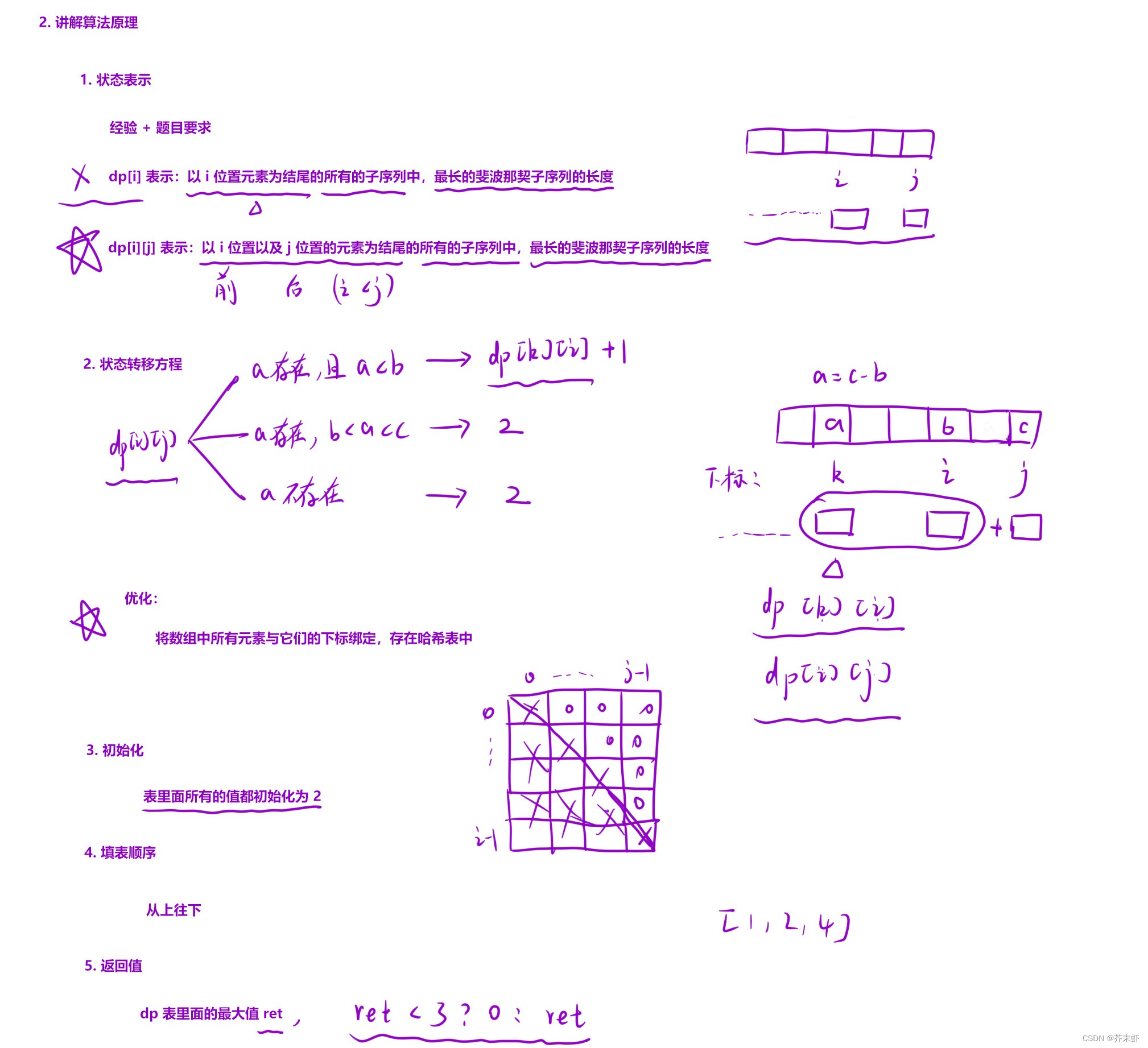
-
根据第一个状态表示推到不出状态转移方程,证明该状态表示是错误的,需要重新设计状态表示。
-
由于这是道子序列问题,所以单一位置不能确定一个斐波那契数列。至少需要最后两项才能确定一个斐波那契数列。因此就有了第二个状态表示
编写代码
class Solution {
public:int lenLongestFibSubseq(vector<int>& arr) {unordered_map<int, int> hash;int n = arr.size();for(int i = 0; i < n; ++i)hash[arr[i]] = i;vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for(int j = 2; j < n; ++j){for(int i = 1; i < n; ++i){int a = arr[j]-arr[i];if(a < arr[i] && hash.count(a))dp[i][j] = dp[hash[a]][i]+1;ret = max(ret, dp[i][j]);}}return ret<3? 0:ret;}
};
2.7 最长等差数列
题目链接
1027. 最长等差数列 - 力扣(LeetCode)
题目描述

算法原理

-
根据第一个状态表示推到不出状态转移方程,证明该状态表示是错误的,需要重新设计状态表示。
-
由于这是道子序列问题,所以单一位置不能确定一个等差序列。至少需要等差序列的最后两项才能确定一个等差序列。因此就有了第二个状态表示
-
为什么要一边dp,一边保存<元素,下标>到哈希表?
- 由于哈希表中元素的下标一直紧跟i,可以直接排除 “a存在,但i<k<j“ 的情况
- 同时保证了哈希表中保存的是离i最近的元素的下标
注意:上一题不需要这样,是因为题目条件给定的是一个严格递增的正整数数组
-
为了保证可以一边dp,一边填哈希表,填表策略也要做出相应的调整:应该固定倒数第二个数 i,枚举最后一个数 j,这样才能正确的、不重复的填写紧跟在i之后的元素的下标到哈希表。
编写代码
class Solution {
public:int longestArithSeqLength(vector<int>& nums) {int n = nums.size();unordered_map<int, int> hash;hash[nums[0]] = 0;vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for(int i = 1; i < n; ++i) //先固定倒数第二个数i{for(int j = i+1; j < n; ++j) //枚举倒数第一个数j{int a = 2*nums[i]-nums[j];if(hash.count(a)){dp[i][j] = dp[hash[a]][i]+1;}ret = max(ret, dp[i][j]);}hash[nums[i]] = i; //一边dp,一边填写哈希表}return ret;}
};
2.8 等差序列划分Ⅱ
题目链接
446. 等差数列划分 II - 子序列 - 力扣(LeetCode)
题目描述

算法原理

-
上一题统计的是最长等差数列的长度,将<元素,下标>绑定在一起,保存的是离i最近的元素的下标。
-
本题要统计所有等差序列的个数,所以要将<元素,下标数组>绑定在一起,方便找到该元素出现过的所有位置。
编写代码
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();vector<vector<int>> dp(n, vector<int>(n));unordered_map<long long, vector<int>> hash;for(int i = 0; i < n; ++i)hash[nums[i]].push_back(i);int ret = 0;for(int j = 2; j < n; ++j){for(int i = 1; i < j; ++i){long long a = (long long)2*nums[i]-nums[j];if(hash.count(a)){for(auto k : hash[a])if(k < i) dp[i][j] += dp[k][i]+1;}ret+=dp[i][j];}}return ret;}
};














