📝前言说明:
- 本专栏主要记录本人的基础算法学习以及LeetCode刷题记录,按专题划分
- 每题主要记录:(1)本人解法 + 本人屎山代码;(2)优质解法 + 优质代码;(3)精益求精,更好的解法和独特的思想(如果有的话)
- 文章中的理解仅为个人理解。如有错误,感谢纠错
🎬个人简介:努力学习ing
📋本专栏:C++刷题专栏
📋其他专栏:C语言入门基础,python入门基础,C++学习笔记,Linux
🎀CSDN主页 愚润泽
视频
- 202. 快乐数
- 个人解
- 优质解:
- 11 盛最多水的容器
- 个人解
- 优质解:
- 611. 有效三角形的个数
- 个人解
- 优质解:
202. 快乐数

个人解
思路:没思路,不知道如何判断这个数不是快乐树
用时:13:00
屎山代码:无
优质解:
思路:不要偷懒,自己手算一遍这个过程才能发现规律

你要问我为什么一定能成环?
题目所给的数字范围:1 <= n <= 2^31 - 1,2^31 - 1 == 2,147,483,647,总共有9位数,我们往大了取,假设每一位都为9,则999999999的平方和肯定是最大的,结果是9*9*10 == 810,那最小的数呢?显然是1,也就是说每次变化的取值是在[1, 810]里面取。
但是,无限循环,取无数次,在[1, 810]里面取无数次,必然有重复!
对于能变成1的快乐数,因为1的平方还是1,所以,最后也是在一个全是1的环内循环
所以,这道题就变成:可以用快慢指针,慢指针每次移动一步,快指针每次移动两步,因为有速度差且有环,所以快慢指针一定会在环内相遇。当快慢指针相遇时,判断相遇的数是否为1即可。
代码:
class Solution {
public:int Sum(int n){int sum = 0;while(n){int i = n % 10;sum += i * i;n /= 10;}return sum;}bool isHappy(int n) {int slow = n, fast = Sum(n); // 这里可不能 fast == n, 因为while的判断条件是slow == fastwhile(slow != fast){slow = Sum(slow);fast = Sum(Sum(fast));}return slow == 1;}
};
11 盛最多水的容器

个人解
思路:
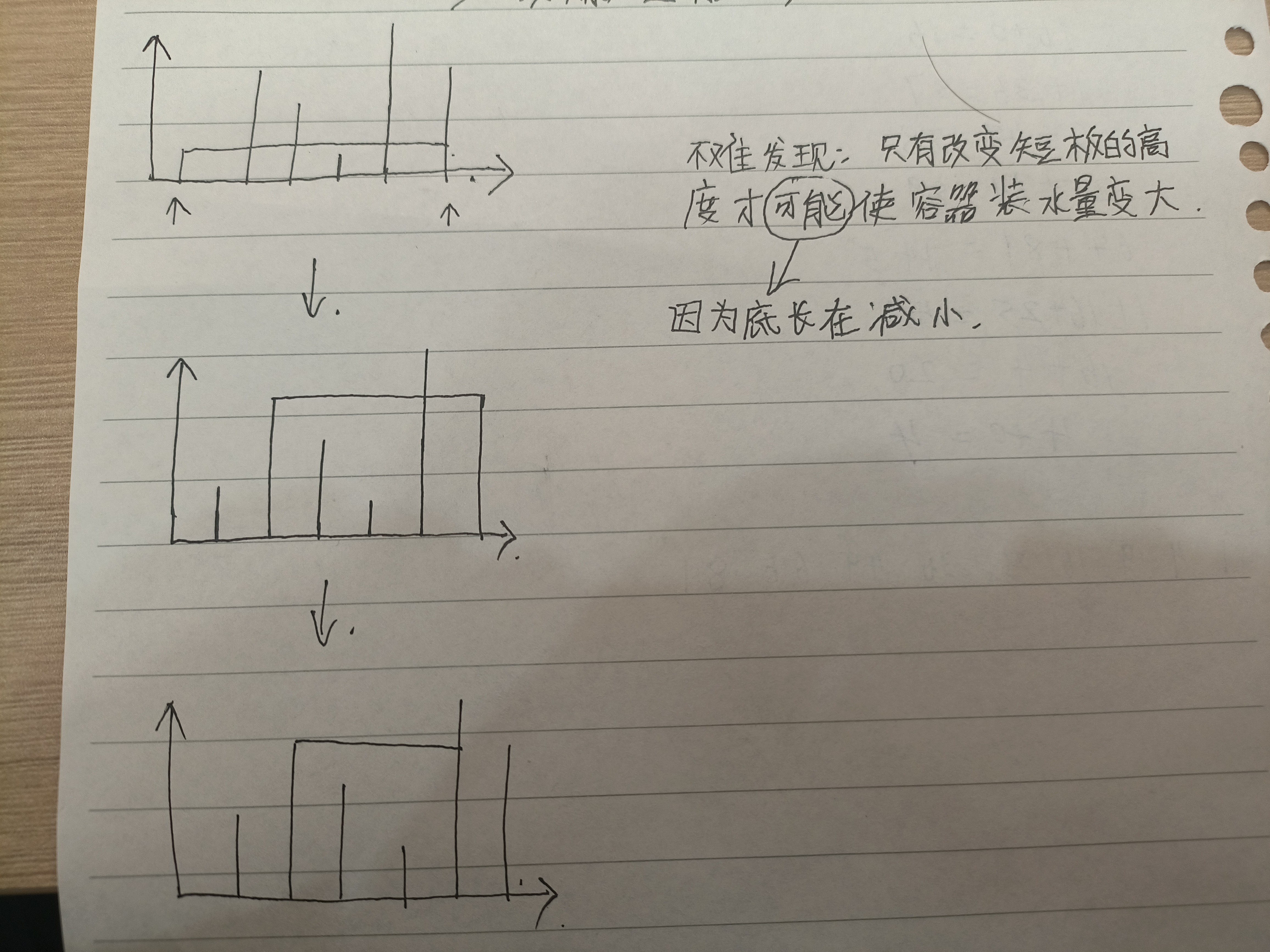
每次让短的边移动。
移动完成后,重新计算容积V的大小,如果更大就替换
用时:10:00(通过,因为这题以前写过)
屎山代码:
class Solution {
public:int maxArea(vector<int>& height) {int ans = 0, left = 0, right = height.size() - 1;while(left < right){int v = min(height[left], height[right]) * (right - left);if(v > ans) ans = v;else{if(height[left] < height[right]){left++;}else{right--;}}}return ans;}
};
时间复杂度:O(n)
空间复杂度:O(1)
优质解:
个人解已经比较优秀的解法了,不再过多探索
611. 有效三角形的个数

个人解
思路:通过枚举 最大边 + 相向指针 求解。
- 先对数组进行排序,整个数组递增
- 枚举最大边
cur,然后设置双指针:right = cur - 1,left = 0 - 要满足可以形成三角形,就需要两个短边之和 > 最大边
- 又因为数组有递增性,如果当前的
left,right,cur所指向的三个数可以形成三角形,则right和left到right之间的所有数组合也可以形成三角形,因为这些值>=left指向的值。 - 双指针的移动问题,要满足
nums[left] + nums[right] > nums[cur],很明显:left左移,会让左式更大,right右移会让左式更小。所以当不满足条件的时候,left左移,当满足条件以后right右移。
但是,我在做题的时候一开始尝试 枚举最小边 + 相向指针 出现了问题:如果我枚举的是最小边,则要满足:nums[right] - nums[left] < nums[cur],这时候因为数组是递增的,就出现了问题。因为right左移,左式会变小,left右移左式也会变小,变化相同显然是行不通的。
用时:18:00
屎山代码(通过):
class Solution {
public:int triangleNumber(vector<int>& nums) {int ans = 0, n = nums.size();ranges::sort(nums); // ranges 是 C++20 引入的ranges库for(int cur = n - 1; cur > 1; cur--) // 枚举最长边{int left = 0, right = cur - 1;while(left < right){if(nums[left] + nums[right] > nums[cur]){ans += right - left;right--;}else{left++;}}}return ans;}
};
时间复杂度:O( n 2 n^2 n2)
空间复杂度:O(1)
优质解:
枚举最小边的处理方法:
用同向双指针(滑动窗口)。
当left和right的指针越靠近的时候,两边的差值越小。
我们可以,一开始让right和left足够接近,让[left, right]这个窗口里面的组合都满足nums[right] - nums[left] < nums[cur],即:可以构成三角形
如何实现呢?
只需要在满足nums[right] - nums[left] < nums[cur]的时候,让left右移,移动到第一个满足的地方就停下来,然后统计窗口内满足的个数,加入ans。一组算完以后,让right右移变远,但是left无须倒退,因为right增大了,左式增大,这时候要找的是让左式更小的left(这个很关键,不然容易写成O( n 3 n^3 n3),我就是,进行了回退…),进行下一组的计算。
代码:
class Solution {
public:int triangleNumber(vector<int>& nums) {int ans = 0, n = nums.size();ranges::sort(nums); // ranges 是 C++20 引入的ranges库for(int cur = 0 ; cur < n - 2; cur++) // 枚举最短边{int left = cur + 1;for(int right = cur + 2; right < n; right++){while(left < right && nums[right] - nums[left] >= nums[cur]){left++;}ans += right - left;}}return ans;}
};
时间复杂度:O( n 2 n^2 n2)
空间复杂度:O(1)
🌈我的分享也就到此结束啦🌈
要是我的分享也能对你的学习起到帮助,那简直是太酷啦!
若有不足,还请大家多多指正,我们一起学习交流!
📢公主,王子:点赞👍→收藏⭐→关注🔍
感谢大家的观看和支持!祝大家都能得偿所愿,天天开心!!!














