本文图片和部分材料来源网络,如有侵权,请联系我删除,谢谢!
一.贪心
现在我们来学习贪心:
1.贪心是什么?
贪心算法(Greedy Algorithm)是一种基于贪心思想的算法策略。它通过每一步选择当前状态下最优的解决方案,从而逐步得到全局最优解
贪心算法的步骤:
1、确定问题的最优子结构
2、定义(每一步)贪心选择策略
3、构建方案及验证方案
那么,我们先讲一道例题吧!
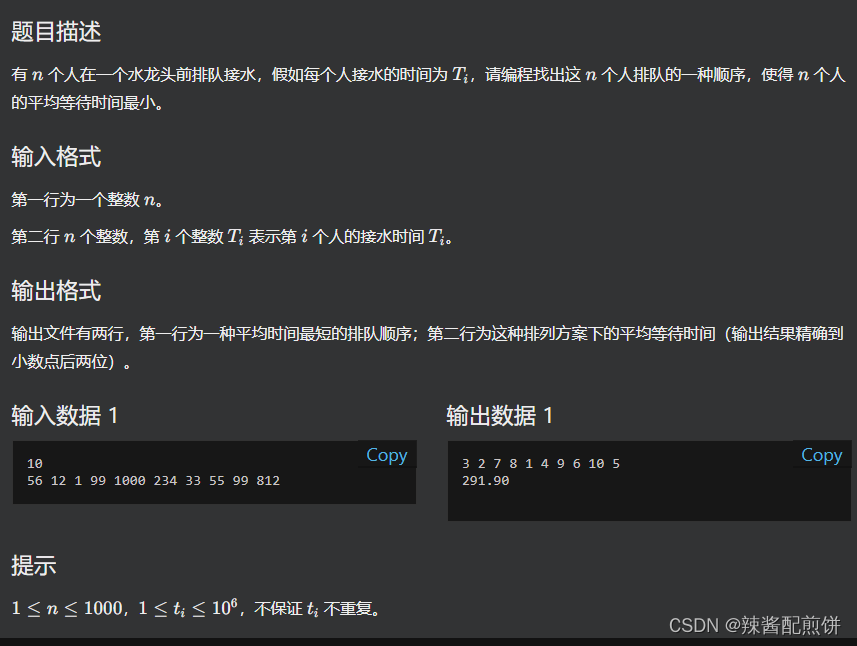
看完题目,你觉得它的贪心策略是什么?
这里做一个投票(在最下面,题目为 “ 单项选择题(1)贪心策略是什么?” )
好了这里的正确答案是A
因为节水总时长要少,那么就要先让接水时间少的先接水(注意,这里说了t[i]可能会重复)
这里我们需要用到结构体,所以需要写一个排序规则的函数(函数文章指路):
struct w{int id,b;
}a[1005];
bool cmp(w x,w y)
{if(y.b==x.b){return x.id<y.id;}return x.b<y.b;
}那么接下来,我们 来写输入输出以及排序:
int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i].b;a[i].id=i;}sort(a+1,a+1+n,cmp);这里有一个坑,末尾不能输出空格(好雷),错了不知道多少次
(我用的方法是:先输出第一个,然后输出空格,再输出其他的)
输出部分:
cout<<a[1].id;double s=a[1].b;for(int i=2;i<=n;i++){cout<<" "<<a[i].id;sum+=s;s+=a[i].b;}cout<<endl;printf("%.2lf",sum/n);完整代码:
#include<bits/stdc++.h>
using namespace std;
double sum=0.0;
struct w{int id,b;
}a[1005];
bool cmp(w x,w y)
{if(y.b==x.b){return x.id<y.id;}return x.b<y.b;
}
int main()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i].b;a[i].id=i;}sort(a+1,a+1+n,cmp);cout<<a[1].id;double s=a[1].b;for(int i=2;i<=n;i++){cout<<" "<<a[i].id;sum+=s;s+=a[i].b;}cout<<endl;printf("%.2lf",sum/n);return 0;
}那么,简单的贪心,你学会了嘛?
留一道习题:
二.动态规划
我们知道,动态规划有很多类型
现在我们来讲解——最长上升子序列!
动态规划简称 DP/dp(dynamic programming)
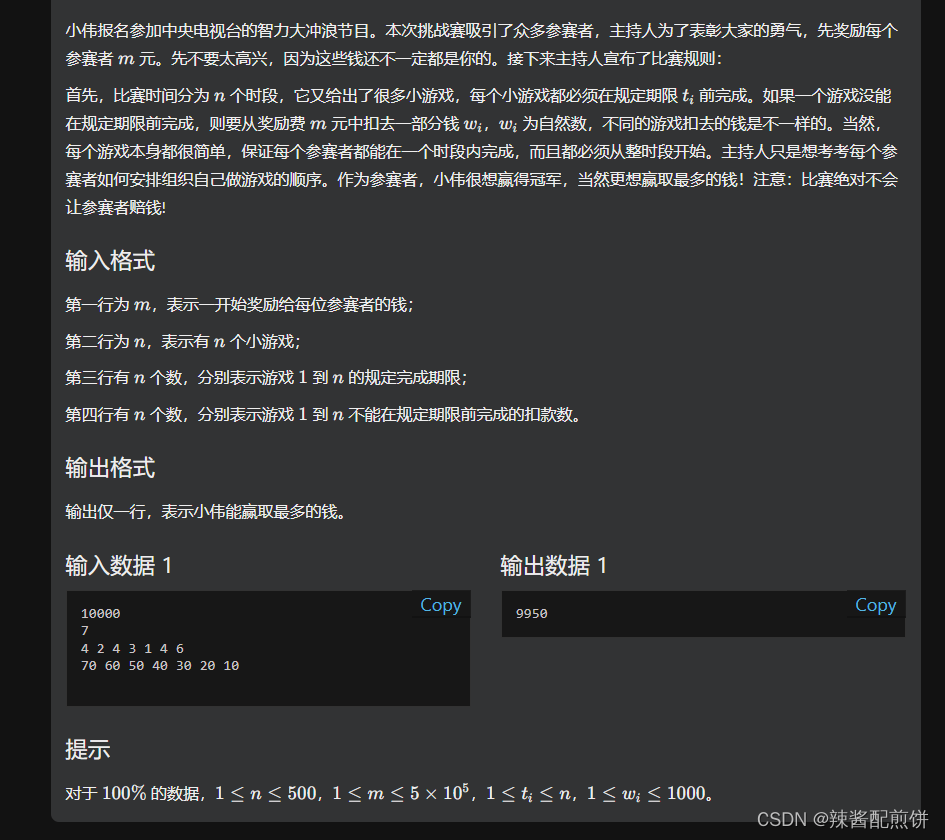
题目
 在学习动态规划之前,我们要先学会几个步骤:
在学习动态规划之前,我们要先学会几个步骤:
1.把一个大问题拆分成多个小问题
2.推导状态转移方程
3. 考虑边界问题
那么,这道题的状态转移方程是什么呢?
(如果前面任意一个数比现在我们搜索的数小,并且是比我们现在搜索的数小里面,下方数值最多的,那么这个数下方的数值=下方数值最多的)
| 13 | 7 | 9 | 16 | 38 | 24 | 37 | 18 | 44 | 19 | 21 | 22 | 63 | 15 | |
| 无 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 4 | 6 | 6 | 7 | 8 | 7 | 3 |
不难发现,状态转移方程是:
dp[i]=max(dp[i],dp[j]+1);(注:如果用我的思路的话,在第一层循环结束时还要判一次最大值!)
代码:
#include<bits/stdc++.h>
using namespace std;
int main()
{int n,a[1005],dp[1005],mxx=0;cin>>n;dp[1]=1;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){dp[i]=1;for(int j=1;j<i;j++){if(a[i]>a[j]){dp[i]=max(dp[i],dp[j]+1);}}mxx=max(dp[i],mxx);}cout<<mxx;return 0;
}










)


