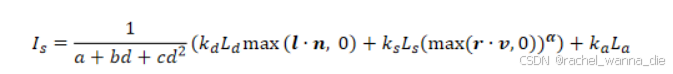计算机图形学期末复习
1. 基本几何要素
-
点(P,Q...):三维空间的一个位置
-
标量(α,β...):确定数量、长度,本身没有几何属性
-
向量(u,v...):方向+长度,没有位置信息
2. 标量-向量运算
-
逆向量:长度相同,方向相反(每个向量都有)
-
向量数乘:每个向量都能与标量相乘(零向量,零长度,方向不定)
-
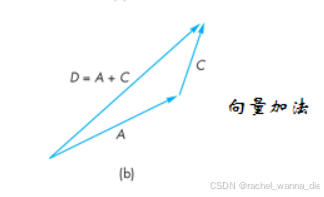
向量加法:三角形法则
3. 向量空间
def:线性空间,处理向量的数学系统(向量+标量)
-
运算:标量-向量乘法 向量-向量加法
向量空间不一定要有度量
-
度量:一种距离函数,衡量向量空间中任意两个向量之间的距离
4. 点积与叉积
-
点积(内积):u⋅v = |u| |v| cosθ【最后结果是标量】
-
叉积(外积):n = u × v =|u||v|sinθ【最后结果是向量,方向取决于向量前后,使用右手定则,四个手指从向量 u 转向向量 v,大拇指指向的方向为叉积得到的向量的方向】
-
点与向量之间运算:(1)点点相减得一个向量(2)点与向量相加得新点
-
向量:v = α1v1+ α2v2 +…+ αnvn
-
(向量加法)
-
αn为系数,vn为向量
-
v = [α1, α2 ,…,αn]T
-
齐次坐标:v = [α1, α2 ,…,αn,0]T
-
-
点:P =P_0+ β1v1+ β2v2 +…+ βnvn
-
(p_0指的原点,后面加多个向量)
-
βn为系数,vn为向量
-
P = [β1, β2 ,…, βn]T
-
齐次坐标:P = [β1, β2 ,…,β_n,1]T
-
5. 矩阵计算


6. 齐次坐标
-
三维空间的四维齐次坐标的一般形式为P = [x, y, z, w]T
-
w=0: 向量;w=1: 点
-
旋转
-
按z轴旋转(x,y轴类似)
-
x = r·cosϕ;y = r sinϕ
-
x' = r cos(ϕ+θ)=r(cosϕcosθ-sinϕsinθ)=xcosθ-ysinθ
-
y' = r sin(ϕ+θ)=r(sinϕcosθ+cosϕsinθ)=xsinθ+ycosθ
-
z' = z
-
旋转矩阵:

-
格式:旋转矩阵 × 点/向量矩阵
-
-
-
平移(只有点有平移,向量没有位置)
-
移动向量(a,b,c)
-
x'=x+a;y'=y+b;z'=z+c
-
点:

-
格式:移动矩阵×点矩阵
-
-
-
缩放
-
缩放因子(a,b,c)
-
x'=ax;y'=by;z'=cz
-
缩放矩阵:

-
格式:缩放矩阵×点/向量矩阵
-
-
7.视角坐标
-
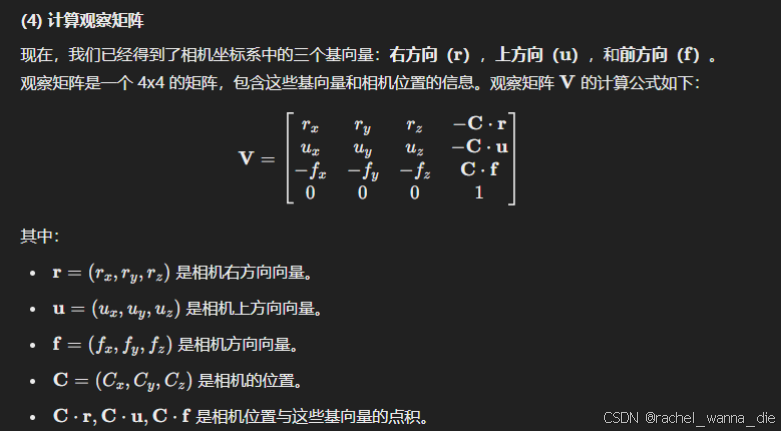
以摄像机的视角作为场景原点时场景中所有的顶点坐标:观察矩阵把所有的世界坐标变换为相对于摄像机位置与方向的观察坐标。要定义一个摄像机,我们需要它在世界空间中的位置、观察的方向、一个指向它右侧的向量以及一个指向它上方的向量。

- 其中up只是一个参考向量,相机上轴不一定与其相等
-
LookAt观察矩阵:
-
GLM已经提供了这些支持。我们要做的只是定义一个摄像机位置,一个目标位置和一个表示世界空间中的上向量的向量(我们计算右向量使用的那个上向量)。接着GLM就会创建一个LookAt矩阵,我们可以把它当作我们的观察矩阵:

-
-
正交投影
-
def:平行投影,投影不会因为远近发生变化(CAD)
-
无透视效果,平行
-
可以通过w = 0保证向量,w = 1保证点;
-
正交投影矩阵:
-
左右边界(x轴方向上)L,R
-
下上边界(y轴方向上)B,T
-
近远边界(z轴方向上)N,F
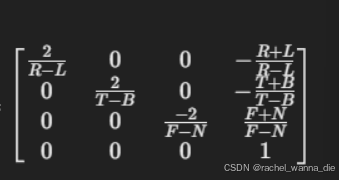
-
【好像】投影点位置 = 计算是观察矩阵×正交投影矩阵×点位置
-
齐次坐标
-
-
8. 光照与渲染
-
曲面上某一点的颜色取决于光照与材质之间的多次作用
-
相互作用(3)
-
镜面反射
-
一部分入射光线被吸收,反射出去的光纤沿着同一方向【入射角=反射角】
-
-
漫反射
-
向各个方向散射的光线强度相等
-
-
折射
-
允许入射光i西安的一部分进入表面,并从另一面发射出去
-
-
-
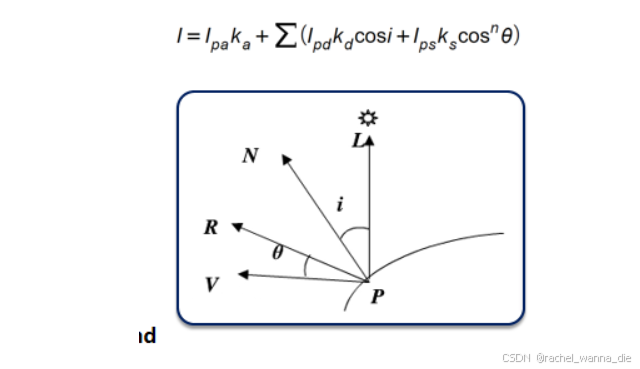
Phong光照反射模型(环境光+漫反射+镜面反射,分量的效果叠加)
-
环境光
-
环境光的量与颜色依赖于光源的颜色和对象的材料属性
-
在表面上所有点处的环境光强度I_a都是相同的
-
反射率由环境光反射系数k_a确定,即R_a=k_a
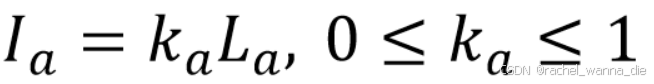
-
L_a可以代表任何单独的光源,也可以代表全局环境光
-
-
漫反射
-
光强公式:
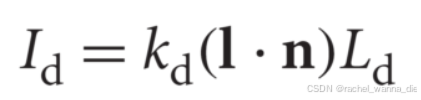
-
Id:物体表面的漫反射光强度
-
kd:物体表面的漫反射系数。
-
L:从光源到表面点的光线方向(单位向量)。
-
N:表面法线(单位向量)
-
N⋅L:法线和光源方向的点积,表示光源方向与表面法线的夹角。
-
Ld:光源的漫反射光强度
-
-
考虑传播过程中的衰减:
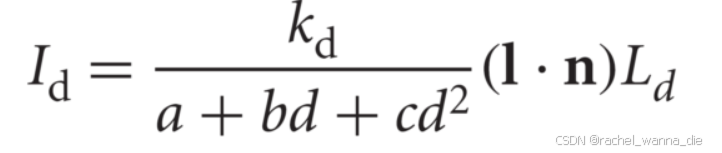
-
(chat说直接除以距离平方(?),但老师ppt上也没有细说abcd具体是什么)
-
-
镜面反射
-
光强公式:
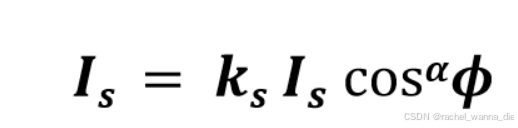
-
ϕ:视线与反射光线的夹角
-
α:高光系数,决定了反射光的衰减程度(镜面光滑度指数,决定了高光的锐利度)
-
ks:镜面反射系数
-
Is:光源的镜面反射光强度
-
-
改进phong模型
-
半程向量
-
def:半程向量是 光源方向向量和 视线方向向量的单位向量,它是两者的 单位向量和。
-
Ispecular=ks⋅Is⋅(N⋅H)n
-
半程向量和法线的夹角
-
-
-
冯氏光照模型(高洛德着色)-----有点逊色,不够真实【更高效】
-
光滑着色(高洛德着色)
-
在网格中每个顶点处有几个多边形交于该点,每个多边 形有一个法向,取这几个法向的平均得到该点的法向:
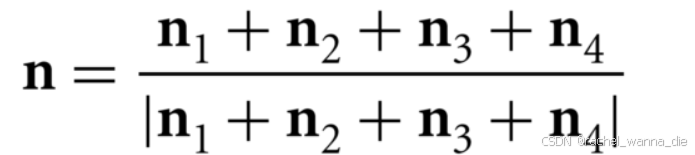
-
然后利用简单光照模型计算出顶点的颜色
-
对于多边形内的点,光栅化模块可以采用线性插值确定颜色
-
-
phong着色
-
根据每个顶点的法向,插值出多边形内部各点的法向,然后基于光照模型计算出各点的颜色:
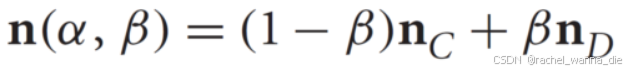
-
Phong着色在图形管线中通过片元着色器实现
-
9. 几何图元处理
-
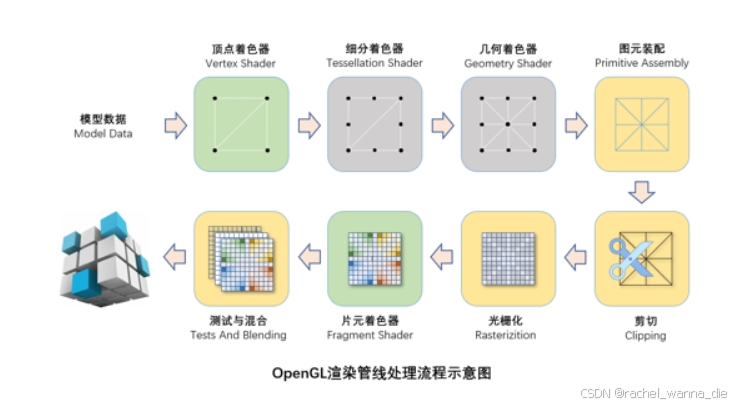
OpenGL渲染管线处理
-
数据模型->顶点着色器->细分着色器->集合着色器->图元装配->剪切->光栅化->片元着色器->测试与混合
-
裁剪
-
用来确定哪些图元的那些部分可能会出现在屏幕上,并且把没有被裁减掉的图元送入光栅化模块中
-
需要把在视见体外面的图元删除
-
Cohen-Sutherland算法【裁剪直线段的算法】效率不高
-
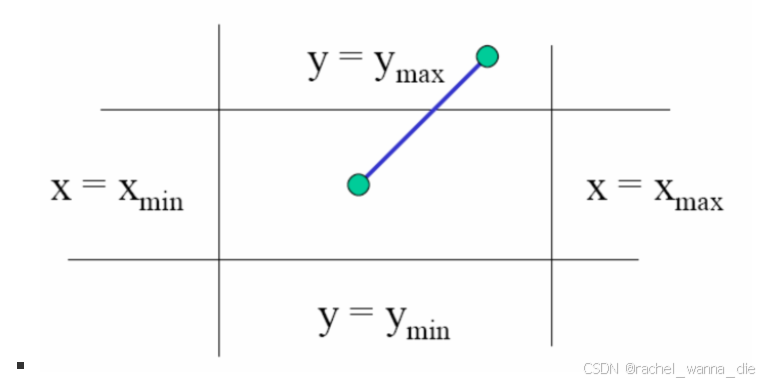
通过对端点编码的方式,尽可能不经过求交就消除许多情形从确定裁剪窗口边界的四条直线开始
-
对于每个端点定义一个编码b0b1b2b3【b0:y > ymax ;b1:y < ymin ; b2: x > xmax ; b3 : x < xmin】
-
-
Liang-Barsky裁剪算法【参数化,取消了分区编码】效率提升

-
确认视口的边界,对任意一条线段,判断是否与边界相交,计算交点。
-
-
光栅化【扫描转化】
-
把用一组顶点定义的对象内部的像素用相应的亮度激活。
-
将图元转换为实际的像素(片元)的过程。每个图元(如三角形)被拆解成多个片元,并计算每个片元的颜色、深度等信息。
-
算法:DDA、 Bresenham、 正负法、奇偶测试法、环绕测试法
DDA(数字微分分析器)
-
优点:
-
简单易懂:DDA算法的实现过程相对简单,易于理解和实现。
-
高效:相比于其他算法(如Bresenham算法),DDA算法执行过程较为直接,尤其在步长较小的情况下,计算速度较快。
-
-
缺点:
-
浮点运算:DDA算法需要进行浮点数计算,对于某些系统,浮点运算可能会影响性能,尤其是在低性能计算设备上。
-
精度问题:由于浮点计算会引入误差,在图形显示中可能会造成精度问题,导致直线稍微弯曲。
function DDA(x1, y1, x2, y2):dx = x2 - x1dy = y2 - y1steps = max(abs(dx), abs(dy)) Xinc = dx / steps Yinc = dy / steps x = x1 y = y1 for i from 1 to steps:plot(round(x), round(y)) // 绘制当前像素点x = x + Xincy = y + Yinc
-
-
-
Bresenham(布雷森汉姆)算法
-
DDA算法中每一步需要一次浮点加法
-
在Bresenham算法中可以不出现任何浮点运算
-
只考虑0 ≤ m ≤1的情形(m=dy/dx)
-
①判断直线的最大变化方向:首先计算出直线在X轴方向和Y轴方向各自变化量的绝对值,如果X轴方向变化量的绝对值更大则最大变化方向为X轴,反之最大变化方向为Y轴。 ②判断在最大变化方向上两个点的坐标是否满足升序排列,如果不满足,则交换两个点; ③分情况在两点之间进行下列循环过程:(设dx=x2-x1,dy=y2-y1)
-
For x = x1 to x2 doPlot point at (x, y)If (2(e' + Δy) < Δx)e' = e' + ΔyElsey = y + 1, e' = e' + Δy - ΔxEndIf EndFor
-
-
正负法
-
def:光栅化中一种常用的判断像素是否在三角形内部的方法
-
通过判断像素点与三角形某边的相对位置来确定是否在三角形内部。对于每个边,通过计算像素点到边的有符号距离,根据正负来判断像素点是否在边的一侧。如果所有的边都在其一侧,则像素点在三角形内部。反之,如果有一条边在像素点的另一侧,则像素点在三角形外部。
-
-
奇偶测试法(相交测试)
-
从一点p引射线,如果与多边形边界交点数为偶数,则p在多边形外,否则在多边形内部
-
如果交点为顶点,需要特别处理
-
-
-
-
环绕测试法
-
首先根据多边形的边界建立一条环路从一个顶点出发,依次遍历各边,最后回到该顶点
-
-