数据结构 --- 二叉树

一、满二叉树

在一棵二叉树中，如果所有分支节点都存在左子树和右子树，并且所有叶子节点都在同一层上，这

样的二叉树称为满二叉树。

每层节点数量为 2 ^ (n - 1)        （n为层数）

总节点个数为    2 ^ n - 1

二、完全二叉树

 在满二叉树的基础上，从上往下，从左往右增加节点；从下往上，从右往左减少节点

        满二叉树  ====  完全二叉树 

        完全二叉树  ====？ 满二叉树

三、二叉树的遍历

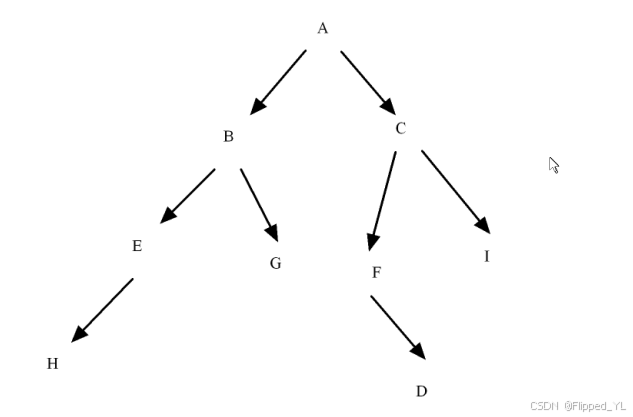
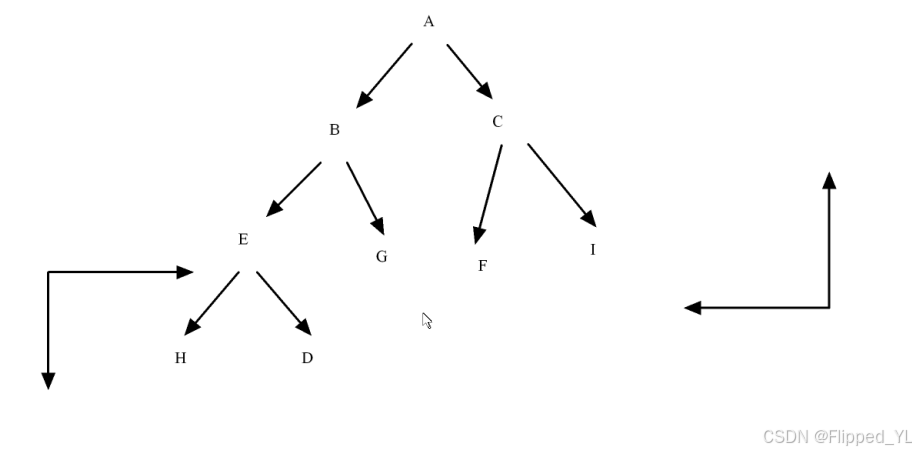
创建一个二叉树 （扩展二叉树）

pl(坐指针)

A

pr(右指针)

#ifndef __TREE_H__
#define __TREE_H__typedef char TDatatype;typedef struct tnode
{TDatatype data;struct tnode *pl;struct tnode *pr;
}tnode_t;tnode_t *create_bin_tree();
void pre_order(tnode_t *proot);
void mid_order(tnode_t *proot);
void behind_order(tnode_t *proot);
int get_tree_node(tnode_t *proot);
int get_tree_layer(tnode_t *proot);
void destroy_tree(tnode_t *proot);
void push_tree(tnode_t *proot);#endif

char tree[] = {"ABEH###G##CF#D##I##"};
int idx;tnode_t *create_bin_tree()
{TDatatype data = tree[idx++];if(data == '#'){return NULL;}tnode_t *pnode = (tnode_t *)malloc(sizeof(tnode_t));if(!pnode)return NULL;pnode->data = data;pnode->pl = create_bin_tree();pnode->pr = create_bin_tree();return pnode;
}

前序遍历：        根        左子树        右子树        ABEHGCFDI

中序遍历：        左子树        根        右子树        HEBGAFDCI

后序遍历：        左子树        右子树        根        HEGBDFICA

层序遍历：从上至下，从左至右，逐层遍历       ABCEGFIHD

已知        前序加中序 ------>还原二叉树

                后序加中序 ------>还原二叉树

四、代码实现 

 1、前序遍历

void pre_order(tnode_t *proot)
{if(NULL == proot)return;printf("%c ",proot->data);pre_order(proot->pl);pre_order(proot->pr);
}

2、中序遍历

void mid_order(tnode_t *proot)
{if(!proot)return ;mid_order(proot->pl);printf("%c ",proot->data);mid_order(proot->pr);
}

3、后序遍历

void behind_order(tnode_t *proot)
{if(!proot)return ;behind_order(proot->pl);behind_order(proot->pr);printf("%c ",proot->data);
}

4、层序遍历

层序遍历中需要用到 队列 知识

void push_tree(tnode_t *proot)
{queue_t *que = create_queue();push_queue(que,proot);while(!is_empty_queue(que))  //判断队列是否为空，空返回1，非空为0{tnode_t *p;pop_queue(que,&p);printf("%c ",p->data);if(p->pl){push_queue(que,p->pl);} if(p->pr){push_queue(que,p->pr);}}printf("\n");destroy_queue(que);
}

5、获取二叉树的节点个数

int get_tree_node(tnode_t *proot)
{if(!proot)return 0;return get_tree_node(proot->pl) + get_tree_node(proot->pr) + 1;
}

6、获取二叉树的层数 

int get_tree_layer(tnode_t *proot)
{if(!proot)return 0;int cntl = get_tree_layer(proot->pl);int cntr = get_tree_layer(proot->pr);return cntl > cntr ? cntl + 1 : cntr + 1;
} 

 7、销毁二叉树

void destroy_tree(tnode_t *proot)
{if(!proot)return;destroy_tree(proot->pl);destroy_tree(proot->pr);free(proot);
}