力扣3067. 在带权树网络中统计可连接服务器对数目

题目：

给你一棵无根带权树，树中总共有 n 个节点，分别表示 n 个服务器，服务器从 0 到 n - 1 编号。同时给你一个数组 edges ，其中 edges[i] = [ai, bi, weighti] 表示节点 ai 和 bi 之间有一条双向边，边的权值为 weighti 。再给你一个整数 signalSpeed 。

如果两个服务器 a ，b 和 c 满足以下条件，那么我们称服务器 a 和 b 是通过服务器 c 可连接的 ：

• a < b ，a != c 且 b != c 。
• 从 c 到 a 的距离是可以被 signalSpeed 整除的。
• 从 c 到 b 的距离是可以被 signalSpeed 整除的。
• 从 c 到 b 的路径与从 c 到 a 的路径没有任何公共边。

请你返回一个长度为 n 的整数数组 count ，其中 count[i] 表示通过服务器 i 可连接 的服务器对的 数目 。

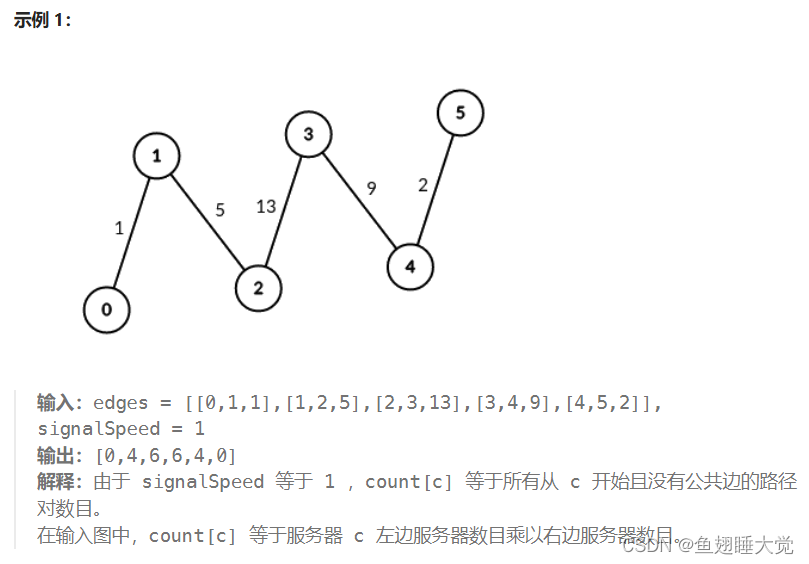
提示：

• 2 <= n <= 1000
• edges.length == n - 1
• edges[i].length == 3
• 0 <= ai, bi < n
• edges[i] = [ai, bi, weighti]
• 1 <= weighti <= 106
• 1 <= signalSpeed <= 106
• 输入保证 edges 构成一棵合法的树。

思路：

1. 首先对图建立邻接表graph。

2. “计算每个节点能连接的节点对的数量ans[i]” ----> 轮流将每个节点i设为根节点，计算出其m个子树中可被连接的节点数，记为cnt[0], cnt[1], ..., cnt[m-1]，那么可推出公式：

即每个括号中的值为：当前子树中可连接的节点数cnt与之前所有子树中可连接的节点数之和s相乘。

代码如下（虽然今天是中等题，但还是想了好久T T）：

class Solution:def countPairsOfConnectableServers(self, edges: List[List[int]], signalSpeed: int) -> List[int]:n = len(edges) + 1   # 节点数ans = [0 for _ in range(n)]# 图的邻接表graph = [[] for _ in range(n)]for edge in edges:graph[edge[0]].append([edge[1], edge[2]])graph[edge[1]].append([edge[0], edge[2]])def dfs(parent, node, weight):   # 返回这一棵子树中可以被整除的节点数if weight % signalSpeed == 0:cnt = 1else:cnt = 0for x, w in graph[node]:if x != parent:cnt += dfs(node, x, weight+w)return cntfor i in range(n):s = 0if len(graph[i]) > 1:    # 如果节点i只与1个节点相连，那它一定没有能连接的节点对for node, weight in graph[i]:cnt = dfs(i, node, weight)# 当前子树中可连接的节点数cnt与之前所有子树中可连接的节点数s相乘，加至ans[i]，并更新s=s+cntans[i] += s * cnts += cntreturn ans

提交通过：