完全背包
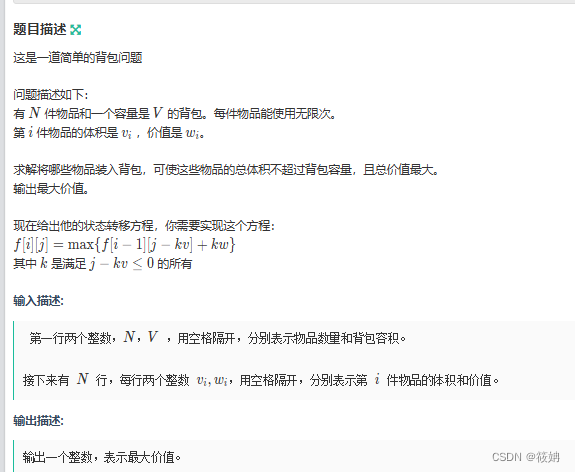
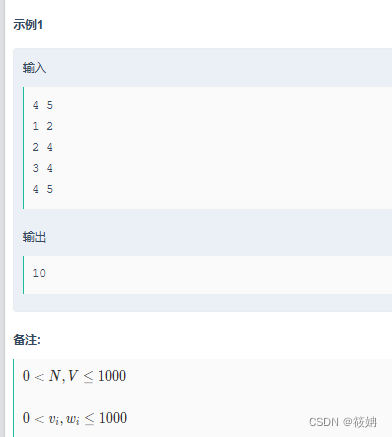
题目描述
运行代码
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int N=1e3+3;
int n,V;
int v[N],w[N],dp[N];
int main(){cin>>n>>V; int t=1;while(t--){for(int i=1;i<=n;++i){cin>>v[i]>>w[i];}memset(dp,-0x3f,sizeof(dp));dp[0]=0;int Max=0;for(int i=1;i<=n;++i){for(int j=v[i];j<=V;++j){dp[j]=max(dp[j],dp[j-v[i]]+w[i]);Max=max(Max,dp[j]);}}cout<<(dp[V]>0?dp[V]:0)<<endl;
}
}
代码思路
-
头文件和命名空间:
- 使用了
#include<bits/stdc++.h>,这是一个常用的头文件,包含了C++标准库中的大部分内容,但这不是一个推荐的做法,因为它会增加编译时间和可能引入不必要的开销。更推荐按需引入所需的头文件,如#include<vector>、#include<algorithm>等。 using namespace std;虽方便,但在大型项目中可能导致命名冲突,建议在具体地方使用std::前缀代替。
- 使用了
-
常量定义:
const int N=1e3+3;定义了数组的最大长度,这是合理的,但如果明确知道背包的最大容量或物品数量,可以进一步精确此常量。 -
主循环意义不明:代码中的
while(t--)循环只执行一次,且t的值没有定义和改变,这个循环是冗余的,可以直接去除。 -
动态规划核心逻辑:
- 动态规划数组
dp[N]初始化为负无穷大,表示未放入任何物品时的价值。 dp[j] = max(dp[j], dp[j-v[i]] + w[i])是动态规划转移方程,表示考虑第i件物品时,容量为j的背包能装入的最大价值。- 优化点在于直接在循环中跟踪最大价值
Max,避免最后再遍历dp[]数组寻找最大值。
- 动态规划数组
-
输出处理:
cout<<(dp[V]>0?dp[V]:0)<<endl;判断如果背包满载时的最大价值大于0,则输出该值,否则输出0,处理了背包容量不足以装入任何物品的情况。
改进思路
- 移除了无用的
while(t--)循环。 - 修改了动态规划数组的遍历顺序,从大到小遍历
j,避免了重复计算,提高了效率。 - 明确了头文件的引入,移除了
#include<bits/stdc++.h>,虽然在这个简短代码中未直接体现,但在实践中是个好习惯。 - 使用了
<climits>头文件中的INT_MIN(或直接写成-0x3f3f3f3f)代替-0x3f来初始化,更符合常规做法,虽然在这个案例中直接初始化为0也足够,因为dp数组的初始状态本应为0。














