中国十大门窗品牌有哪些_能引流的都有什么平台_域名注册需要什么条件_产品软文是什么

目录

669. 修剪二叉搜索树

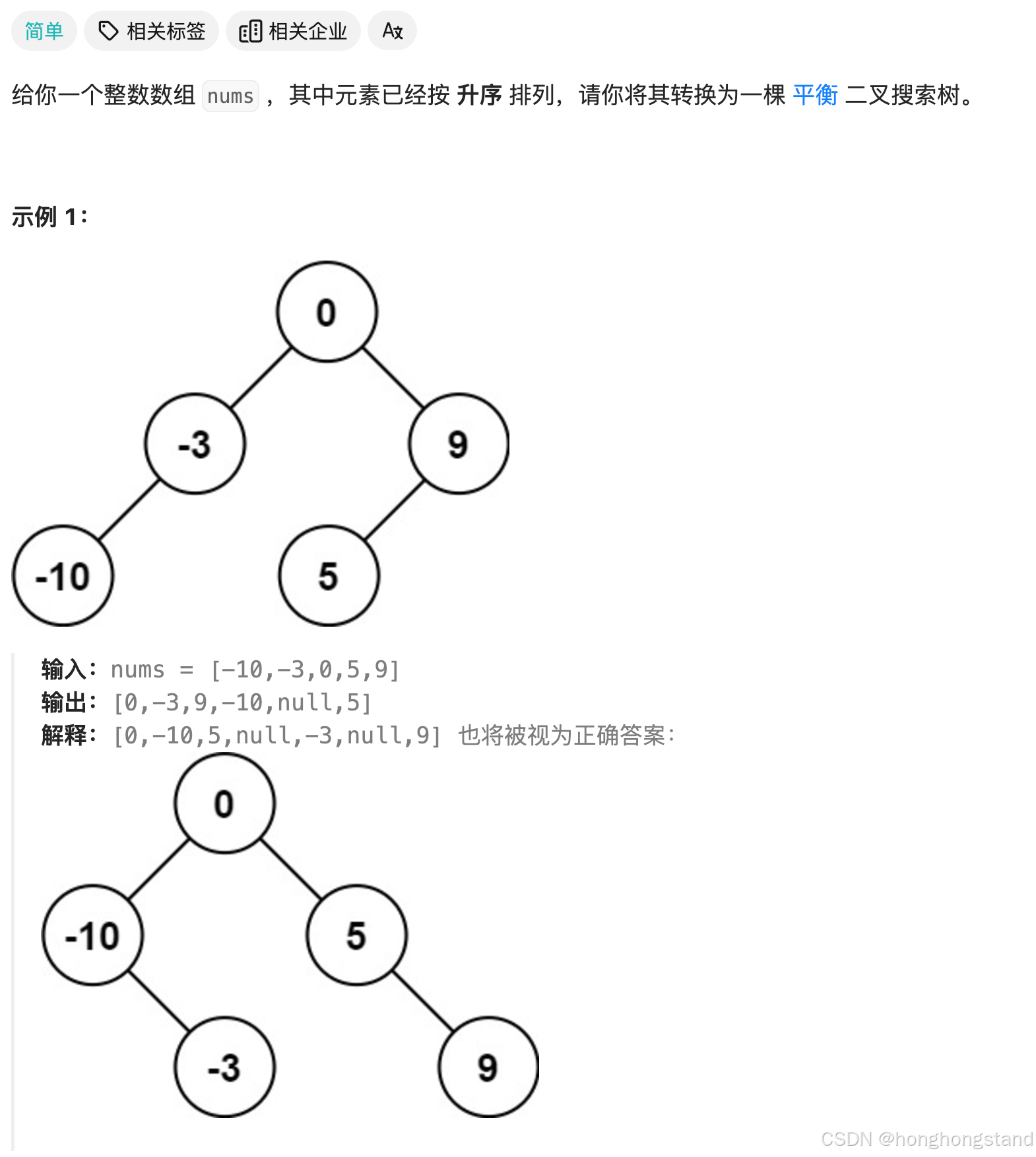
108. 将有序数组转换为二叉搜索树

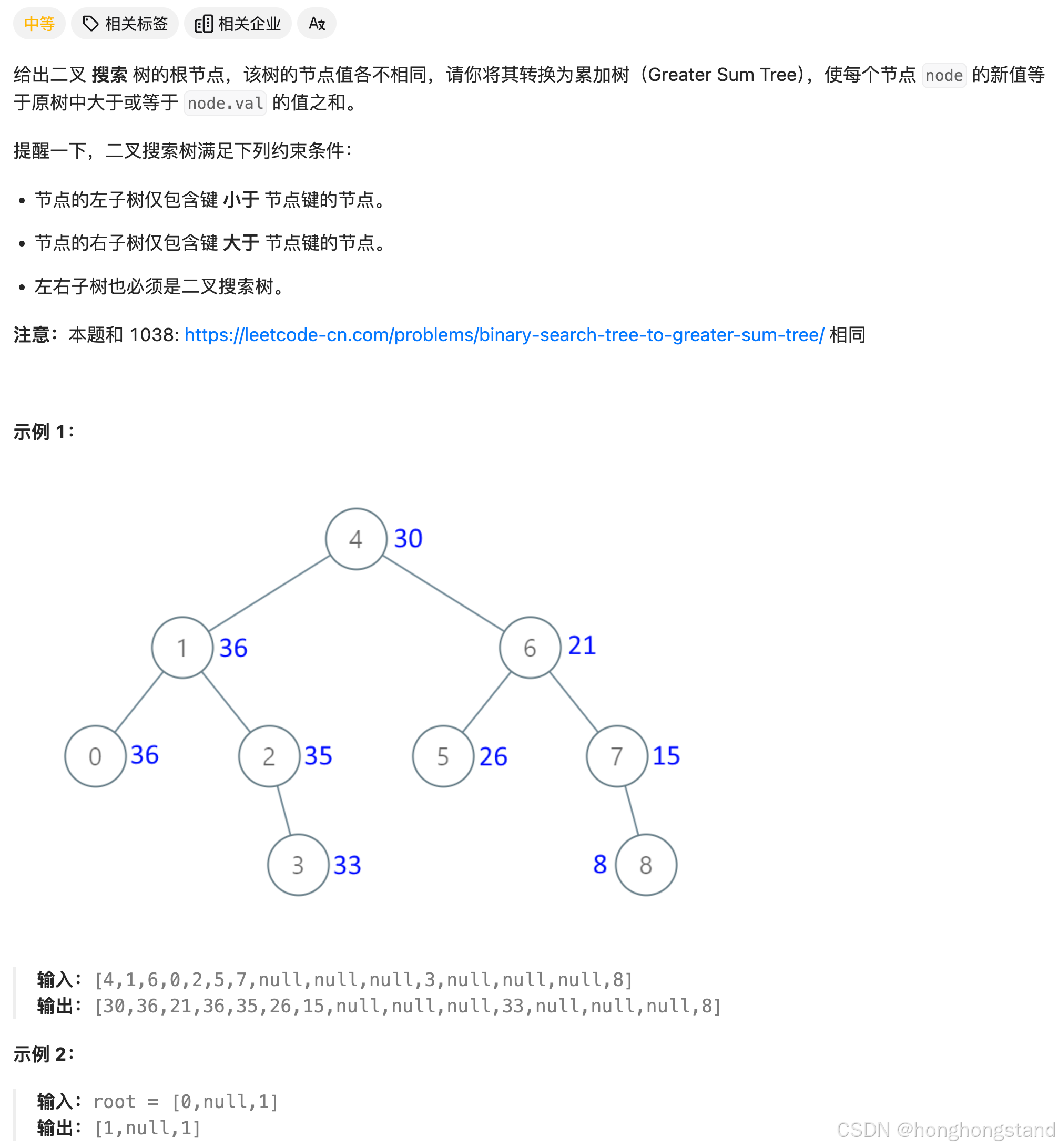
538. 把二叉搜索树转换为累加树

---

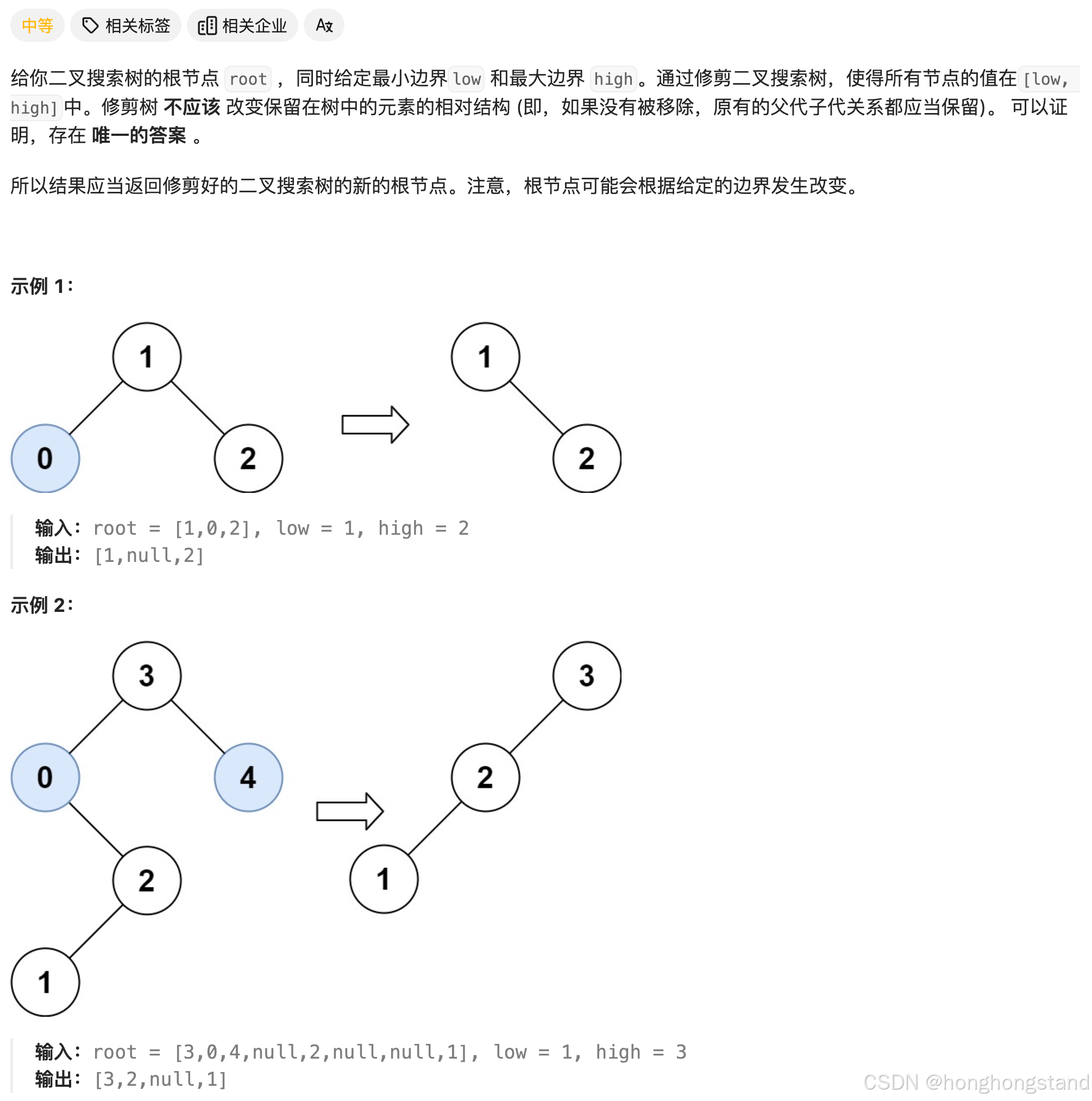
669. 修剪二叉搜索树

要点：

上一篇的最后一题中涉及到了二叉树节点的删除，以本题中第二个例子中的节点0为例，想要删除节点0，需要让3的left指向2，以此完成节点的删除。本题在修剪时的思路是相似的，不在区间内的节点是不能通过直接返回null来删除的，而是需要对节点以及孩子节点进行判断后再重新设置指向。

举例，节点0小于区间下界，那么假设0有左右两个子树，左孩子一定是小于下界的，而右孩子可能位于区间内。因此，此时应该向右遍历，找到符合条件的节点，在这里继续进行递归（因为右子树中可能存在不符合要求的左孩子节点）。

解法：

本质上是删除节点操作新增了更多需要考虑的条件，递归方法中使用前序遍历

1. 输入输出：输入 root，low，high；输出 左右子树进行区间过滤后的root

2. 终止条件：root为none时，代表遍历到了叶子节点，返回空值

3. 单步逻辑：对中节点的左右孩子分别寻找符合区间要求的节点并返回，对中节点的左右孩子套用递归，并赋值为符合要求的节点，最后返回根节点。

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:if root is None:return Noneif root.val < low:# 此处需要套用一次递归，以确保所有子节点符合要求return self.trimBST(root.right, low, high)if root.val > high:return self.trimBST(root.left, low, high)root.left = self.trimBST(root.left, low, high)root.right = self.trimBST(root.right, low, high)return root

108. 将有序数组转换为二叉搜索树

要点：

题目强调平衡二叉搜索树，是防止直接使用链式的方式得到结果。

选取根节点时，选中节点作为根节点可以保持两边的节点数量一致。当数组长度是偶数时，选取偏左或偏右节点都可以，只要在构建时遵循二叉搜索树的规则即可。

解法：

1. 输入输出：输入切分的数组 过程中对root指向进行操作

2. 终止条件：抵达叶子结点终止

3. 单层逻辑：1. 找到中间节点，2. 切分数组，3. 进入下一层递归

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:if len(nums) == 0:return None# 使用整除做切分mid = len(nums) // 2root = TreeNode(nums[mid])# 利用python切片便利的优势，无需指定头尾索引位置root.left = self.sortedArrayToBST(nums[:mid])root.right = self.sortedArrayToBST(nums[mid + 1:])return root

538. 把二叉搜索树转换为累加树

要点：

假设有一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]，问题就变得简单了。可以看到求累加数组的遍历顺序是右中左，那么这个遍历顺序实际是一个反中序遍历。

解法：

由于是倒序的累加，因此在遍历当前节点时，需要在递归中维护上一个节点的值，以此来保证准确。

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:# 右叶子节点的子节点self.pre = 0self.traversal(root)return rootdef traversal(self, cur):if cur is None:return # 先对右子树进行递归self.traversal(cur.right)# 运行累加，直接修改节点值，最后返回rootcur.val += self.preself.pre = cur.val# 对左子树进行递归self.traversal(cur.left)