dp经典问题：LCS问题

dp：LCS问题

最长公共子序列（Longest Common Subsequence, LCS）问题 是寻找两个字符串中最长的子序列，使得这个子序列在两个字符串中出现的相对顺序保持一致，但不要求连续。

力扣原题链接

1.定义

给定两个字符串 S1和S2
$$S1=a_1{a}_2{a}_3...a_n\to 长度为n的字符串$$
$$S2=b_1{b}_2{b}_3...b_m\to 长度为m的字符串$$

子序列(Subsequence)

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在 不改变字符的相对顺序 的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

对于 S1 来说

$$S_{sub}=a_i...a_j\leftarrow i<j,S_{sub}\in S1$$

比如说

$$S_1=abcdfgh$$

$$S_2=abdfhr$$

$$S_1\cap S_2=abdfh$$

2. 动态规划解法

Step1 分析子问题

对于每个子问题都要求出到当前两个子字符串的最长公共子序列。

Step2 状态定义

令 dp[i][j] 表示 text1 的前 i 个字符与 text2 的前 j 个字符的最长公共子序列长度。

Step3 递推求解

1. 初始化状态：

   • 当 i == 0 或 j == 0 时，dp[i][j] = 0，因为任意一个空字符串与另一个字符串的最长公共子序列长度为 0。

2. 状态转移方程：

$$dp[i][j]=\{\begin{array}{ll}dp[i-1][j-1]+1& \text{if }\text{text1[i] = text2[j]}\\ \max (dp[i-1][j],dp[i][j-1])& \text{if }\text{text1[i] = text2[j]}\end{array}$$

示例

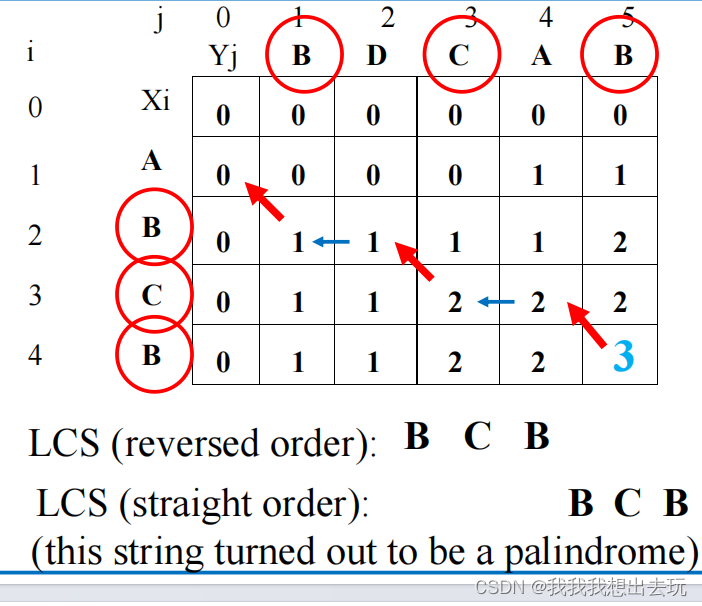
动态规划代码实现

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m = text1.size();int n = text2.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[m][n];}
};

递归代码实现
递归调用的开销会很大，力扣这个题会超时

class Solution{int longestCommonSubsequence(string text1, string text2) {return rec(text1,text2,text1.size()-1,text2.size()-1);}int rec(const&string str1,const&string str2,int m,int n){if(m==0||n==0)return 0;if(str1[m]==str[n]){return 1+rec(str1,str2,m-1,n-1);}else{return max(rec(str1,str2,m-1,n),rec(str1,str2,m,n-1));}}
}