给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格(不必相邻)。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。
你可以从 任一 单元格开始,并且必须至少移动一次。
返回你能得到的 最大 总得分。
示例 1:

输入:grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]
输出:9
解释:从单元格 (0, 1) 开始,并执行以下移动:
- 从单元格 (0, 1) 移动到 (2, 1),得分为 7 - 5 = 2 。
- 从单元格 (2, 1) 移动到 (2, 2),得分为 14 - 7 = 7 。
总得分为 2 + 7 = 9 。
示例 2:
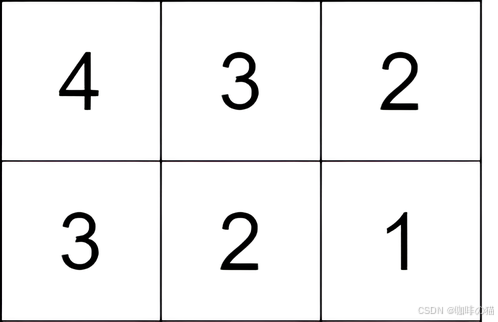
输入:grid = [[4,3,2],[3,2,1]]
输出:-1
解释:从单元格 (0, 0) 开始,执行一次移动:从 (0, 0) 到 (0, 1) 。得分为 3 - 4 = -1 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 1051 <= grid[i][j] <= 105
问题简要描述:返回最大总得分
细节阐述:
- f[i][j] 表示以 (i,j) 为终点的路径的最小值
Java
class Solution {public int maxScore(List<List<Integer>> grid) {int m = grid.size(), n = grid.get(0).size();int[][] f = new int[m + 1][n + 1];int inf = 1 << 30, ans = -inf;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {int min = inf;if (i > 0) {min = Math.min(min, f[i - 1][j]);}if (j > 0) {min = Math.min(min, f[i][j - 1]);}ans = Math.max(ans, grid.get(i).get(j) - min);f[i][j] = Math.min(grid.get(i).get(j), min);}}return ans;}
}Python3
class Solution:def maxScore(self, grid: List[List[int]]) -> int:f = [[0] * len(grid[0]) for _ in range(len(grid))]ans = -inffor i, row in enumerate(grid):for j, x in enumerate(row):mi = infif i:mi = min(mi, f[i - 1][j])if j:mi = min(mi, f[i][j - 1])ans = max(ans, grid[i][j] - mi)f[i][j] = min(grid[i][j], mi)return ansTypeScript
function maxScore(grid: number[][]): number {const [m, n] = [grid.length, grid[0].length];const f = Array.from({length: m}, () => Array.from({length: n}, () => 0));let ans = -Infinity;for (let i = 0; i < m; i++) {for (let j = 0; j < n; j++) {let min = Infinity;if (i > 0) {min = Math.min(min, f[i - 1][j]);}if (j > 0) {min = Math.min(min, f[i][j - 1]);}ans = Math.max(ans, grid[i][j] - min);f[i][j] = Math.min(grid[i][j], min);}}return ans;
};C++
class Solution {
public:int maxScore(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();int f[m][n];int inf = 1 << 30, ans = -inf;for (int i = 0;i < m;i++) {for (int j = 0;j < n;j++) {int mi = inf;if (i > 0) {mi = min(mi, f[i - 1][j]);}if (j > 0) {mi = min(mi, f[i][j - 1]);}ans = max(ans, grid[i][j] - mi);f[i][j] = min(grid[i][j], mi);}}return ans; }
};Go
func maxScore(grid [][]int) int {m, n := len(grid), len(grid[0])f := make([][]int, m)for i := range f {f[i] = make([]int, n)}const inf int = 1 << 30ans := -inffor i, row := range grid {for j, x := range row {mi := infif i > 0 {mi = min(mi, f[i-1][j])}if j > 0 {mi = min(mi, f[i][j-1])}ans = max(ans, x-mi)f[i][j] = min(x, mi)}}return ans
}










——动态规划)


