汶上网站开发_品牌视觉形象设计案例_广州网络营销选择_凡科网建站系统源码

参考：

《A Tour of Survival Analysis from Classical to Modern》

https://onlinelibrary.wiley.com/doi/abs/10.1002/sim.2427

[George H. Chen ,Carnegie Mellon University][ Assistant Professor of Information Systems]

生存分析是统计学的一个分支，用于分析一个或多个事件发生前的预期持续时间。在工程学中，该主题称为可靠性分析；在经济学中，该主题称为持续时间分析或持续时间建模或事件发生时间分析；在社会学中，该主题称为事件历史分析。生存分析试图回答以下问题：

在给定时间内存活的人口比例
死亡率
预测因子如何解释事件发生时间分析
常用生存分析模型

Kaplan-Meier Analysis

Cox Proportional Hazards Model

Log-Logistic Parametric Model

Weibull Model

Survival Tree Analysis

Survival Random Forest

常用的生存分析的模型

目录：

典型的理论设定
Censoring
Lift Tabel
Example of a Survival Estimator
Kaplan-Meier Estimator (1958)
Kaplan-Meier Estimator Python 例子

一典型的理论设定

假设数据点 (x1, y1, 𝛿1), (x2, y2, 𝛿2), …, (xn, yn, 𝛿n) 是独立同分布（iid）生成的：

特征向量 $x_i$ 是从特征分布中采样得到的
真实生存时间 $z_i$ 和真实删失时间 $c_i$ 是在给定 $x_i$ 的条件下进行采样的，且在给定 $x_i$ 的条件下， $z_i$ 和 $c_i$ 是条件独立的。
如果 $z_i$ ≤ $c_i$ （event occur）：
$y_i=z_i$ ，事件指示符 𝛿i = 1。
否则(event did not occur）：
$y_i=c_i$ ，事件指示符 𝛿i = 0。

二 Censoring

参考： youtube 搬运| Survival Analysis_哔哩哔哩_bilibili

删失（Censoring）是一个关键概念，用于处理未观察到事件确切时间的数据。

以员工离职与在职（员工留存）为例：

完全观测数据 event_observed

定义：事件（如员工离职）在研究期间内明确发生，且时间点被准确记录。

示例：某员工在入职后 3 年辞职，研究记录了他的离职时间。

Censoring 主要分为下面三种情况：

1 Right-censoring （Right-Censoring，最常见）

定义：在研究结束时，某些个体尚未发生目标事件（如员工仍在职），因此其真实“生存时间”未知。

可能原因：

员工 仍在职（研究结束时未离职）；

员工 中途退出研究（如提前离职但原因与研究无关）；

数据 跟踪丢失（如员工失联）

示例：某员工入职 5 年后研究结束，他仍在职，其离职时间未被观测到

2 Left-Censoring 左删失（Left-Censoring，较少见）

定义：事件发生在研究开始之前，但确切时间未知。

示例：研究员工“离职”，但部分员工在研究开始时 已经离职，具体离职时间不明。

3 Interval-Censored cases 区间删失

定义：仅知道事件发生在某个时间区间内，而非精确时间点。

示例：员工在 第2年和第3年之间离职，但具体日期未记录。

4 为什么需要处理删失数据

避免偏差：若忽略仍在职的员工（右删失），仅分析已离职者，会低估平均留存时间。

以机器学习 Liner regression 为例，训练出来的即使拟合度非常好，但是也是有问题的

统计方法支持：生存分析工具（如 Kaplan-Meier 曲线、Cox 比例风险模型）可有效利用删失数据，提供更准确的估计。

三 Life Tabel（Survival Table Components）

生存表展示了在特定时间点结束时“幸存者”的比例.

在生存表中，时间间隔的宽度会影响生存率/生存概率，因此明智且审慎地选择间隔大小很重要。youtube 搬运| Survival Analysis_哔哩哔哩_bilibili

3.1 Interval【or durations】 : 感兴趣的时间间隔

Interval[i=1]= 0-29 days

Interval[i=2]= 30-59 days

Interval[i=3]= 60-89 days

当i=1,对应 0-29天的event

3.2 $n_i$ 参与研究的人数

$n_0=120$ 该时间间隔内, 120人开始这项的研究
$n_1=103$ 该时间间隔内, 103人开始这项的研究
$n_1=100$ 该时间间隔内, 100人开始这项的研究

3.3 ： censor number: 在interval[i] 区间内被截尾（右截尾）的案例数量

3.4 . 校正风险人数(Adjusted Number at Risk 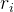$r_i$ )

定义：在给定时间区间内，经过删失调整后实际面临事件（如离职、死亡）风险的案例数。

计算公式：

其中：

$n_i$ = 时间区间起始时的总案例数

$c_i$ = 该区间内删失的案例数（如失访、研究终止时仍存活）

Example:

3.5 . 事件发生数（Number of Events $d_i)$

定义：在该时间区间内，实际发生目标事件（如员工离职、设备故障）的案例数量。

示例：
$d_0=15$ （观察到15例事件）

3.6 事件发生概率（Event Probability 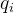$q_i$ )

定义：在风险人群中，该区间内发生事件的比例。

计算公式：

后面代码里面都是直接用 $q_i =\frac{d_i}{n_i}$

示例：

3.7 . 生存概率（Survival Probability $p_i$ )

定义：在风险人群中，该区间内未发生事件的比例。

计算公式：

示例：

5. 累积生存率（ Cumulative Survival 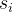$s_i$ )

定义：截至当前时间区间结束时，案例仍未发生事件的总体概率（即"存活"至今的累积概率）。

计算公式：

其中 Si−1Si−1 表示前一区间的累积生存率。

注：初始时 $S_0=1$ (基线存活率100%）

# -*- coding: utf-8 -*-
"""
Created on Wed Apr  9 17:45:00 2025@author: chengxf2
"""import pandas as pd
liftTabel = {'Interval':['0-29 days', '30-59 days', '60-89 days'], 'n':[120, 103, 100],'c:Censoring':[2,1,10],'r:Adjusted Number at Risk':[0,0, 0],'d:Number of Events':[15,2,15],'q:Event Probability':[0,0,0],'p:Survival Probability':[0,0,0],'s:Cumulative Survival':[-1,12,33]}df = pd.DataFrame(liftTabel)#for index , row in df.iterrows():#print(f"i: {index},  n: {row['n']}")
df['r:Adjusted Number at Risk']=df['n']-df['c:Censoring']/2.0
print("\n 校正风险人数 \n ", df['r:Adjusted Number at Risk'])df['q:Event Probability']=df['d:Number of Events']/df['r:Adjusted Number at Risk']
print("\n 事件发生的概率 \n", df['q:Event Probability'])df['p:Survival Probability']= 1.0 - df['q:Event Probability']
print("\n 生存的概率 \n", df['p:Survival Probability'])for index , row in df.iterrows():if index == 0:s_pre = 1.0else:s_pre =  df.iloc[index-1, 7]#df['p:Survival Probability']p = df.iloc[index,6] s = p*s_predf.iloc[index, 7] = s
pd.options.display.float_format = '{:.2f}'.formatprint(df['s:Cumulative Survival'])

四经典估计量及预测误差评估

跟临床医生沟通过，他们论文常用的就一种方案。

step1 : 找出所有出现死亡事件的独特时间点

按照死亡时间点排序L = # unique times of death

step2: 建立表

step3: 我们可以得到下图，横坐标表示时间，纵坐标表示生存时间超过时间t的概率

比较经典的就是Kaplan-Meier

五 Kaplan-Meier估计量（Kaplan-Meier Estimator, 1958）

使用lifelines库（需安装：pip install lifelines）分析员工离职数据。

1. 基本概念

Kaplan-Meier估计量（又称乘积限估计量）是一种非参数统计方法，用于估计生存函数（Survival Function），即在给定时间点个体仍未发生目标事件（如死亡、故障、离职等）的概率。其核心特点是能够处理右删失数据（Right-Censored Data）。

2. 核心公式

生存函数的Kaplan-Meier估计公式为

$t_i$ ： duration time (持续时间)
$d_i$ ：number of events happend at time $t_i$ ( 在时间点 $t_i$ 发生的事件数量)
$n_i$ ：number of individuals known to have survied up to time $t_i$
已知存活至时间点 $t_i$ 的个体数量

Kaplan-Meier估计量具有诸多优势，包括直观易懂、操作简单，且能灵活适用于任何时间-事件数据。这些优点使其成为处理新数据时首选的初始模型。然而，其生存曲线通常不平滑，且当超过50%的数据被截尾时，无法计算中位生存时间。最后，若需分析协变量如何影响生存函数，则需要借助其他模型。

六 Kaplan-Meier Estimator Python 例子

假设5个病人的生存时间（月）和事件状态如下，按时间升序排列：

病人	时间 duration	event_observed（1=发生，0=截尾）
1	2	1
2	3	0
3	5	1
4	8	1
5	10	0

# -*- coding: utf-8 -*-
"""
Created on Thu Apr 10 13:47:58 2025@author: chengxf2
"""# -*- coding: utf-8 -*-
"""
Created on Wed Apr  9 17:45:00 2025@author: chengxf2
"""
import pandas as pd
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt#假设有一组员工的在职时间time（月）
#eent: 是否离职（1=离职，0=删失）：# 0表示删失（如研究结束时仍在职）
data = pd.DataFrame({"durations": [ 3, 5, 10, 10, 12],  # t=10 时有 2 个事件"event_observed": [1, 1, 1,  0,  0]      # 1=事件，0=删失
})
# 初始化模型
kmf = KaplanMeierFitter()# 拟合数据（时间列和事件列）
kmf.fit(durations=data["durations"], event_observed=data["event_observed"])# 查看每个时间点的风险人数
print("\n 查看每个时间点的风险人数 : ",kmf.event_table.at_risk)
# 输出生存概率表
print("\n 输出生存概率表: ",kmf.survival_function_)# 绘制生存曲线
kmf.plot_survival_function()
plt.title("Kaplan-Meier Survival Curve (Employee Retention)")
plt.ylabel("Survival Probability")
plt.xlabel("Time (Months)")
plt.grid()
plt.show()

Example of a Survival Estimator

Fitting a Kaplan-Meier estimator | Python

https://www.youtube.com/watch?v=t6vdjwhauF8

youtube 搬运| Survival Analysis_哔哩哔哩_bilibili

R语言生存分析Survival analysis原理与晚期肺癌患者分析案例_哔哩哔哩_bilibili

https://www.youtube.com/watch?v=gvgzPEcKSL8

https://www.youtube.com/watch?v=fHctWWjc8os

https://www.youtube.com/watch?v=q-CGbakKD-Y

https://www.youtube.com/watch?v=PH2o_KVF7Jw

https://www.youtube.com/watch?v=Os1jikCZTvg

https://zhuanlan.zhihu.com/p/661488887

When Should You Use Non-Parametric, Parametric, and Semi-Parametric Survival Analysis – Boostedml