💛前情提要💛
本文是传知代码平台中的相关前沿知识与技术的分享~
接下来我们即将进入一个全新的空间,对技术有一个全新的视角~
本文所涉及所有资源均在传知代码平台可获取
以下的内容一定会让你对AI 赋能时代有一个颠覆性的认识哦!!!
以下内容干货满满,跟上步伐吧~
📌导航小助手📌
- 💡本章重点
- 🍞一. 概述
- 🍞二. 核心算法
- 🍞三. 关键代码
- 🍞四. 运行方法
- 🍞五.运行结果
- 🫓总结
💡本章重点
- 基于曲率的图重新布线
🍞一. 概述
论文链接
Topping, Jake, et al. “Understanding over-squashing and bottlenecks on graphs via curvature.” arXiv preprint arXiv:2111.14522 (2021).
大多数图神经网络(Graph Neural Networks, GNN)使用消息传递范式,其中节点特征在输入图上传播。最近的研究表明,来自远距离结点的信息流失真,是限制依赖远程交互的任务的消息传递效率的重要因素。
该限制被称为“过度挤压”(Over-squashing)。过度挤压的原因在于,图中每个结点的k跳邻居的数量随着k的增长而指数级增长,远距离结点的信息难以压缩到固定大小的结点特征中,从而导致信息丢失。本文提供了对GNN中过度挤压现象的精确描述,并分析了它是如何从图中的瓶颈产生的。
为此,本文引入了一种新的基于边的组合曲率,并证明了负曲率边是导致过度挤压问题的原因。本文还提出了一种基于曲率的图重现布线方法,以缓解过度挤压问题。
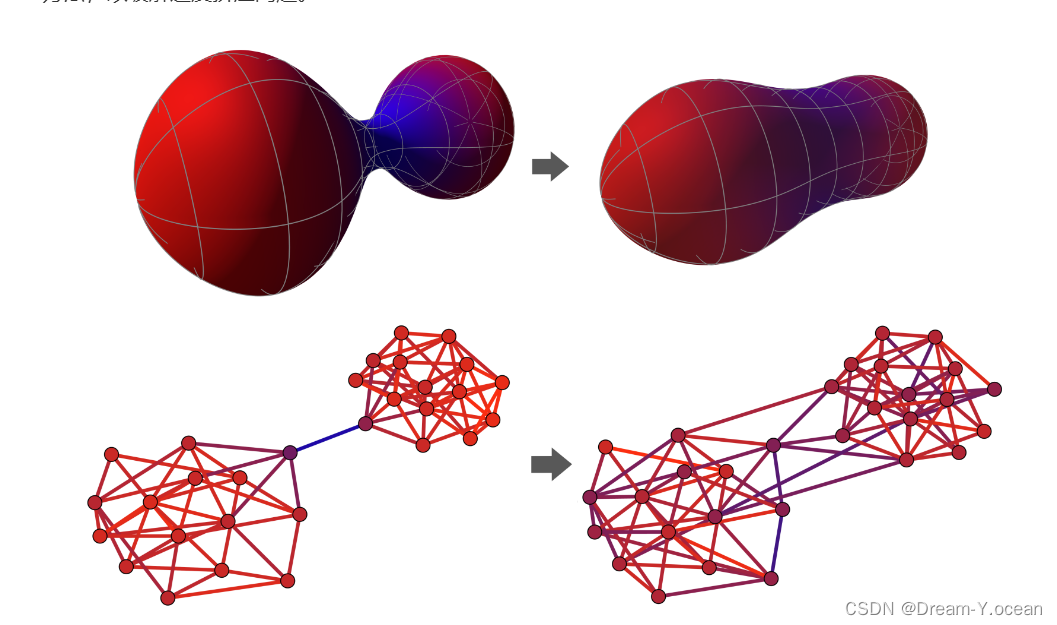
上图:曲面上曲率的演变可能会减少瓶颈。
下图:本文展示了如何在图上做同样的事情来提高GNN的性能。蓝色代表负曲率;红色代表正曲率。
🍞二. 核心算法
算法说明

- 黎曼几何中的一个自然对象是里奇曲率(Ricci curvature),这是一种决定测地线色散的双线性形式,即从“相同”速度的附近点开始的测地线是否保持平行(欧几里得空间)、收敛(球面空间)或发散(双曲空间)。
- 算法在每次迭代中都会添加一条边来支持图中最负曲率的边,然后移除最正曲率的边。
- 原始输入图和重新布线图之间的图编辑距离以
max number of iterations的 2 倍为界。 - 移除曲率最大的边是为了平衡曲率和结点的度的分布。
🍞三. 关键代码
def sdrf(data, max_iterations=10, remove_edges=True, remove_bound=0.5, tau=1.0, undirected=True):# 1. 将torch_geometric.data.Data实例转化为networkx.DiGraph实例,方便后续加边、减边操作G = to_networkx(data)if undirected:G = G.to_undirected()# 2. 获取图信息(邻接矩阵,边的个数)edge_index = data.edge_indexif undirected:edge_index = to_undirected(edge_index)A = to_dense_adj(remove_self_loops(edge_index)[0])[0] # 邻接矩阵A = A.cuda()N = A.shape[0] # 边的个数C = torch.zeros(N, N).cuda() # 初始化Ricci曲率矩阵,即Ric(i, j)# 3. 进入图的加边、减边循环过程,其中max_iterations为最大迭代次数for x in range(max_iterations):can_add = True# 3.1 根据BFC算法更新Ricci曲率矩阵balanced_forman_curvature(A, C=C)ix_min = C.argmin().item()x = ix_min // Ny = ix_min % N# 3.2 计算可加边的候选集candidatesif undirected:x_neighbors = list(G.neighbors(x)) + [x]y_neighbors = list(G.neighbors(y)) + [y]else:x_neighbors = list(G.successors(x)) + [x]y_neighbors = list(G.predecessors(y)) + [y]candidates = []for i in x_neighbors:for j in y_neighbors:if (i != j) and (not G.has_edge(i, j)):candidates.append((i, j))# 3.3 根据边添加之后对Ricci曲率的提升程度,从候选集中选择边k~l进行添加if len(candidates):D = balanced_forman_post_delta(A, x, y, x_neighbors, y_neighbors)improvements = []for i, j in candidates:improvements.append((D - C[x, y])[x_neighbors.index(i), y_neighbors.index(j)].item())k, l = candidates[np.random.choice(range(len(candidates)), p=softmax(np.array(improvements), tau=tau))]G.add_edge(k, l) # 添加边if undirected:A[k, l] = A[l, k] = 1else:A[k, l] = 1else:can_add = Falseif not remove_edges:break# 3.4 移除具有最大Ricci曲率的边,其中remove_bound为曲率最大上界if remove_edges:ix_max = C.argmax().item()x = ix_max // Ny = ix_max % Nif C[x, y] > remove_bound:G.remove_edge(x, y) # 移除边if undirected:A[x, y] = A[y, x] = 0else:A[x, y] = 0else:if can_add is False:break# 4. 将networkx.DiGraph实例转化为torch_geometric.data.Data实例,返回return from_networkx(G)
🍞四. 运行方法
数据集
支持 Cora, Citeseer, Pubmed, Cornell, Texas, Wisconsin
脚本自动下载。如不能请参考 geom-gcn
配置文件
不同数据集的配置文件位于./configs/。运行之前需要修改数据集根目录和输出目录:
output_dir: $OUTPUT_DIR$
data:root: $DATA_ROOT$
训练和测试
# train on train data splits
python train.py --config-file configs/*.yaml
# test on val and test data splits
python eval.py --config-file configs/*.yaml
search_dir=configs
for file in "$search_dir"/*
dopython train.py --config-file $filepython eval.py --config-file $file
done
🍞五.运行结果
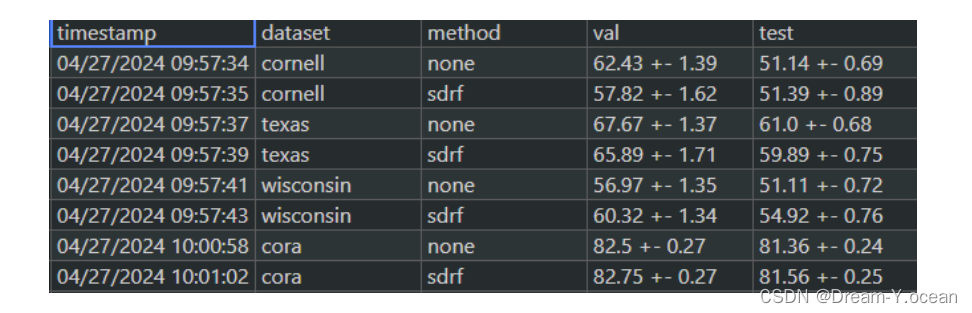
运行日志、模型权重、重新布线结果保存在 $OUTPUT_DIR/$DATASET_NAME/
测试结果(accuracy)保存在 ./result.csv
🫓总结
综上,我们基本了解了“一项全新的技术啦” 🍭 ~~
恭喜你的内功又双叒叕得到了提高!!!
感谢你们的阅读😆
后续还会继续更新💓,欢迎持续关注📌哟~
💫如果有错误❌,欢迎指正呀💫
✨如果觉得收获满满,可以点点赞👍支持一下哟~✨
【传知科技 – 了解更多新知识】














