目录
一、集合框架
1.1 集合框架的重要性
1.3 容器背后对应的数据结构
1.4 相关 Java 知识
二、算法
2.1 如何衡量一个算法的好坏
2.2 时间复杂度
2.2.1 时间复杂度的概念
2.2.2 大O的渐进表示法
2.2.3 推导大O阶方法
2.2.4 常见时间复杂度举例
2.3 空间复杂度
三、泛型初步
3.1 包装类
3.1.1 基本数据类型和对应的包装类
3.1.2 装箱与拆箱
编辑
编辑
3.1.3 自动装箱与自动拆箱
3.2 什么是泛型
3.2.1 实际应用
3.2.1.1 语法
四、 泛型类
4.1 语法
编辑
4.2 泛型类的类型推导
五、泛型是如何编译的
5.1 擦除机制
六、泛型的上界
6.1 语法
6.2 示例
6.3 复杂示例
6.4 泛型方法
一、集合框架
Java 会把一些数据结构封装起来

这张图描述了 Java 中类与类 类与接口之间的关系
注: 仅描述部分重要的常见类
1.1 集合框架的重要性
1.3 容器背后对应的数据结构
1.4 相关 Java 知识
1. 泛型 Generic
二、算法
2.1 如何衡量一个算法的好坏
2.2 时间复杂度
2.2.1 时间复杂度的概念
2.2.2 大O的渐进表示法
void func1(int N){int count = 0;for (int i = 0; i < N ; i++) {for (int j = 0; j < N ; j++) {count++;}}for (int k = 0; k < 2 * N ; k++) {count++;}int M = 10;while ((M--) > 0) {count++;}System.out.println(count);}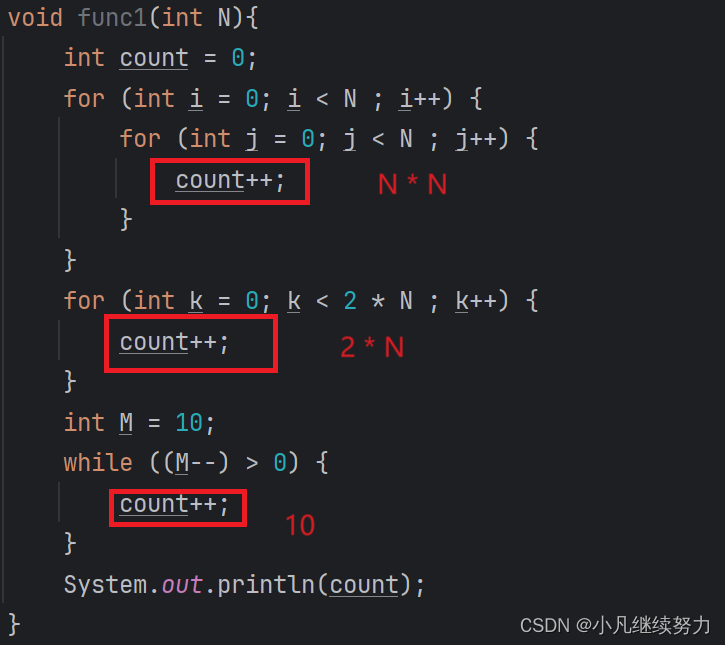
用函数来表示就是
F(N) = N^2 + 2 * N + 10
当N越来越大时,有些项是可以删掉的
2.2.3 推导大O阶方法
使用大O的渐进表示法以后,Func1的时间复杂度为:
O(N^2)
2.2.4 常见时间复杂度举例
void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}
O(N)
void func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; k++) {
count++;
}
for (int k = 0; k < N ; k++) {
count++;
}
System.out.println(count);
} 
O(M+N)
void func4(int N) {
int count = 0;
for (int k = 0; k < 100; k++) {
count++;
}
System.out.println(count);
} 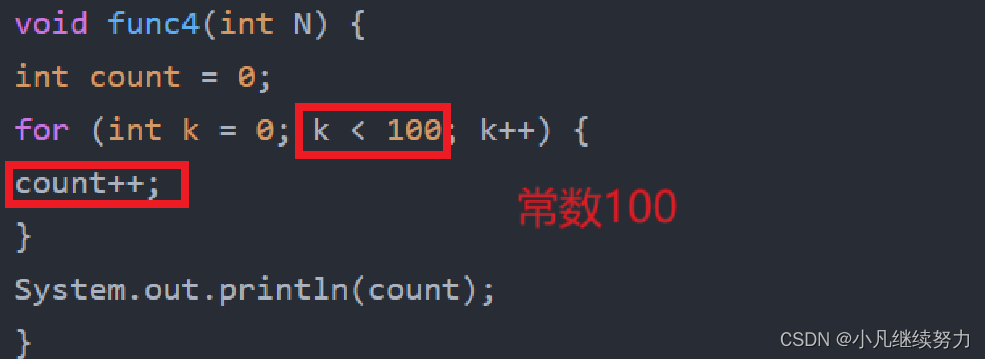
O(1)
void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}}需要注意的是
在计算代码的时间复杂度的时候,不只是看代码
还要结合代码的思想
在冒泡排序中

这里是基本操作
冒泡排序的思想是每一趟会少比较一次
那这个基本操作执行的次数就是
(n - 1) + (n - 2) + ……+ 1
倒着写就是
1 + 2 +…… +(n - 1)
那么这其实就是一个等差数列
和就是
(n^2 - n) / 2
大O阶
O(N^2)
int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1;while (begin <= end) {int mid = begin + ((end-begin) / 2);if (array[mid] < value)begin = mid + 1;else if (array[mid] > value)end = mid - 1;elsereturn mid;}return -1;}对于二分查找来说
每进行一次比较就排除了一半的数据
最坏的情况就是最后一个才被找到

即 n = 1 时是最坏的情况
n / x = 1
那么执行的次数就等于
大O阶
O()
long factorial(int N) {return N < 2 ? N : factorial(N-1) * N;}一般情况下:
递归的时间复杂度 = 递归的次数 * 每次递归后的执行次数
对于这个递归函数,只需要知道他的递归次数就行了
这里递归的条件是 N < 2
那么易得出
递归次数为
N - 1
大O阶
O(N)
int fibonacci(int N) {return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);}对于这个递归函数来说
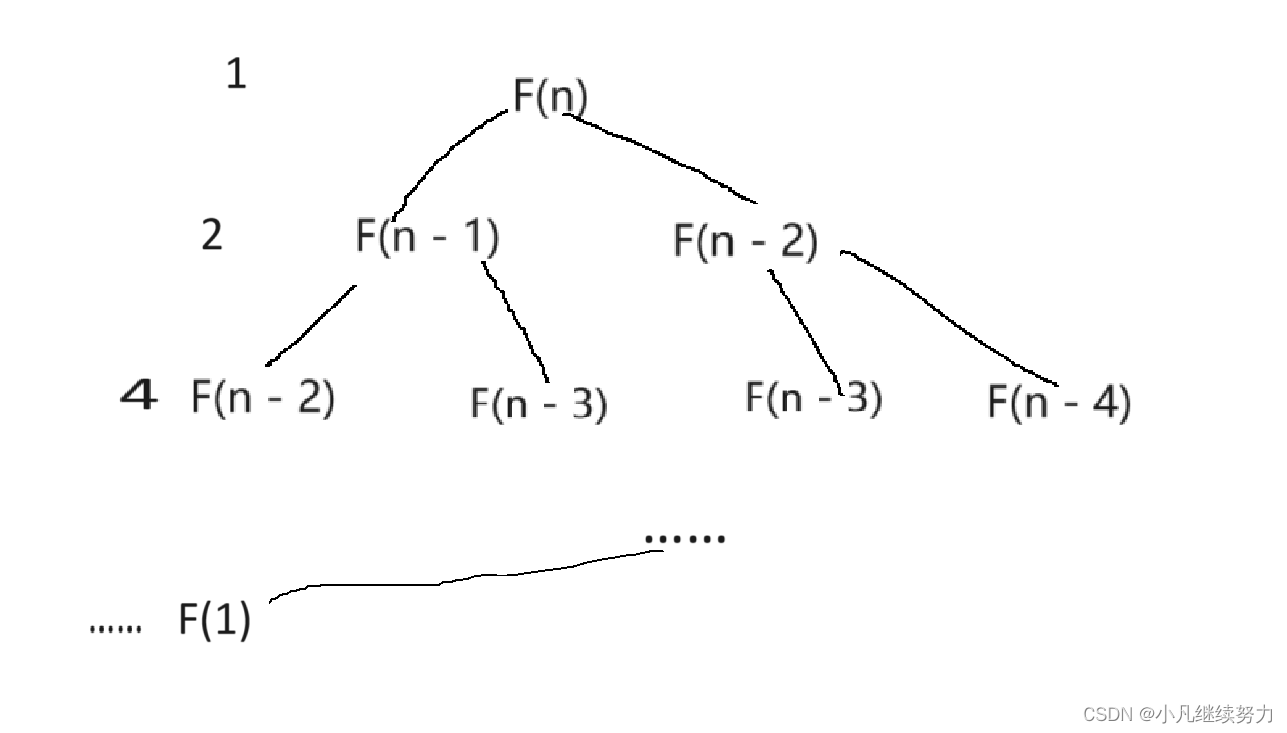
执行次数是1 + 2 + 4 +…… +
即等比数列求和
- 1
大O阶
O()
2.3 空间复杂度
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}
使用了常数个额外空间,所以空间复杂度为 O(1)
int[] fibonacci(int n) {int[] fibArray = new int[n + 1];fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; i++) {fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;}开辟了N个空间
空间复杂度为
O(N)
long factorial(int N) {return N < 2 ? N : factorial(N-1)*N;
}每一次递归都会在栈上开辟一块儿空间
那么空间复杂度为
O(N)
三、泛型初步
3.1 包装类
3.1.1 基本数据类型和对应的包装类
| 基本数据类型 | 包装类 |
| byte | Byte |
| short | Short |
| int | Integer |
| long | Long |
| float | Float |
| double | Double |
| char | Character |
| boolean | Boolean |
3.1.2 装箱与拆箱
将基本类型数据转变为包装类型叫做装箱
public static void main(String[] args) {int i = 1;Integer a = i;Integer b = 2;}
可以看到汇编中调用了方法 Integer.valueOf
将包装类型转变为基本类型叫拆箱
public static void main(String[] args) {Integer a = 1;int i = a;}3.1.3 自动装箱与自动拆箱
上述两代码被称为自动装箱与自动拆箱
有自动就会有手动
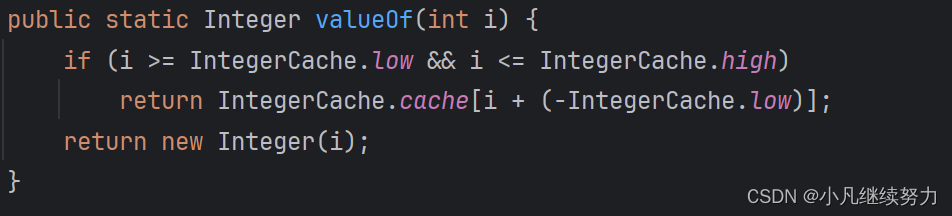
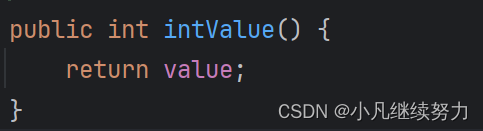
public static void main(String[] args) {int i = 1;Integer a = Integer.valueOf(i);System.out.println(a);Integer b = 2;int j = b.intValue();System.out.println(j);}
这里有一串代码
public static void main(String[] args) {Integer a = 100;Integer b = 100;System.out.println(a == b);Integer c = 200;Integer d = 200;System.out.println(c == d);}

问题是出在这里
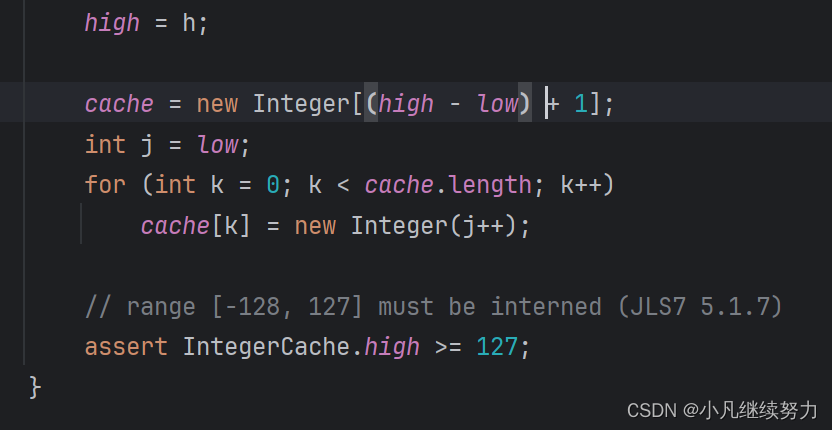
也就是说
小于等于127
大于等于-128的值会被放在 cache 这个数组中

而超出这个范围

将会重新创建一个对象
这说明
包装类对象在进行 == 判断时是比较的地址
创建出来的两个新的对象地址肯定不同
3.2 什么是泛型
3.2.1 实际应用
class MyArray{Object[] array = new Object[10];public void setArray(int pos,Object val){this.array[pos] = val;}public Object getVal(int pos){return this.array[pos];}
}乍一看这么写好像没问题
public class Test3 {public static void main(String[] args) {MyArray myArray = new MyArray();myArray.setArray(0,1);myArray.setArray(1,"hello");String str = myArray.getVal(1);}
}
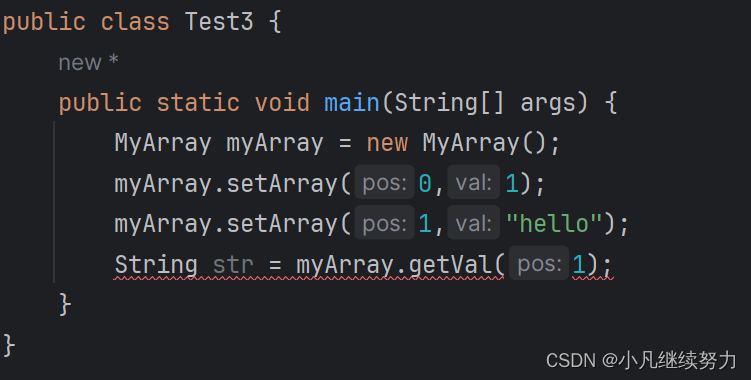
这里还需要强转
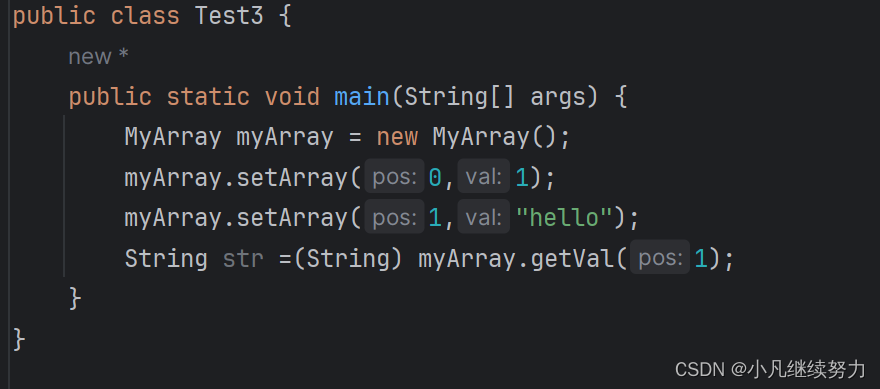
这样虽然说实现了需要的功能
但是很乱,而且在取数据的时候还得观察对应的数据是啥进行强转
那是否可以在实例化对象就指定数组中放什么类型的数据
这样在取的时候就不用判断了
Java 中引入了泛型
3.2.1.1 语法
class 泛型类名称<类型形参列表> {
// 这里可以使用类型参数
}
class 泛型类名称<类型形参列表> extends 继承类/* 这里可以使用类型参数 */ {
// 这里可以使用类型参数
}
class ClassName<T1, T2, ..., Tn> extends ParentClass<T1> {
// 可以只使用部分类型参数
}上述代码可以这样改
class MyArray<T>{Object[] array = new Object[10];public void setArray(int pos,T val){this.array[pos] = val;}public T getVal(int pos){return (T)this.array[pos];//把返回的类强转为指定的类}
}public static void main(String[] args) {MyArray<Integer> myArray = new MyArray<>();myArray.setArray(0,1);myArray.setArray(1,2);int num1 = myArray.getVal(0);int num2 = myArray.getVal(1);System.out.println(num1);System.out.println(num2);MyArray<String> myArray1 = new MyArray<>();myArray1.setArray(0,"hello");myArray1.setArray(1,"world");String str1 = myArray1.getVal(0);String str2 = myArray1.getVal(1);System.out.println(str1);System.out.println(str2);}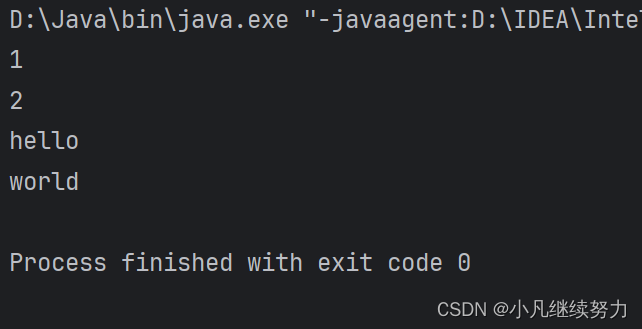
四、 泛型类
4.1 语法
泛型类<类型实参> 变量名; // 定义一个泛型类引用
new 泛型类<类型实参>(构造方法实参); // 实例化一个泛型类对象注意:泛型只能接受类,所有的基本数据类型必须使用包装类!

不能直接 new 一个泛型的数组

如果非要 new 一个泛型数组
可以这样写
public T[] arr =(T[]) new Object[10];但这样写其实只是骗过编译器
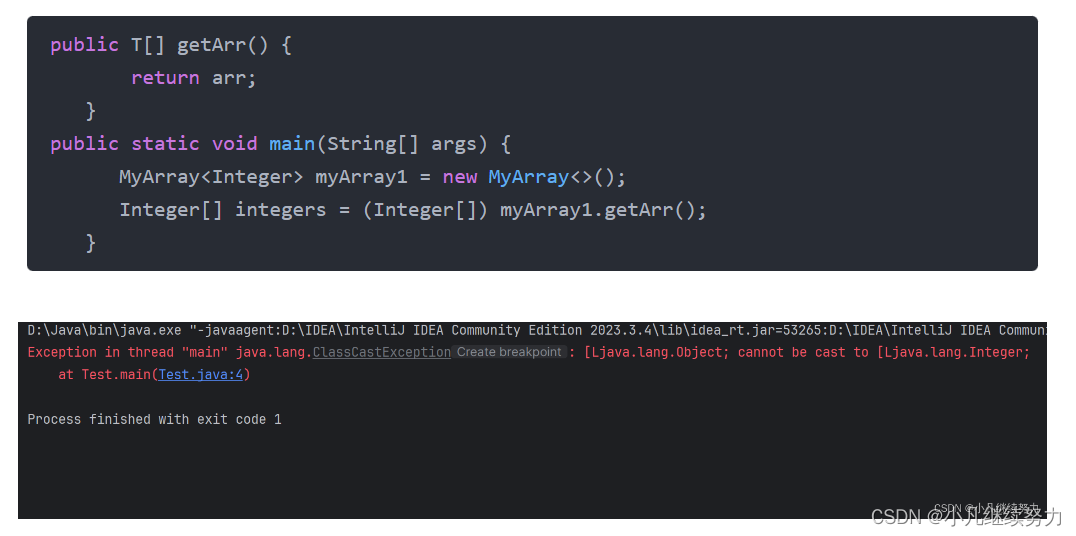
给一个方法就可以测试出
public T[] getArr() {return arr;}public static void main(String[] args) {MyArray<Integer> myArray1 = new MyArray<>();Integer[] integers = (Integer[]) myArray1.getArr();}4.2 泛型类的类型推导
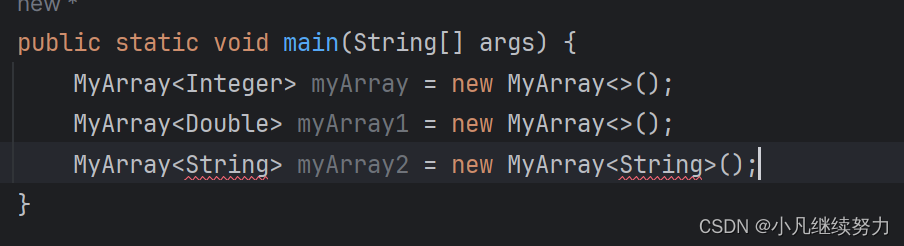
MyArray<Integer> list = new MyArray<>(); // 可以推导出实例化需要的类型实参为 Integer五、泛型是如何编译的
5.1 擦除机制
T[] array = new T[10];是不对的,编译的时候,替换为Object ,不是相当于:
Object[] array = new Object[10];
回到上文中的例子
六、泛型的上界
6.1 语法
class 泛型类名称<类型形参 extends 类型边界> {
...
}6.2 示例
class MyArray<T extends Number>{Object[] array = new Object[10];public void setArray(int pos,T val){this.array[pos] = val;}public T getVal(int pos){return (T)this.array[pos];//把返回的类强转为指定的类}
}表示指定的类是 Number 类或 Number 类的子类
6.3 复杂示例
要求写一个泛型类,求一个数组的最大值
public class Alg<T> {public T FindMaxVal(T[] arr) {T max = arr[0];for (int i = 1; i < arr.length; i++) {if (arr[i] > max) {max = arr[i];}}return max;}
}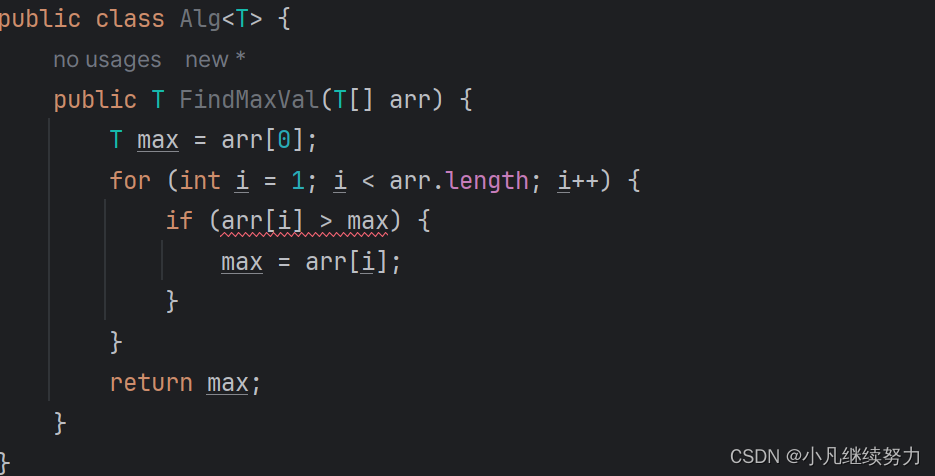
T 一定是引用数据类型,最终被擦除为了 Object 类型
而 Object 类型是没有是有 Comparable 接口的
不能进行比较,所以这里报错了
那在这里就需要将 T 约束实现了 Comparable 接口的
public class Alg<T extends Comparable<T>> {public T FindMaxVal(T[] arr) {T max = arr[0];for (int i = 1; i < arr.length; i++) {if (arr[i] > max) {max = arr[i];}}return max;}
}这里就表述传入的类型 T 一定是实现了 Comparable 接口的
那么实现了 Comparable 接口
就一定可以使用 CompareTo 方法
public class Alg<T extends Comparable<T>> {public T FindMaxVal(T[] arr) {T max = arr[0];for (int i = 1; i < arr.length; i++) {if (max.compareTo(arr[i]) < 0) {max = arr[i];}}return max;}
}这样就可以了
public class Main {public static void main(String[] args) {Alg<Integer> alg = new Alg<>();Integer[] integers = {1,2,3,4,5};System.out.println(alg.FindMaxVal(integers));}
}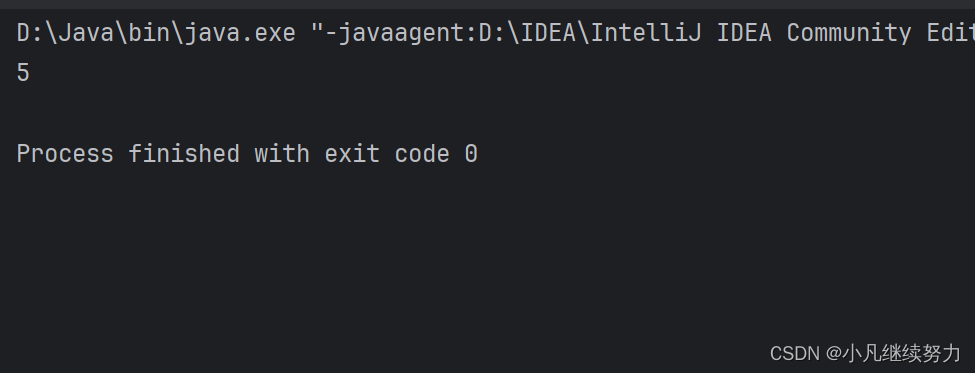
测试出来也是可以
也可以检测出没有实现 Comparable 接口的类
public class Person {public int age;public Person(int age) {this.age = age;}
}
public static void main(String[] args) {Person[] people = new Person[]{new Person(1), new Person(2), new Person(3)};Alg<Person> alg1 = new Alg<Person>();}
6.4 泛型方法
方法限定符 <类型形参列表> 返回值类型 方法名称(形参列表) { ... }上述是将指定类型放在类上
也可以将指定类型放在方法上
public class Alg{public <T extends Comparable<T>> T FindMaxVal(T[] arr) {T max = arr[0];for (int i = 1; i < arr.length; i++) {if (max.compareTo(arr[i]) < 0) {max = arr[i];}}return max;}
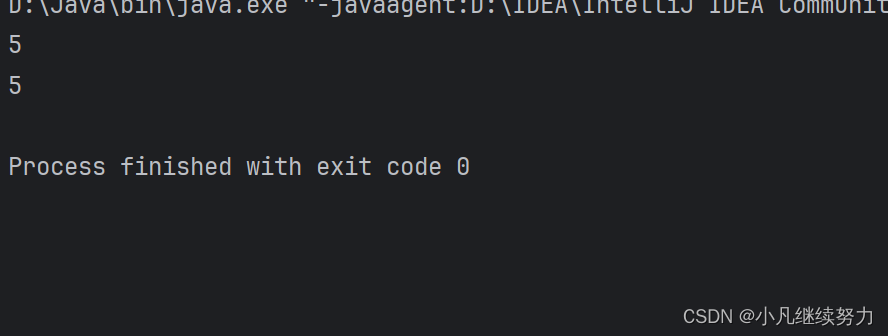
} public static void main(String[] args) {Alg alg = new Alg();Integer[] integers = {1, 2, 3, 4, 5};System.out.println(alg.FindMaxVal(integers));System.out.println(alg.<Integer>FindMaxVal(integers));}在实例化出来的 alg 调用 FindMaxVal 方法时
可以手动指定
也可以让编译器自己进行类型推导
如果不想实例化对象
可以将他写成一个静态方法
public static <T extends Comparable<T>> T FindMaxVal(T[] arr) {T max = arr[0];for (int i = 1; i < arr.length; i++) {if (max.compareTo(arr[i]) < 0) {max = arr[i];}}return max;}public static void main(String[] args) {Integer[] integers = {1, 2, 3, 4, 5};System.out.println(Alg.FindMaxVal(integers));System.out.println(Alg.<Integer>FindMaxVal(integers));}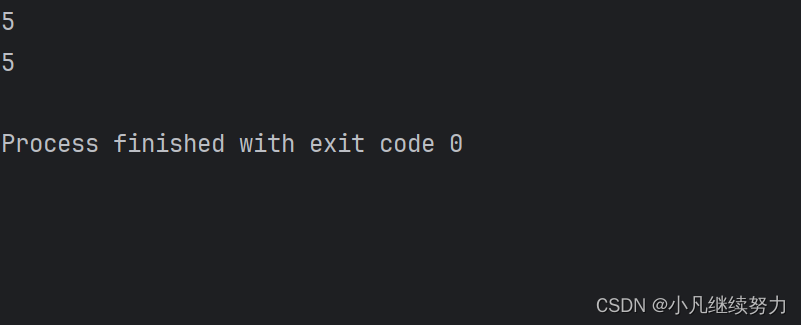
本文只是简述
谢谢观看

















