1.题目解析
题目来源:467.环绕字符串中唯一的子字符串
测试用例

2.算法原理
1.状态表示
首先创建一个和字符串大小相同的dp表,dp[i]表示以第i个位置的字符为结尾的所有字符串中在base中出现的次数,也就是以第i个位置的字符为结尾的所以子字符串在base中出现的次数
2.状态转移方程
根据题目我们知道如果两个字符连续就代表可以构成字符串并且在base中出现,并且base是无限循环的,因此za也是一个在base中出现的字符串,此时可以得出下列的状态转移方程
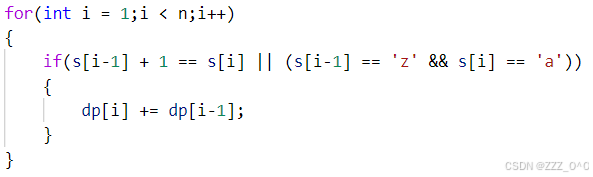
3.初始化
由于base中出现了所有的小写字母,因此单个字符一定出现在base中,所以给dp表的每一个位置都初始化为1就不用单独去判断单个字符的情况
4.填表顺序
从左到右
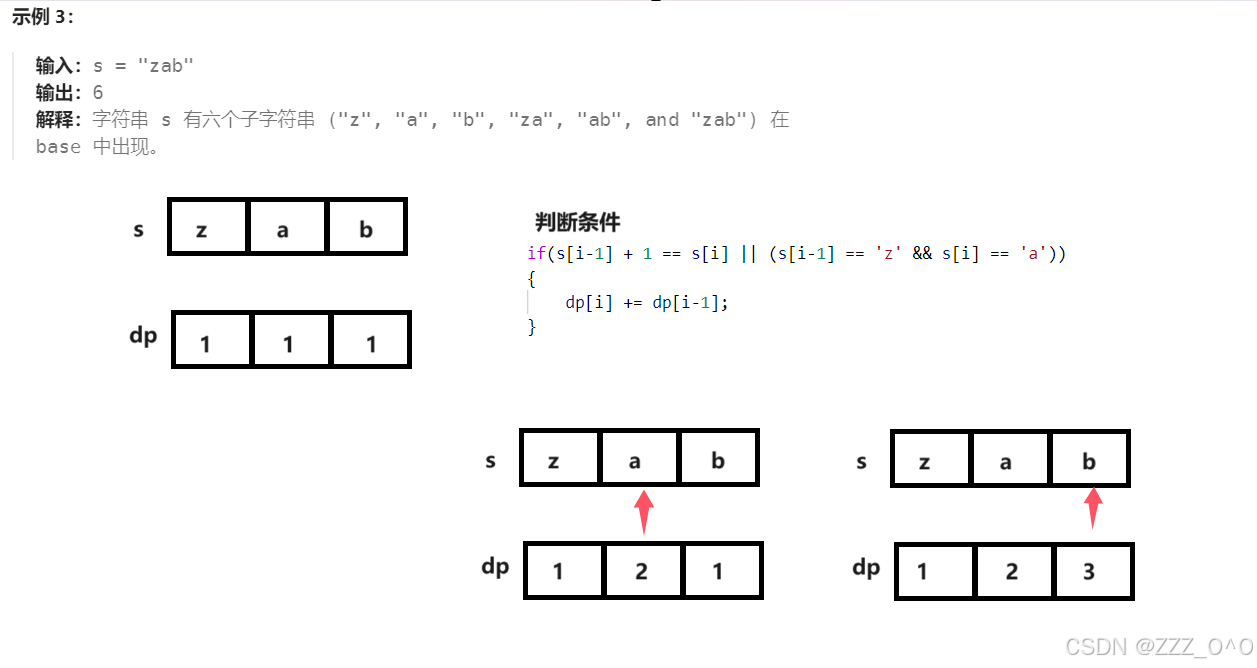
5.返回值
这里不能直接返回dp表所有元素之和,因为需要去重,比如以相同的字母结尾那么短的字符串一定包含于长的字符串之内,这时只需要计算长的字符串中子字符串在base中出现的次数即可,不用重复统计短的字符串出现的次数,因此创建一个数组代替哈希表,每个位置对应的就是以不同字符结尾的子字符串在base中出现的次数,最后将哈希表的所有值相加即可
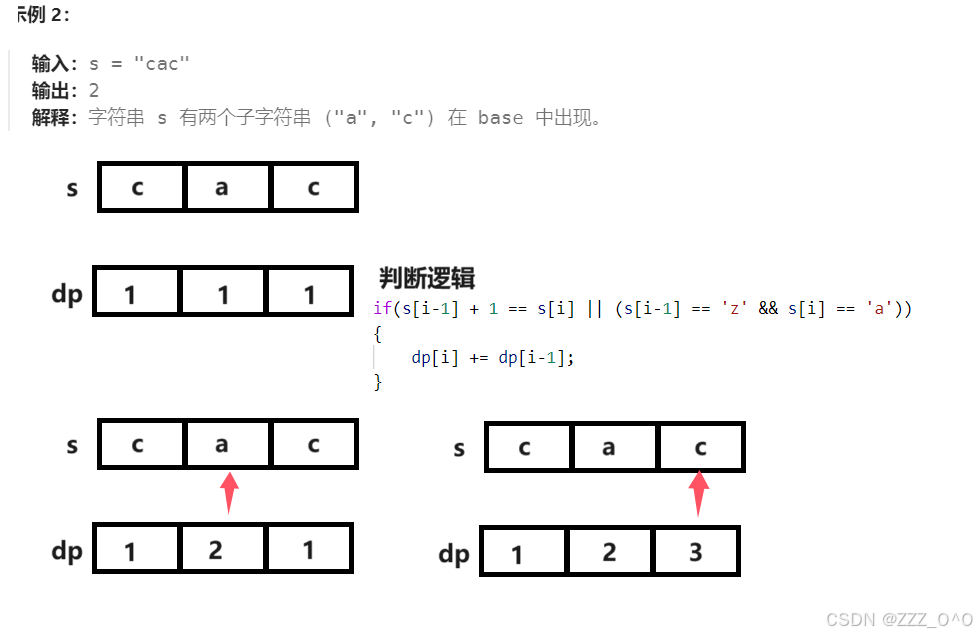
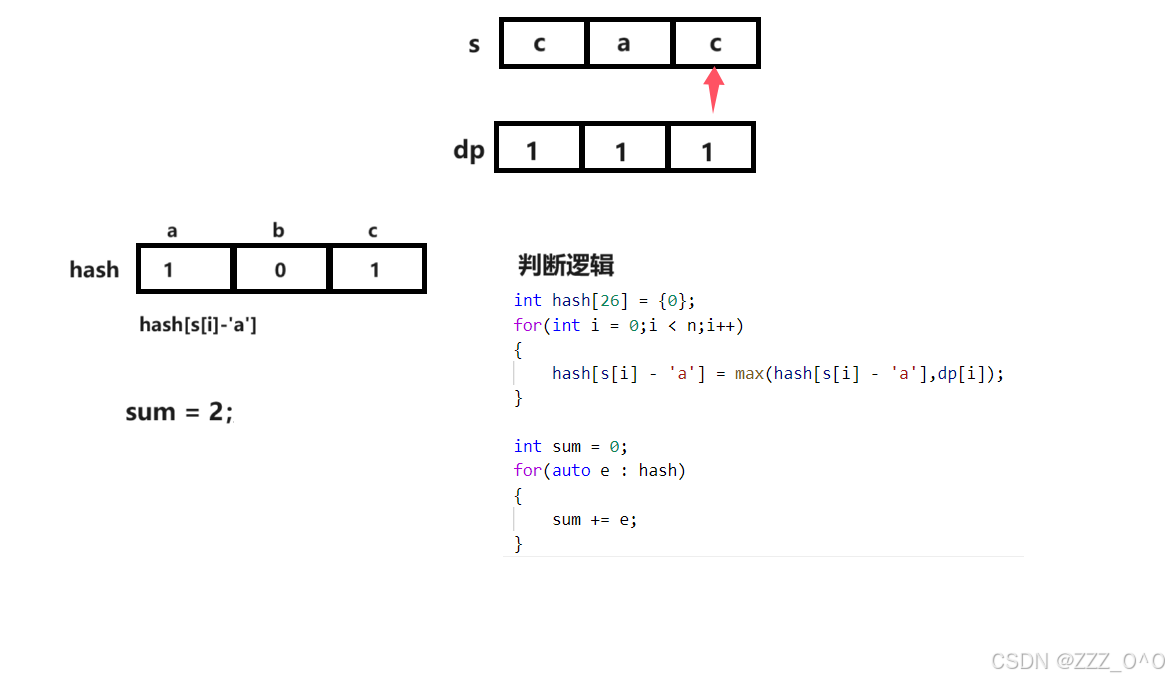
3.实战代码
class Solution {
public:int findSubstringInWraproundString(string s) {int n = s.size();vector<int> dp(n,1);for(int i = 1;i < n;i++){if(s[i-1] + 1 == s[i] || (s[i-1] == 'z' && s[i] == 'a')){dp[i] += dp[i-1];}}int hash[26] = {0};for(int i = 0;i < n;i++){hash[s[i] - 'a'] = max(hash[s[i] - 'a'],dp[i]);} int sum = 0;for(auto e : hash){sum += e;}return sum;}
};














