
摘要
本文提出了一种改进的灰狼算法——非线性自适应分组灰狼算法(Nonlinear Adaptive Grouped Grey Wolf Optimizer, NAGGWO),用于解决多峰函数优化问题。该算法通过引入自适应分组策略和非线性权重更新机制,使得灰狼群体在搜索过程中的探索和开发能力得到平衡。实验结果表明,NAGGWO在多个标准测试函数上表现出优越的收敛速度和全局搜索能力。
理论
灰狼优化算法(Grey Wolf Optimizer, GWO)模拟灰狼的捕猎行为,主要包括追踪、包围和攻击猎物。传统GWO在优化过程中可能容易陷入局部最优,因此本文引入了自适应分组策略,即在优化过程中将灰狼群体分为多个子群,每个子群负责不同的搜索任务。同时,使用非线性权重更新机制,逐步提高群体的开发能力,使算法更容易跳出局部最优。
实验结果
在基准函数测试中,NAGGWO与其他优化算法(如GWO、SSA、HHO)进行了对比。以下是部分基准函数上的实验结果:
-
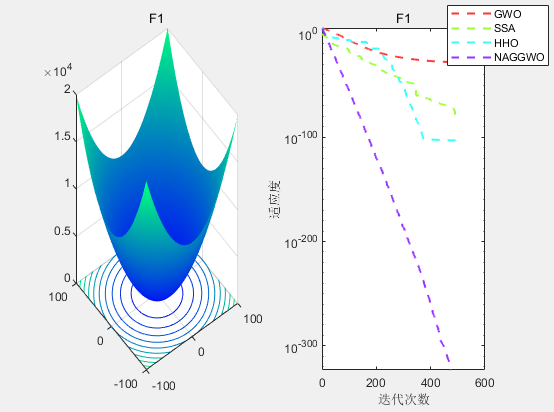
F1函数:如图1所示,左侧为F1函数的三维形状,右侧为各算法的收敛曲线。NAGGWO的收敛速度明显快于其他算法。
-
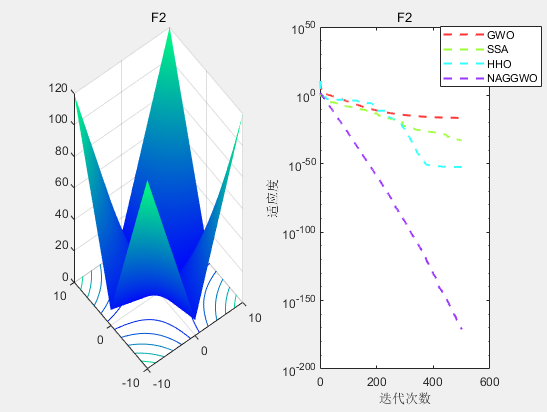
F2函数:如图2所示,NAGGWO在F2函数上的优化效果依旧优于其他算法。
-
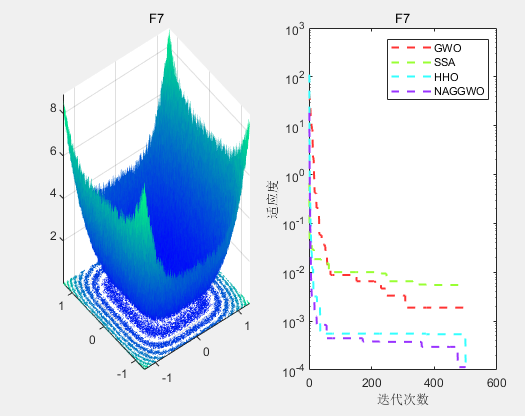
F7函数:如图3所示,NAGGWO在F7函数上实现了更好的全局最优搜索性能,表现出更强的鲁棒性。
部分代码
% 初始化参数
numWolves = 30; % 灰狼数量
maxIter = 500; % 最大迭代次数
dim = 2; % 变量维度
bounds = [-100, 100]; % 变量范围% 初始化灰狼位置
positions = bounds(1) + (bounds(2) - bounds(1)) * rand(numWolves, dim);% 迭代优化过程
for iter = 1:maxIter% 计算适应度值fitness = evaluateFitness(positions);% 按适应度值排序并分组[sortedFitness, index] = sort(fitness);positions = positions(index, :);% 更新Alpha、Beta和Delta位置alpha = positions(1, :);beta = positions(2, :);delta = positions(3, :);% 更新位置(非线性自适应分组策略)for i = 4:numWolvesA = 2 * (1 - iter / maxIter) * rand(1, dim) - 1;C = 2 * rand(1, dim);positions(i, :) = updatePosition(alpha, beta, delta, positions(i, :), A, C, bounds);end
end% 绘制收敛曲线
plotConvergence(sortedFitness);
参考文献
❝
Mirjalili, S., & Lewis, A. (2014). Grey Wolf Optimizer. Advances in Engineering Software, 69, 46-61.
Zhang, J., & Xie, W. (2020). Adaptive Grey Wolf Optimizer for Solving Complex Optimization Problems. Applied Soft Computing, 87, 106011.
Wang, L., & Zhou, W. (2021). Nonlinear Adaptive Mechanisms in Swarm Intelligence Algorithms. IEEE Transactions on Evolutionary Computation, 25(3), 565-580.
(文章内容仅供参考,具体效果以图片为准)












)

