谈谈高斯核
早期是这样的


历史已经成为历史了,现在的浮点运算早已经不是问题了。有的人总是活在上个世纪。
现在是对二维高斯函数关于中心采样来获取任意尺寸的高斯平滑模板。

关于模板的尺寸

ceil 函数表示向上取整操作,即不小于x的最小整数。
floor函数表示向下取整操作,即不大于x的最大整数。
冈萨雷斯是错误的,这个也不是奇数,显而易见的错误。

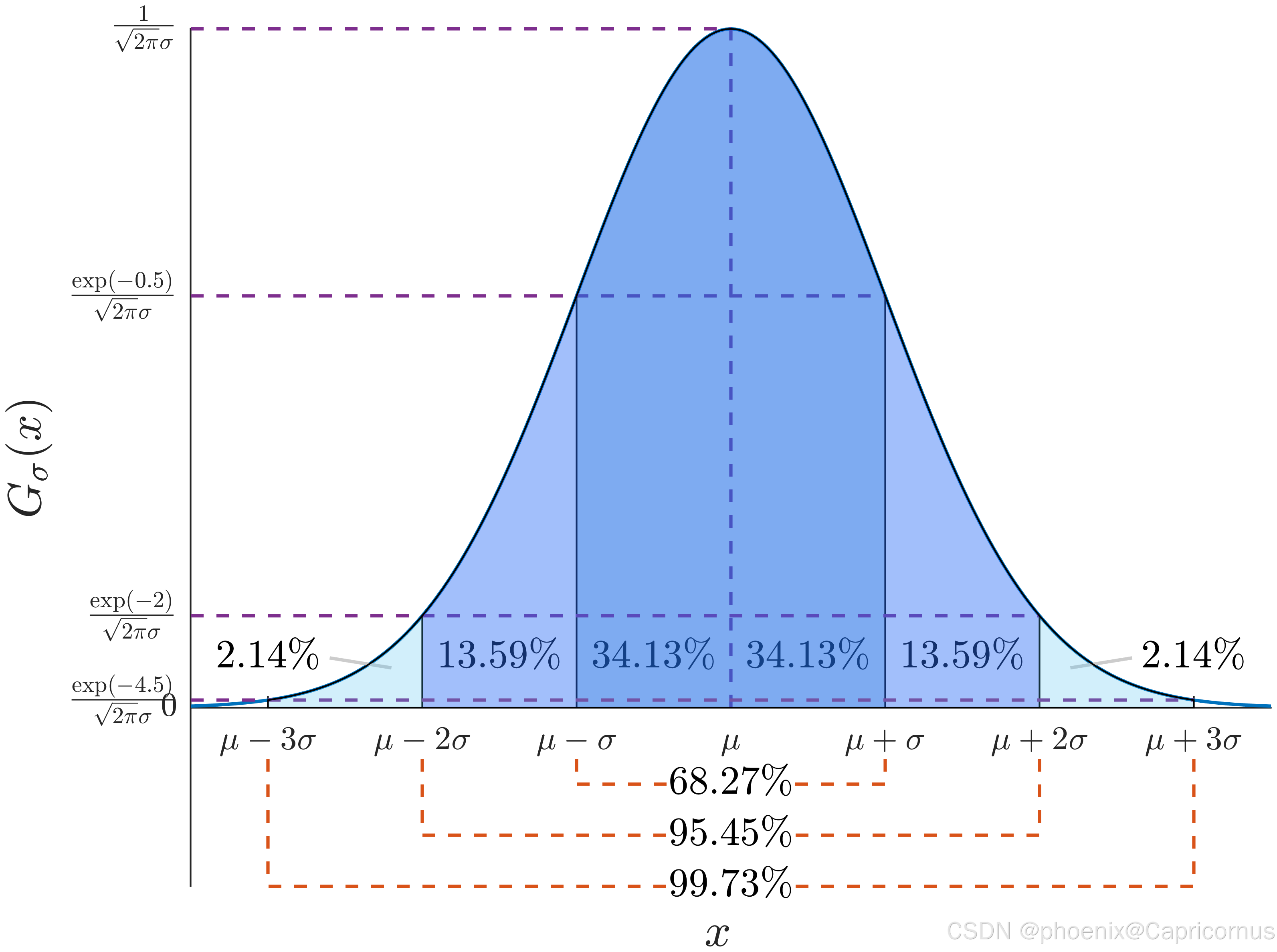
给出 2 σ 2\sigma 2σ的几个不同尺寸的高斯核。
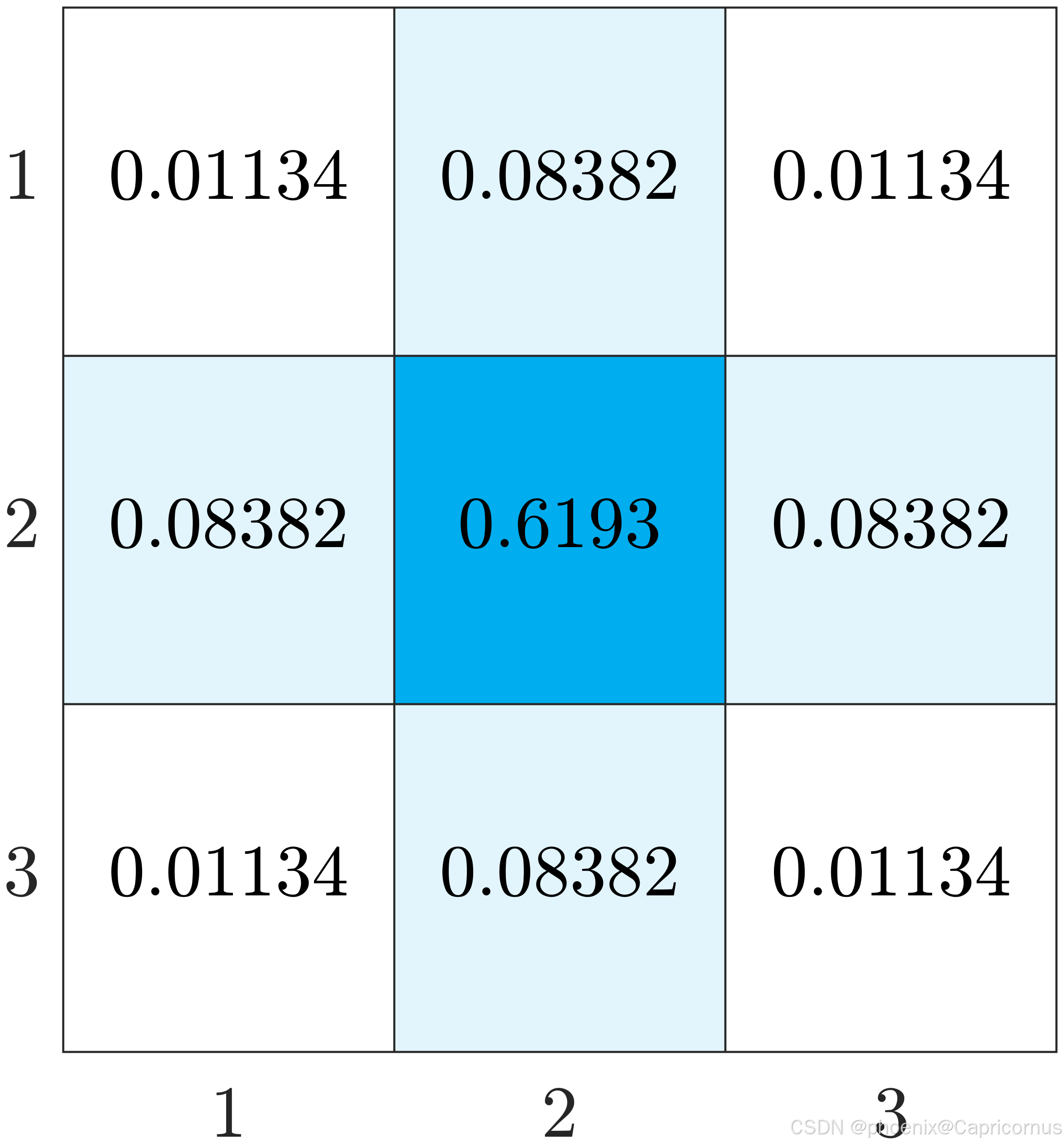
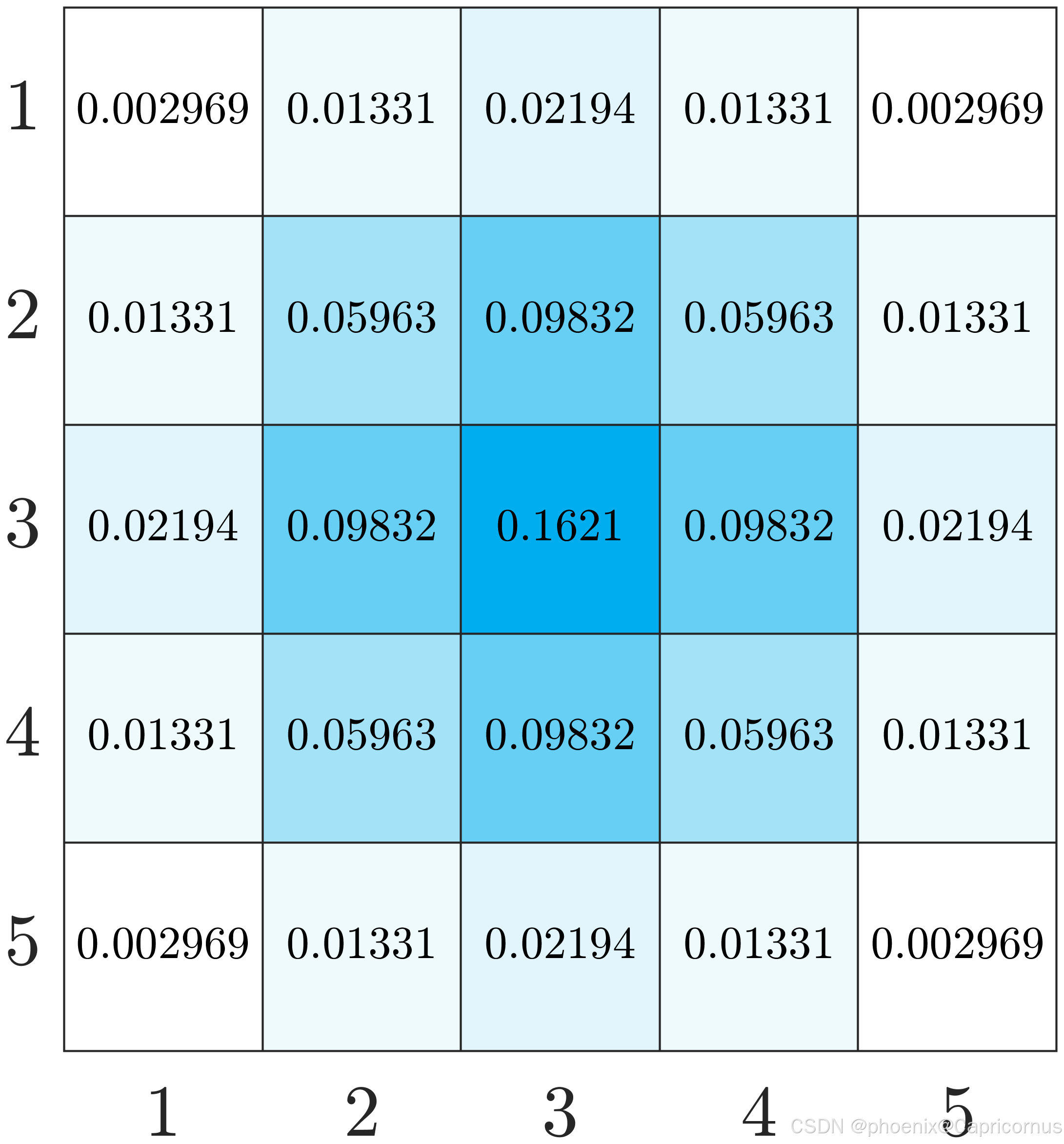
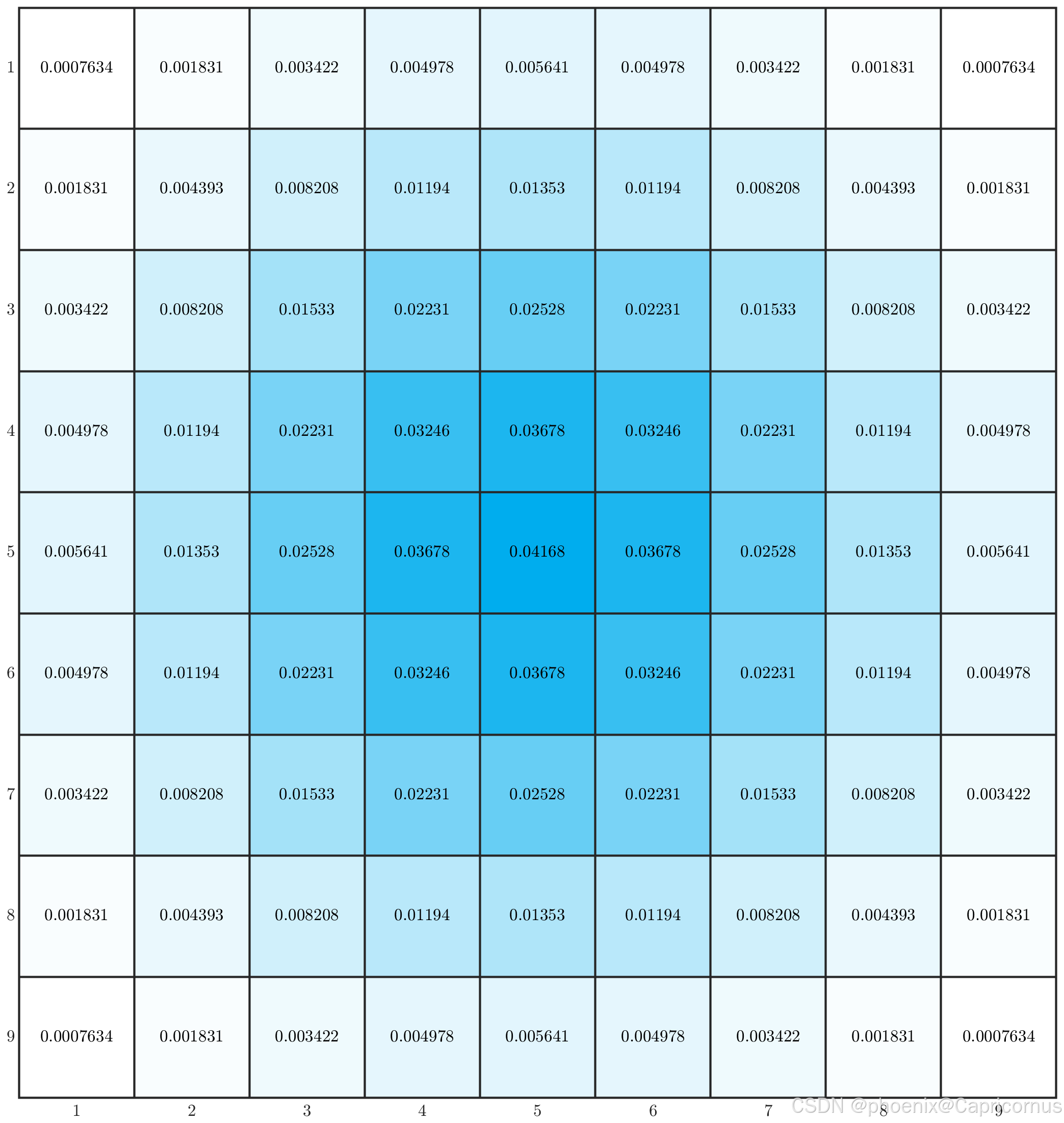
禹晶、肖创柏、廖庆敏《数字图像处理(面向新工科的电工电子信息基础课程系列教材)》
在早期的数字信号处理和图像处理等领域中,因为计算能力和存储资源的限制,模板(或称为卷积核、滤波器等)的系数通常设计为整数。
-
计算效率:整数运算比浮点运算更高效。早期的处理器在执行浮点运算时速度较慢,且消耗更多的计算资源。使用整数可以显著提高算法的运行速度。
-
存储效率:整数相比浮点数占用更少的存储空间。在早期计算机系统中,内存和存储资源都非常有限,因此使用整数可以节省宝贵的存储资源。
-
硬件支持:早期的很多计算机系统缺乏对浮点运算的硬件支持,或者浮点运算单元(FPU)的性能较低。使用整数可以避免这些硬件上的限制。
-
简化设计:整数运算相对简单,易于实现和调试。在嵌入式系统和实时处理系统中,简化设计可以降低开发成本和复杂度。
-
减少误差:在某些情况下,使用整数可以减少由于浮点运算带来的累积误差问题。虽然这一点在现代计算环境中已经不那么重要,但在早期是一个需要考虑的因素。
然而,随着计算技术的发展,现代计算机系统在计算能力和存储资源上有了显著提升,浮点运算已经成为标准配置。因此,现代的数字信号处理、图像处理和其他应用中,模板系数不再局限于整数,而是可以根据具体需求选择最合适的数值类型,包括浮点数,以获得更高的精度和灵活性。例如,在深度学习和计算机视觉等领域,使用浮点数可以提供更精细的控制和更好的处理效果。
廖老师常给我讲历史,我说历史已经是历史了,我感觉他在忆苦,让我思甜。不管怎么样,他喜欢讲,我就听着。
科学技术是第一生产力。科技发展很快,不努力就会被时代淘汰,更别提停滞不前、固步自封。被时代淘汰,时代都不会提前打招呼,连个心理准备的时间都不给留,常常是反应过来的时间,时代都变了。














