数据结构入门学习（全是干货）——树（上）

1 树与树的表示

什么是树？

树是一种层次型的组织结构，常见于人类社会的家谱、公司组织结构、图书信息管理等。树结构在数据管理，特别是查找（Searching）操作上具有更高的效率。

树的用途：

1. 家谱、社会组织结构：展示各层次关系。
2. 图书信息管理：帮助查找和组织数据。

---

1.1 引子：查找（Searching）

查找：根据某个给定关键字K，从集合R中找出关键字与K相同的记录静态查找：集合中记录是固定的没有插入和删除操作，只有查找(例如查字典)动态查找：集合中记录是动态变化的除查找，还可能发生插入和删除

静态查找：

方法1：顺序查找（Sequential Search）
顺序查找是一种最简单的查找方式，适用于无序数据的线性表。

int SequentialSearch (List Tbl,ElementType K)
{//	在Element[1]~Element[n]中查找关键字为K的数据元素int i;Tbl->ElementP[0] = K;//建立哨兵for(i = Tbl->Length;Tbl->Element[i] != K;i--);//倒过来做的，从下标大的地方开始往前循环return i;//查找成功返回所在单元下标;不成功不返回0
}typedef struct LNode{ElementType Element[MAXSIZE];//决定了放的元素有多少个int Length;
};顺序查找的一种实现(无"哨兵")int SequentialSearch (List Tbl ,ElementType K)
{//在Element[1]~Element[n]中查找关键字为K的数据元素int i;for(i=Tbl->Length; i>0 && Tbl->Element[i] != K;i--);return i;//查找成功返回所在单元下标，不成功返回0
}
在顺序查找中,如果把下列程序中的循环条件"i>0"去掉，会发生什么后果？答案：要查找的元素不存在时发生数组越界（i指向小于0的位置）"哨兵"的作用:可以在数组的最后或者边界上面设一个值，不用每次去判断它的下标是不是达到我的边界。根据for循环，当碰到我们放置的那个值的时候，循环就该退出来了。这样我们在写判断的时候就可以少写一个判断的分支我的理解是这个哨兵通常放置在下标0的地方，然后循环从大往小循环，循环到1如果都没有我们需要的值的时候，放在下标0的地方的哨兵是等于我们需要的值来退出循环，代替了for条件中的不能小于0，防止for循环陷入死循环或者说越界跑到下标负数的地方去了。然后返回值如果是0的话我们就心知肚明没有找到我们想要的值了这种顺序查找算法的时间复杂度为O(n)，平均数是n/2

---

1.2 引子：二分查找（Binary Search）

方法2：二分查找
二分查找是一种高效的查找方法，前提是数据必须有序。二分查找通过每次将查找范围减半来实现查找，时间复杂度为 O(log⁡N)

例子1：假设有13个数据元素，按关键字从小到大顺序存放，使用二分查找关键字为 444 的数据过程如下：

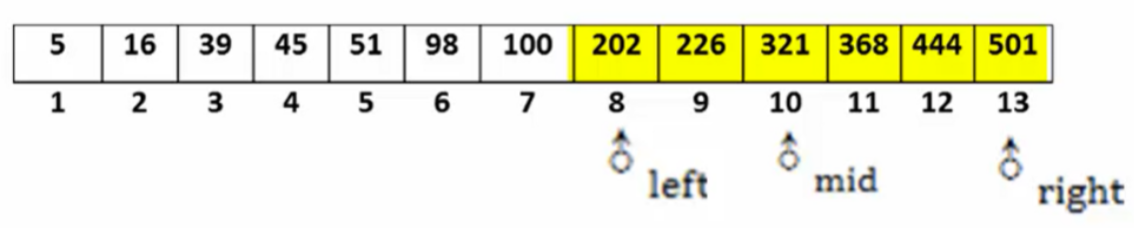
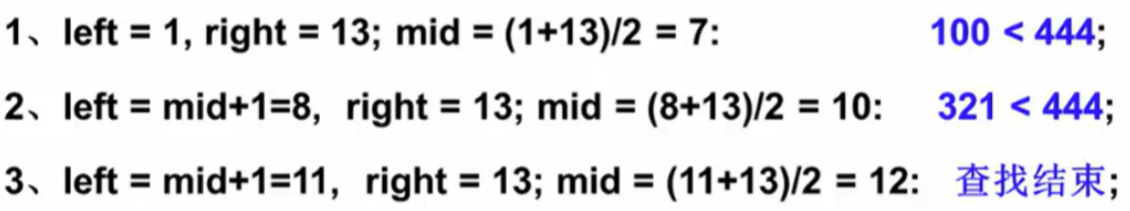
• 首先查找中间元素，如果不匹配，则继续在较大或较小的一半中查找，直到找到关键字或查找范围为空。

例子2：二分查找关键字为 43 的过程类似，逐步缩小查找范围。

---

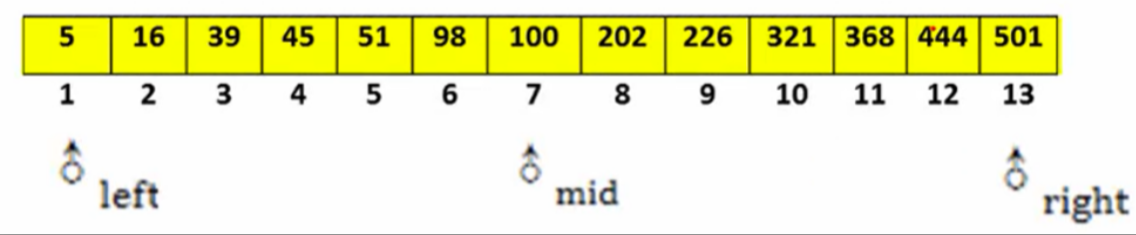
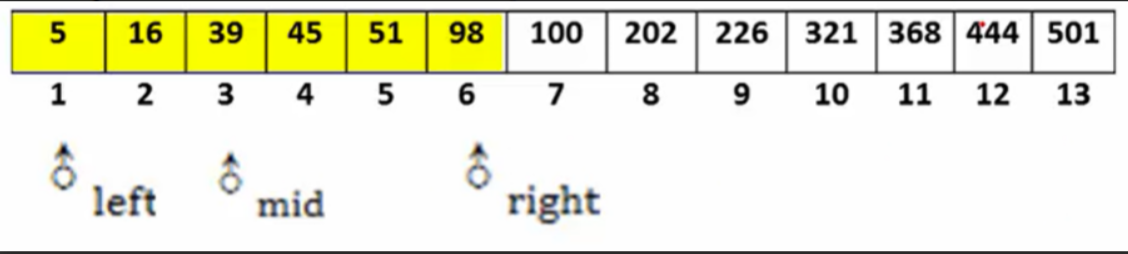
1.3 引子：二分查找实现

二分查找算法

• 二分查找算法的时间复杂度为 O(log⁡N)O(\log N)O(logN)，对于有序数据的查找效率非常高。

int BinarySearch(List Tbl,ElementType K)//List Tbl是结构的指针，包含了数组Element和它的大小Length
{//在表Tbl中查找关键字为K的数据元素int left,right,mid,NoFound = -1;left = 1;//初始左边界right = Tbl->Length//初始右边界while(left <= right){mid = (left + right)/2 //计算中间元素坐标if(K < Tbl->Element[mid])   right = mid - 1;//调整右边界else if(K > Tbl->Element[mid]) left = mid + 1;//调整左边界else return mid;//查找成功，返回数据元素下标}return NotFound;//查找不成功，返回-1
}
所以我们就return NotFound在二分查找的程序实现中，如果left和right的更新不是取mid+1和mid-1而是都取mid，程序也是正确的?当然是错误的啦//List定义: List是stl实现的双向链表,与向量(vectors)相比, 它允许快速的插入和删除,但是随机访问却比较慢。使用时需要添加头文件 #include

判定树

• 二分查找的过程可以用判定树表示，判定树的每个节点代表一次查找操作。
• 深度：判定树的深度就是查找需要的最大次数。
• 平均成功查找次数（ASL）：可以通过对所有查找次数取平均值来计算。

---

1.4 树的定义和术语

树的定义：

树（Tree） 是 n 个节点构成的有限集合。当 n=0 时，称为空树。当 n>0 时，树具有以下性质：

1. 树中有一个称为“根（Root）”的特殊节点，记为 r。
2. 除根节点外，树的其余节点可以分为若干不相交的子树，每个子树也是一棵树。

树的性质：

• 树的节点之间通过边相连，一棵树有 n−1 条边。
• 树是保持节点之间连通的最小连接方式。

---

树的一些基本术语

1. 节点的度（Degree）：节点拥有的子树的个数。
2. 树的度：树中所有节点的最大度数。
3. 叶节点（Leaf）：度为 0 的节点。
4. 父节点（Parent）：有子树的节点称为子树根节点的父节点。
5. 子节点（Child）：若节点 A 是节点 B 的父节点，则称 B 是 A 的子节点。
6. 兄弟节点（Sibling）：具有相同父节点的各节点称为兄弟节点。
7. 祖先节点（Ancestor）：从根节点到某一节点路径上的所有节点称为该节点的祖先。
8. 子孙节点（Descendant）：某节点的所有子树中的节点称为该节点的子孙。
9. 节点的层次（Level）：根节点的层次为 1，其他节点的层次是其父节点层次加 1。
10. 树的深度（Depth）：树中所有节点的最大层次称为树的深度。

---

1.5 树的表示方法

数组实现：

树的节点可以顺序存储在数组中，但每个节点的度可能不同，数组的静态表示会造成存储空间的浪费。

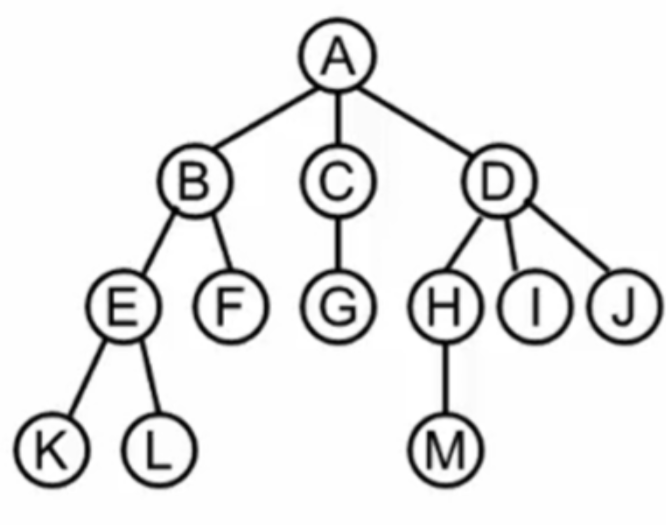
链表实现：

树的链表表示法根据节点的度数进行动态分配。每个节点包含若干指针域，指向其子节点。

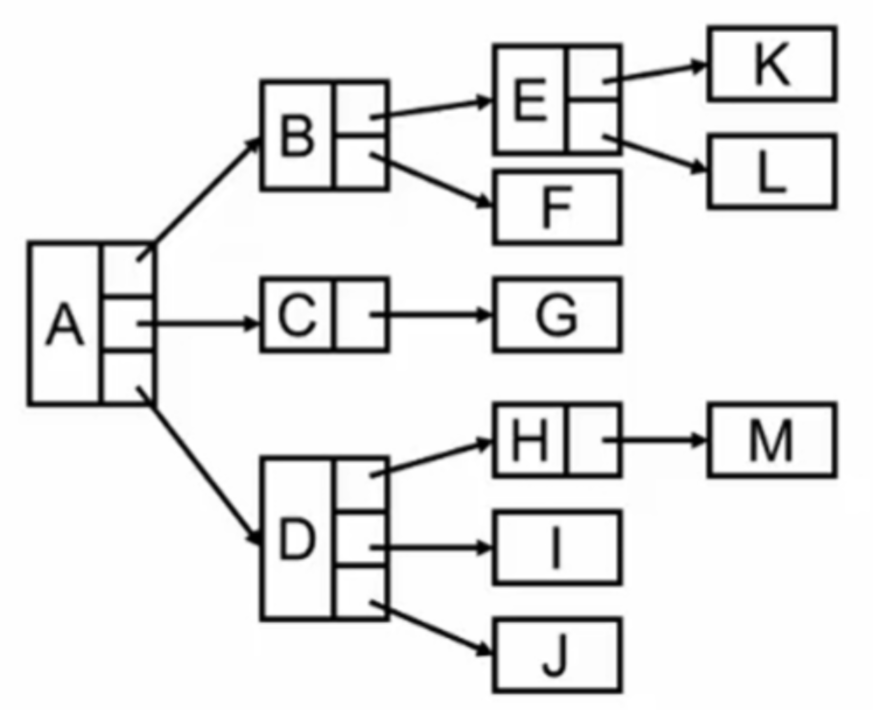
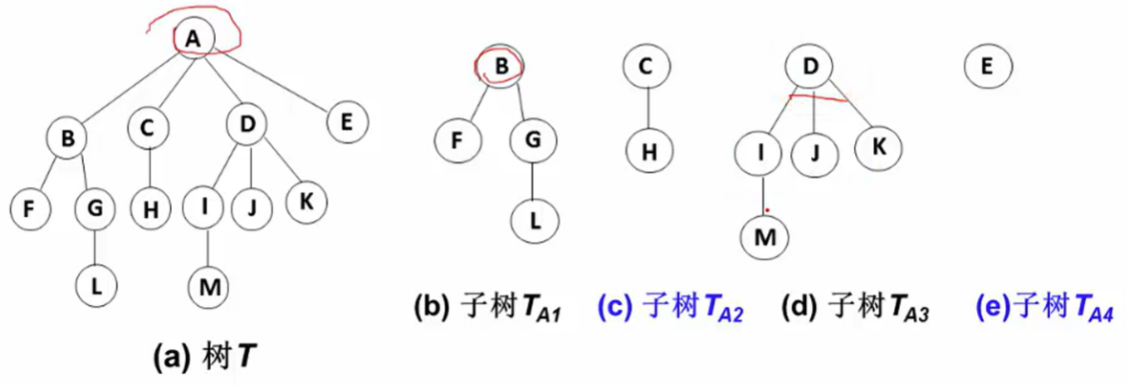
儿子-兄弟表示法：

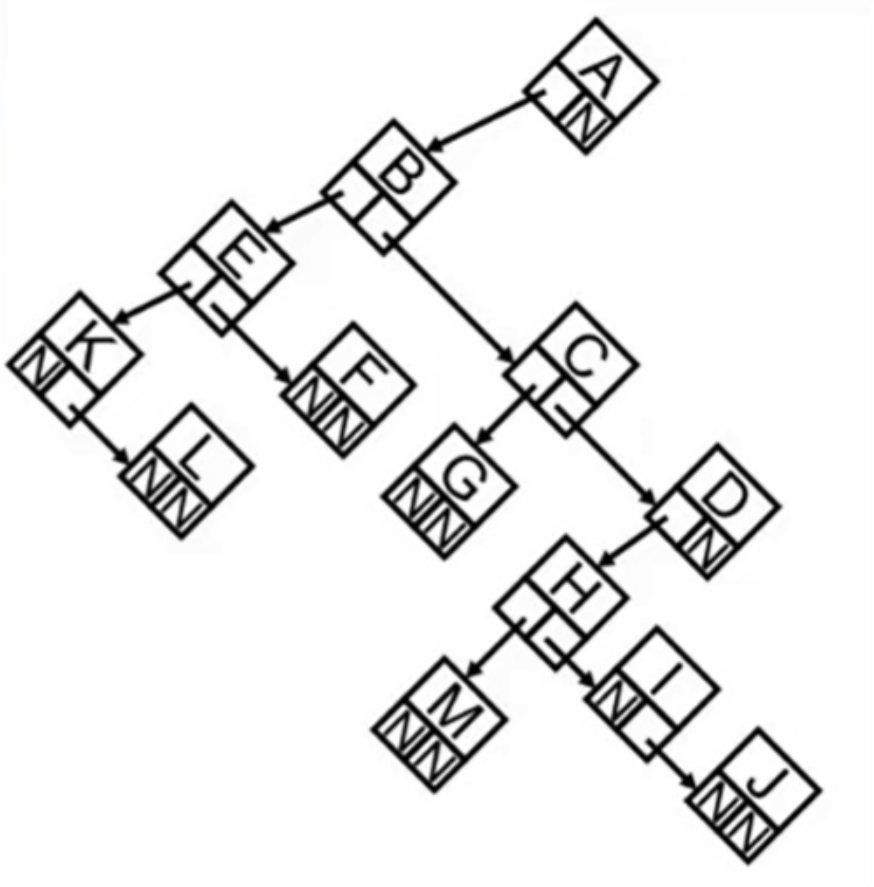
通过使用儿子-兄弟表示法，可以将树结构简化为二叉树的形式。每个节点的第一个孩子通过左指针指向，其他兄弟节点通过右指针链接。

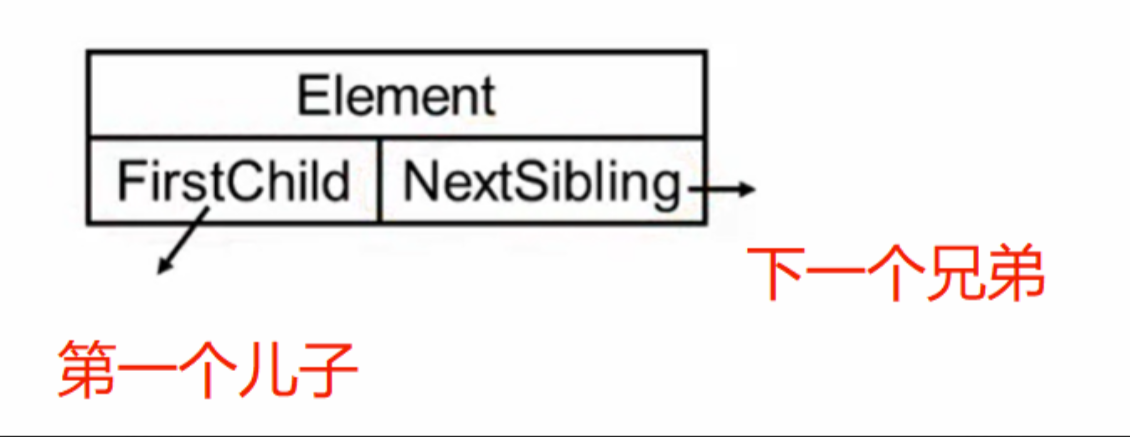
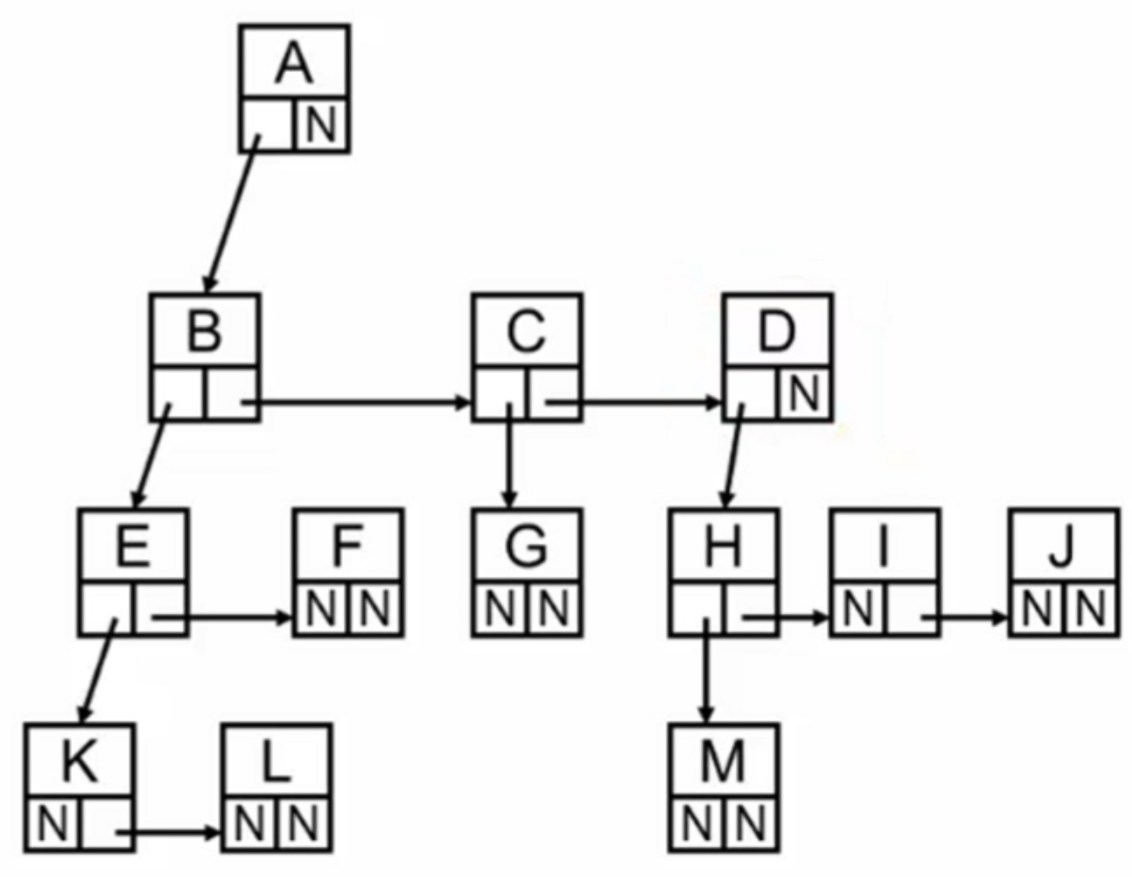
这种方法的优点:
1.树种的每个结点结构都是统一的，都是两个指针域，同时它的空间浪费也不大n个结点2n个指针域 其中n-1条边。意味着n-1个域是非空的，真正空的域是n+1问题：在用“儿子-兄弟”法表示的树中，如果从根结点开始访问其“次子”的“次子”，所经过的结点数与下面哪种情况一样？(注意:比较的是结点数,而不是路径)答案：从根结点开始访问其“长子”的“长子”的“长子”的“长子”

---

2.1 二叉树的定义及性质

二叉树的定义：

二叉树（Binary Tree） 是度不超过 2 的树，即每个节点最多有两个子节点，分别称为左子节点和右子节点。

二叉树的五种基本形态：

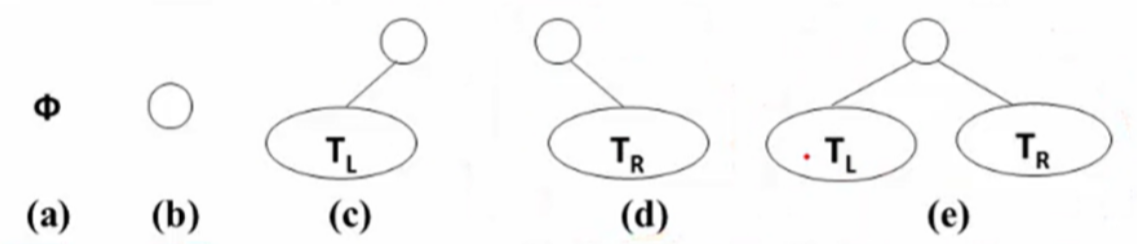
1. 空二叉树：不含任何节点的二叉树。
2. 只有根节点的二叉树。
3. 只有左子树的二叉树。
4. 只有右子树的二叉树。
5. 左右子树都有的二叉树。

---

特殊的二叉树

1. 斜二叉树（Skewed Binary Tree）：所有节点都只有左子树或右子树，相当于一个链表。

   

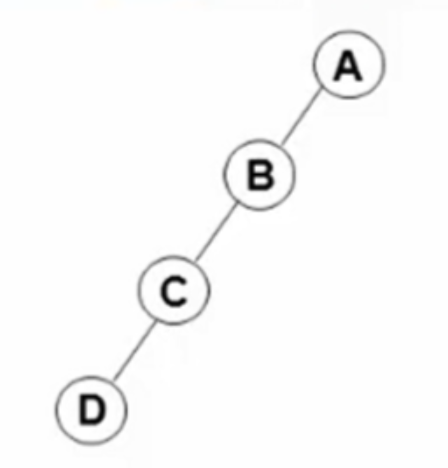
2. 完美二叉树（Perfect Binary Tree）：所有层的节点都满，节点数为 2^{k+1} - 1，其中 k 是树的深度。

   

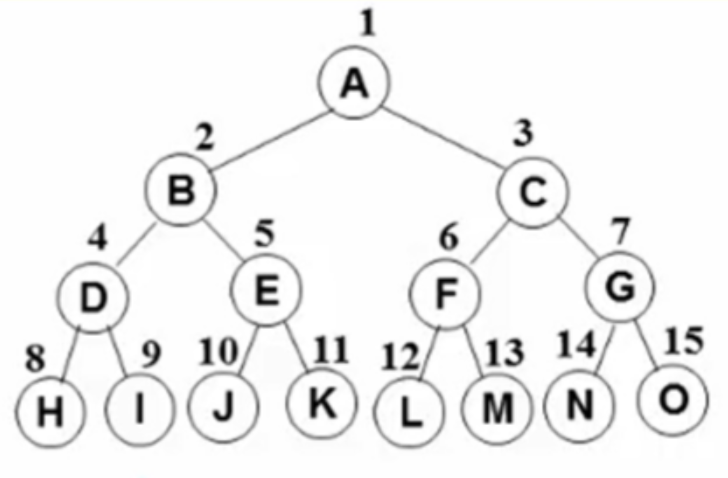
3. 完全二叉树（Complete Binary Tree）：除了最后一层，其他层的节点都是满的。

   有n个结点的二叉树，对树种结点按从上到下，从左到右的顺序进行编号，编号为i(1 <= i <= n)结点与满二叉树中编号为i结点在二叉树中位置相同
   跟上方的区别就是除了最底下一层可以右边缺一点，上面跟满二叉树是一样的。最底下一层左边顺序不能乱
   

二叉树的性质：

1. 二叉树的叶节点总数等于拥有两个子节点的节点总数加 1。

   

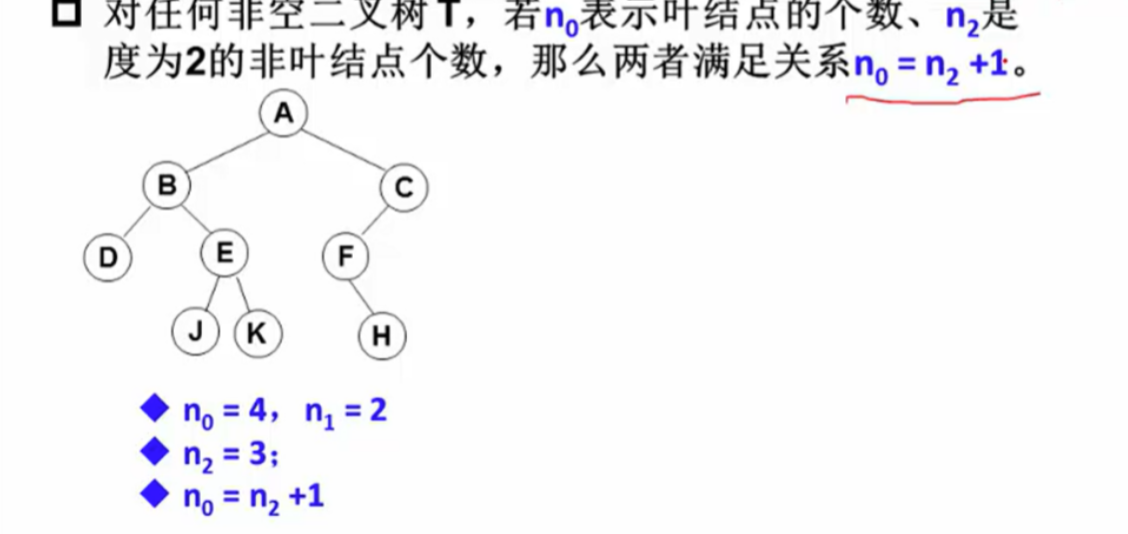
2. 二叉树可以通过先序、中序、后序等方式进行遍历。

---

2.2 二叉树的存储结构

1. 顺序存储结构：

   • 非根节点的父节点序号为 i / 2。
   • 节点 i 的左孩子序号为2i，右孩子序号为 2i+1。
   • 缺点：当树不满时，会浪费空间。

   

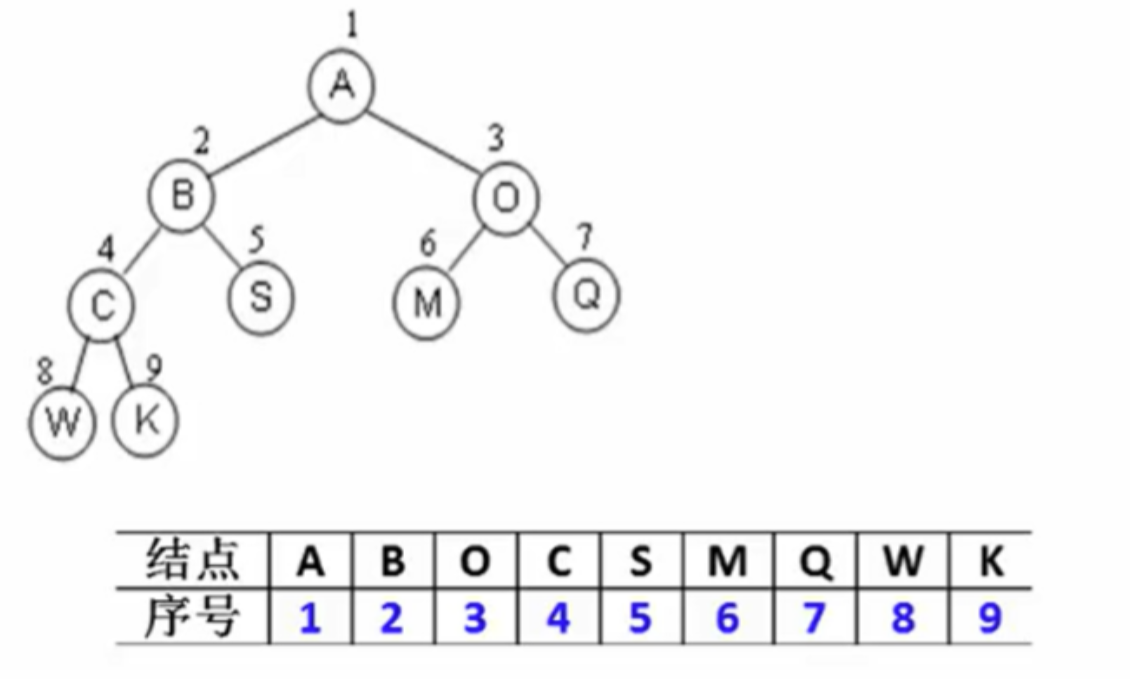
2. 链表存储结构：

3. 

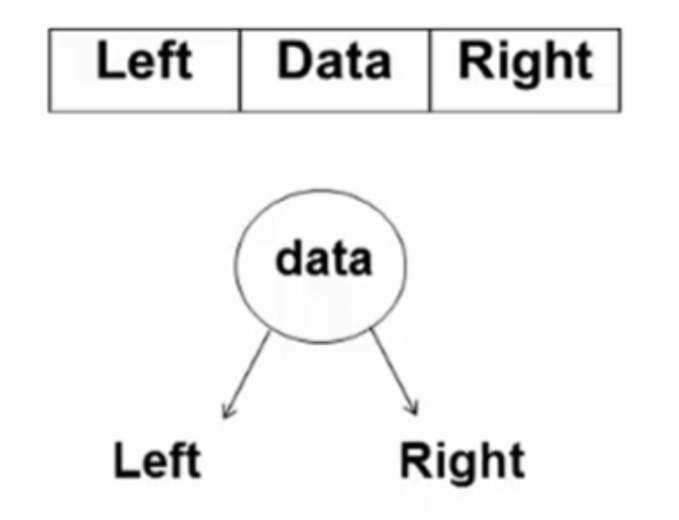
   • 每个节点包含指向左子树和右子树的两个指针。

   typedef struct TreeNode *BinTree;
   typedef BinTree Position;
   struct TreeNode{ElementType Data;BinTree Left;BinTree Right;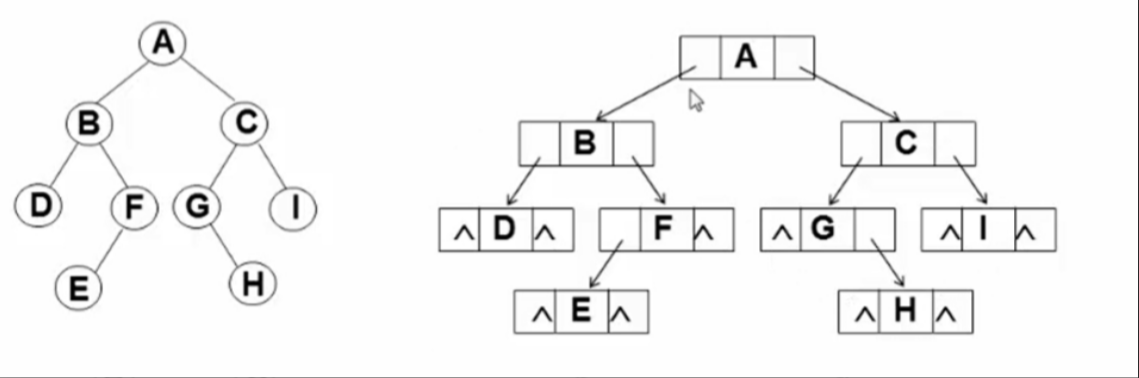
   }
   

   

---

3. 二叉树的遍历

二叉树的遍历是指按照某种规则访问二叉树中的每一个节点。常见的遍历方式有：

1. 先序遍历（Preorder Traversal）：先访问根节点，然后遍历左子树，最后遍历右子树。

   遍历过程为：
   1.访问根节点
   2.先序遍历其左子树
   3.先序遍历其右子树 对应的递归程序：
   void PreOrderTraversal(BinTree BT)//BT是树
   {if( BT ){//看树是不是空的，空的就退出去，不空就访问根节点printf("d",BT->Data);PreOrderTraversal(BT->Left);//指向左子树的那个根节点的地址进行递归PreOrderTraversal(BT->Right);//指向右子树的那个根节点的地址进行递归}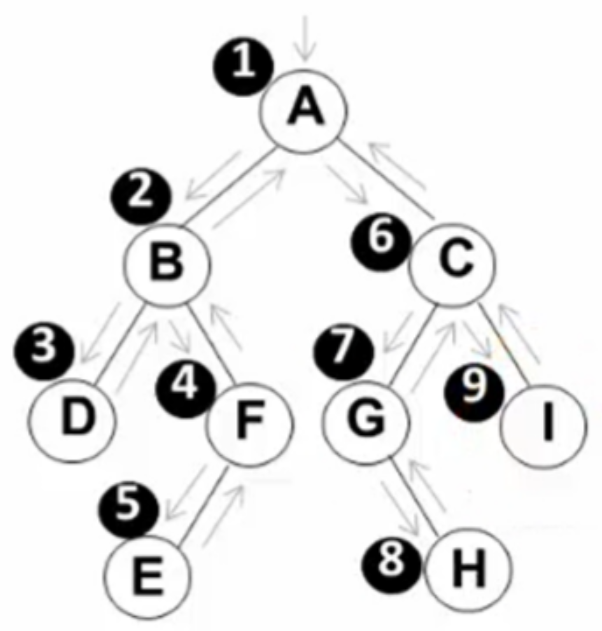
   }

   

   
   先是从根开始  A(B D F E)(C G H I)
   先序遍历=>A B D F E C G H I
   

2. 中序遍历（Inorder Traversal）：先遍历左子树，然后访问根节点，最后遍历右子树。

   遍历过程为：
   1.中序遍历其左子树
   2.访问根结点;
   3.中序遍历其右子树 
   对应的递归程序：
   void PreOrderTraversal(BinTree BT)//BT是树
   {if( BT ){//看树是不是空的，空的就退出去，不空就访问根节点PreOrderTraversal(BT->Left);//指向左子树的那个根节点的地址进行递归printf("d",BT->Data);PreOrderTraversal(BT->Right);//指向右子树的那个根节点的地址进行递归}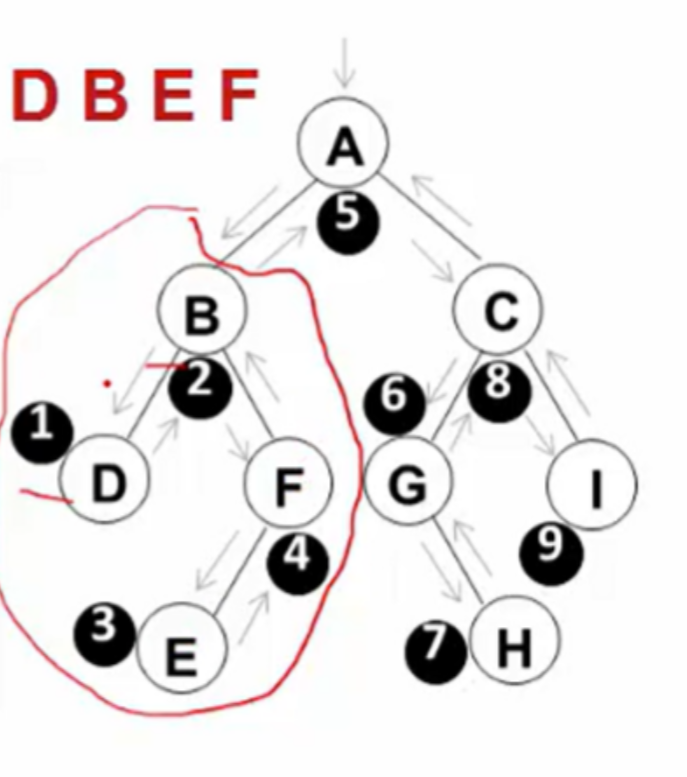
   }
   

   

   中序遍历 => D B E F A G H C I
   (D B E F) A ( G H C I)
   先是左边再右边，这里我原本的疑问是为什么是先E在F而不是先F再E
   原因是E-F是一个树，然后因为这个是左子树，所以从左边开始，E在F的左边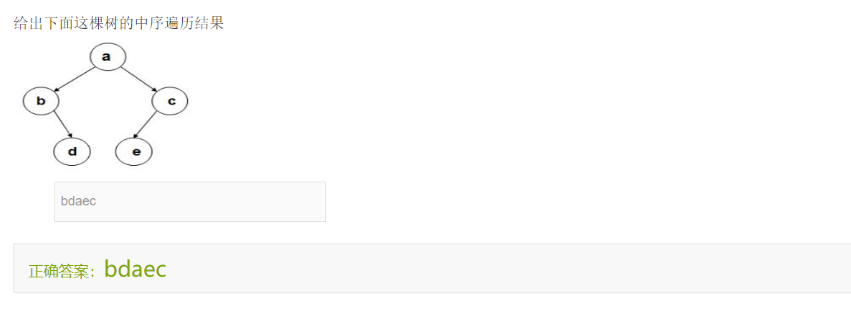
   

   

3. 后序遍历（Postorder Traversal）：先遍历左子树，再遍历右子树，最后访问根节点。

   遍历过程为：
   1.后序遍历其左子树
   2.中序遍历其右子树 
   3.访问根结点
   对应的递归程序：
   void PreOrderTraversal(BinTree BT)//BT是树
   {if( BT ){//看树是不是空的，空的就退出去，不空就访问根节点PreOrderTraversal(BT->Left);//指向左子树的那个根节点的地址进行递归PreOrderTraversal(BT->Right);//指向右子树的那个根节点的地址进行递归printf("d",BT->Data);}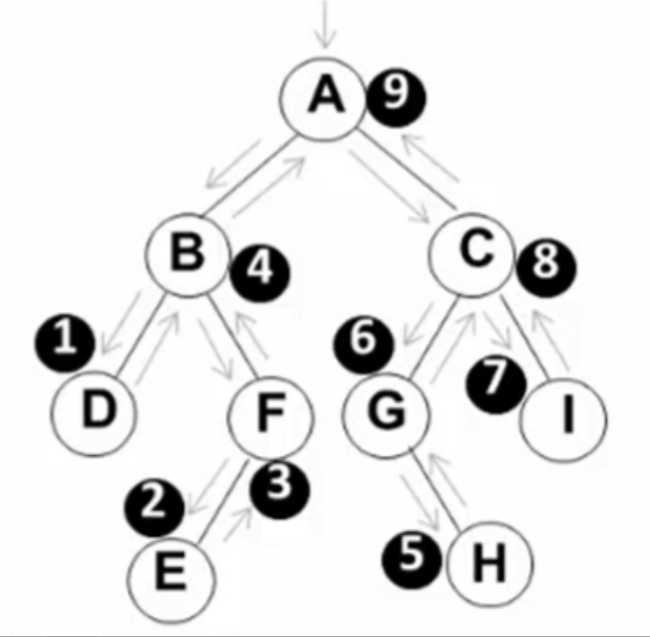
   }
   

   

   注意点：后序遍历，那当然得从下面开始咯，所以会发现B跟E是E优先。H跟C比是H优先(D E F B)(H G I C) A后序遍历 => D E F B H G I C A
   

---

3.1 先序、中序、后序遍历

• 先序遍历：根 -> 左 -> 右
• 中序遍历：左 -> 根 -> 右
• 后序遍历：左 -> 右 -> 根

先序、中序和后序遍历过程：遍历过程中经过结点的路线一样，只是访问各结点的时机不同
图中先从入口到出口的曲线上用三种符号分别标记除先序，中序和后序的访问各结点时刻

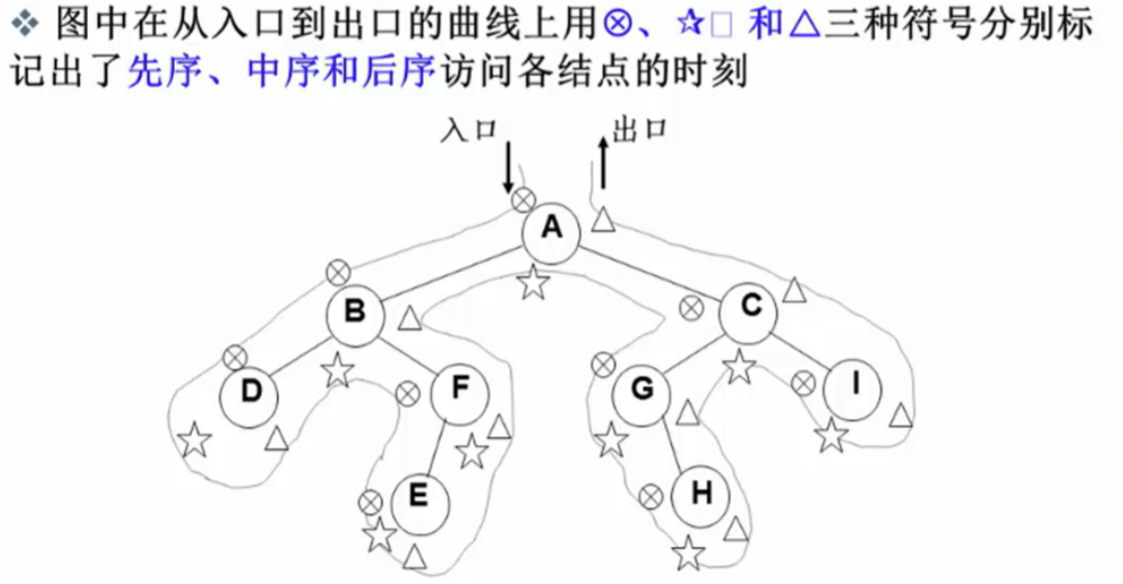
例子：

给定一个二叉树，使用先序遍历依次访问 A、B、D、E、C、F、G。

---

3.2 中序非递归遍历

中序遍历的非递归实现通常使用堆栈来模拟递归调用的过程。基本思路是：

• 先将所有左子节点压入栈中，然后依次弹出节点访问，最后处理右子树。

1.遇到一个结点，就把它压栈，并去遍历它的左子树;
2.当左子树遍历结束后，从栈顶弹出这个结点并访问它;
3.然后按其右指针再去中序遍历该结点的右子树以下是完整代码实现演示
void InOrderTraversal(BinTree BT)
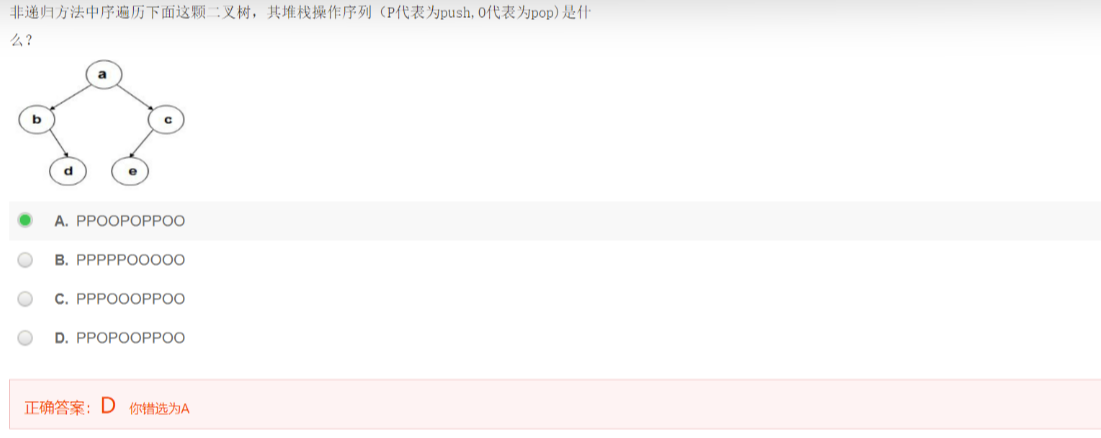
{BinTree T = BT;//把BT赋给临时变量TStack S = CreateStack(MaxSize);//创建并初始化堆栈while(T || !IsEmpty(S) ){//树不空且堆栈不空while(T){//判断堆栈空不空//一直向左并将沿途结点压入堆栈Push(S,T);//把T压入堆栈S中T = T->Left;//然后把T往左挪，就是边挪边把结点压到堆栈里面去，压到底T为NULL就退出来}if(!IsEmpty(S)){T = Pop(S);//结点弹出堆栈printf("%5d",T->Data);//(访问)打印结点T = T->Right;//转向右子树}}
}ppoopoppoo错误PPOPOOPPOO正确第二次碰到同一个的时候就print出来

先序遍历非递归算法：

只需在中序非递归遍历的基础上，将访问根节点的代码移至 Push 操作之后。

---

3.3 层序遍历

层序遍历 是按照树的层次依次访问节点的遍历方式。通常使用队列来实现，将每层节点依次入队并处理。

1.从结点访问其左、右儿子结点
2.访问左儿子后，右儿子结点怎么办？1.需要一个存储结构保存暂时不访问的结点2.存储结构：堆栈、队列

队列实现

遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点出队、访问该结点、其左右儿子入队

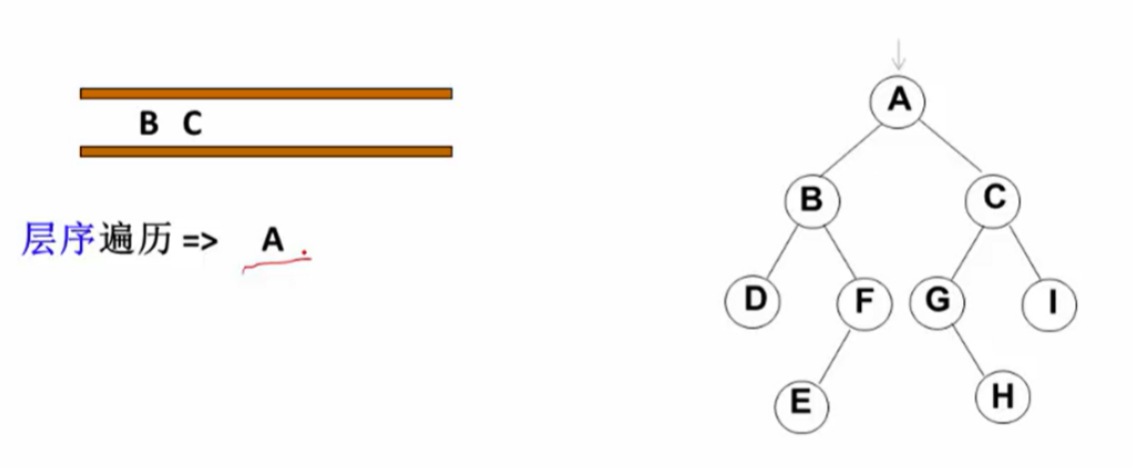
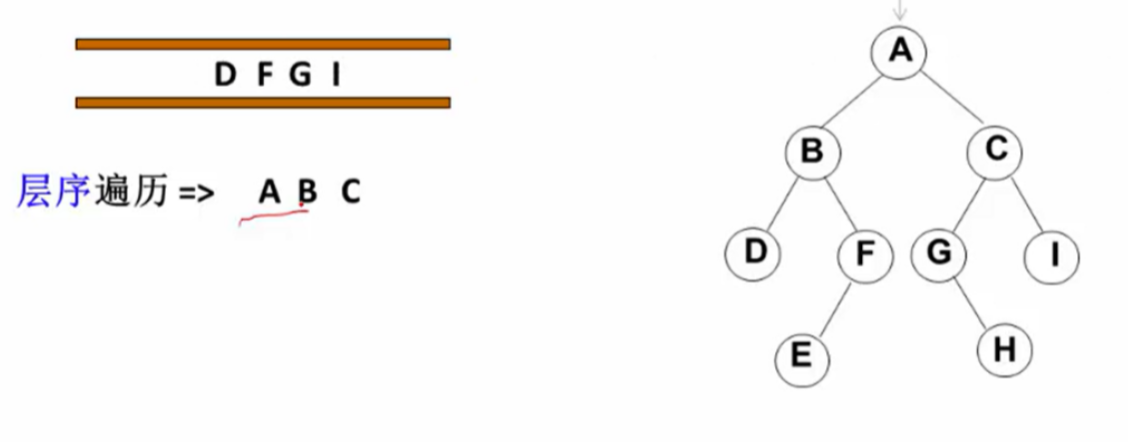
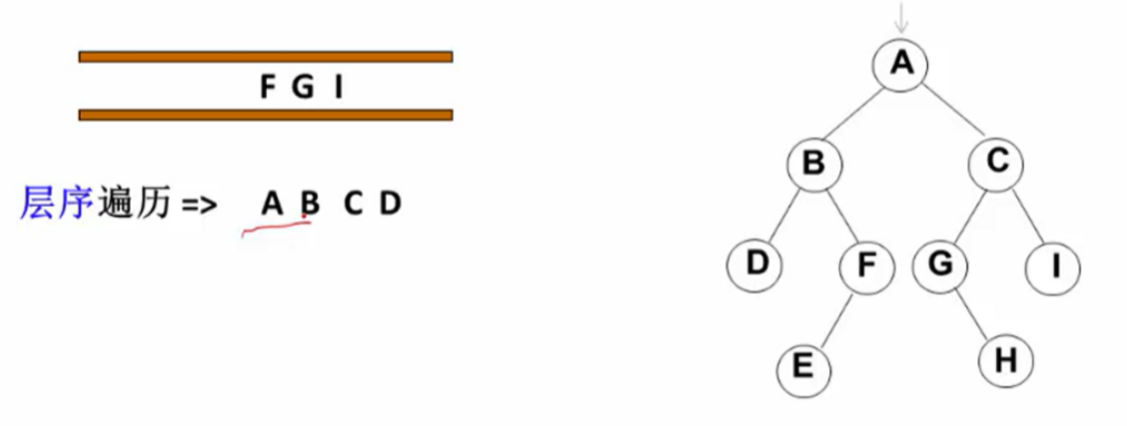
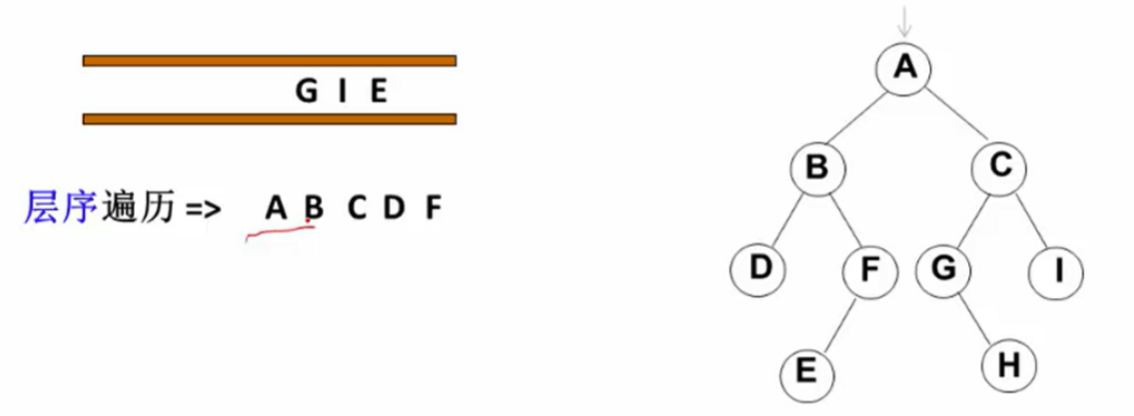
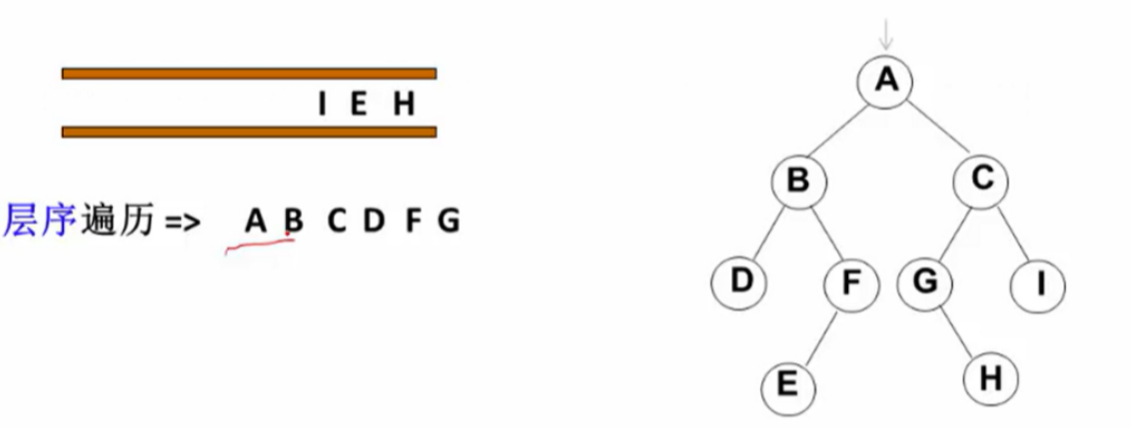
最后结果就是：层序遍历 => A B C D F G I E H

//代码实现
void LevelOrderTraversal(BinTree BT)
{Queue Q; BinTree T;if(!BT) return;//若是空树直接返回Q = CreateQueue(MaxSize);//创建并初始化队列QAddQ(Q,BT);//把BT这个根节点放到Q这个队列里while(!IsEmptyQ(Q)){T = DeleteQ(Q);//抛出元素赋给T就是一个指针printf("%d\n",T->Data);//访问去除队列的结点if(T->Left) Add(Q,T->Left);//左右儿子放到队列里去if(T->Right) AddQ(Q,T->Right);}
}

---

3.4 遍历的应用

例1：输出二叉树中的叶子节点

在遍历过程中，判断节点的左右子树是否为空，若为空则该节点为叶子节点。

void PreOrderPrintLeaves(BinTree BT)
{if(BT){if(!BT-Left && !BT->Right)printf("%d",BT->Data);PreOrderPrintLeaves(BT -> Left);PreOrderPrintLeaves(BT -> Right);}
}

例2：求二叉树的高度

二叉树的高度可以通过递归求解，根节点的高度等于其左右子树中较大高度加 1。

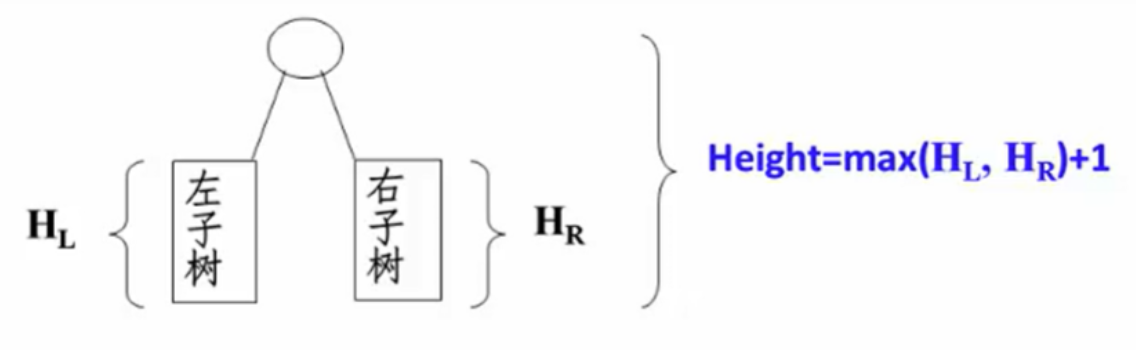
void PreOrderGetHeight(BinTree BT)
{int HL,HR,MaxHif(BT){HL = PostOrderGetHeight(BT->Left);//求左子树的深度，这两个都是递归哦HR = PostOrderGetHeight(BT->Right);//求右子树的深度MaxH = (HL > HR) ? HL :HR;//取左右子树较大的深度return (MaxH + 1);//返回树的深度}else return 0;//空树深度为0
}

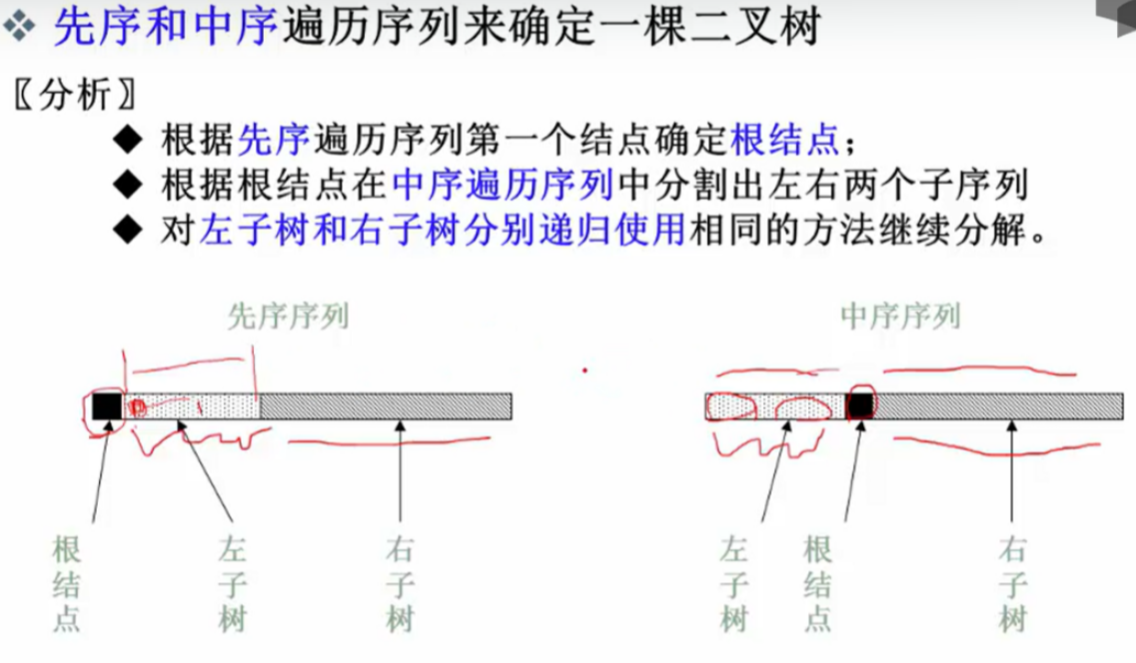
例3：由遍历序列确定二叉树

已知三种遍历中的任意两种遍历序列，能否唯一确定一颗二叉树呢？

答案：必须要有中序遍历才行

没有中序的困扰:

​ 1.先序遍历序列：A B

​ 2.后序遍历序列：B A

会发现符合条件的树不止一个

先序第一个是根，后序最后一个是根