icons8_简网app工场在线制作_搜索引擎的工作原理有哪些_优秀软文范例800字

题目描述：

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' 组成，捕获 所有 被围绕的区域：

• 连接：一个单元格与水平或垂直方向上相邻的单元格连接。
• 区域：连接所有 'O' 的单元格来形成一个区域。
• 围绕：如果您可以用 'X' 单元格 连接这个区域，并且区域中没有任何单元格位于 board 边缘，则该区域被 'X' 单元格围绕。

通过将输入矩阵 board 中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。

示例 1：

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]

输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]

解释：

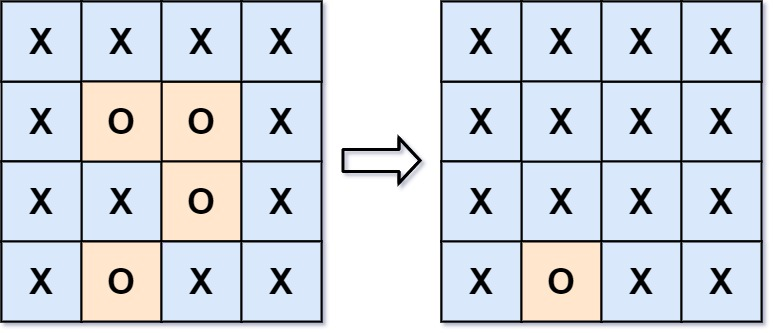
在上图中，底部的区域没有被捕获，因为它在 board 的边缘并且不能被围绕。

示例 2：

输入：board = [["X"]]

输出：[["X"]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] 为 'X' 或 'O'

题目链接：

. - 力扣（LeetCode）

解题主要思路：

这题我觉得有两个麻烦，第一个麻烦就是不好理解题目啥意思，其实题目的意思是：除了边边的 'O' 以及能跟其构成‘连接’的 'O'，其余的全部改成 'X'。第二个麻烦就是理解完题目的意思后，怎么把符合条件的区域 'O' 和 不符合条件的区域 'O' 分隔开来，其实有个办法就是，咱们遍历边边的元素，如果有不符合条件的 'O'（边边的 'O' 以及能跟其构成‘连接’的 'O'），咱们把他改成于 'O' 'X' 无关的符号，譬如 '?' ，之后二维数组内的所有 'O' 都是符合条件的 'O'（即需要改为 'X' 的），数组内的所有 '?' 都是原本不符合条件的 'O' ，我们需要将其改回来。

解题代码：

class Solution {
public:typedef pair<int, int> PII;int dx[4]{0, 0, 1, -1};int dy[4]{1, -1, 0, 0};int m, n;void solve(vector<vector<char>>& board) {m = board.size(), n = board[0].size();// 先将与边缘的‘O‘相连的全部改为’O‘、‘X’无关的符号，譬如'?'；for (int i = 0; i < n; ++i) { // 第一行和最后一行if (board[0][i] == 'O') bfs(board, 0, i );if (board[m-1][i] == 'O') bfs(board, m-1, i);}for (int j = 0; j < m; ++j) { // 第一列和最后一列if (board[j][0] == 'O') bfs(board, j, 0);if (board[j][n-1] == 'O') bfs(board, j, n-1);}// 此时二维数组board里的全部'O'全部符合题目要求，可直接改成'X'for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (board[i][j] == '?') board[i][j] = 'O';else if (board[i][j] == 'O') board[i][j] = 'X';}}}void bfs(vector<vector<char>>& board, int r, int c){queue<PII> que;que.push(make_pair(r, c));board[r][c] = '?';while (que.size()) {auto [a, b] = que.front();que.pop();for (int i = 0; i < 4; ++i) {int x = a + dx[i];int y = b + dy[i];if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O') {que.push(make_pair(x, y));board[x][y] = '?';}}}}
};