题目描述
给你一个 m x n 的整数网格图 grid ,你可以从一个格子移动到 4 个方向相邻的任意一个格子。
请你返回在网格图中从 任意 格子出发,达到 任意 格子,且路径中的数字是 严格递增 的路径数目。由于答案可能会很大,请将结果对 109 + 7 取余 后返回。
如果两条路径中访问过的格子不是完全相同的,那么它们视为两条不同的路径。
示例 1:
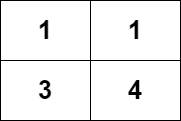
输入:grid = [[1,1],[3,4]] 输出:8 解释:严格递增路径包括: - 长度为 1 的路径:[1],[1],[3],[4] 。 - 长度为 2 的路径:[1 -> 3],[1 -> 4],[3 -> 4] 。 - 长度为 3 的路径:[1 -> 3 -> 4] 。 路径数目为 4 + 3 + 1 = 8 。
示例 2:
输入:grid = [[1],[2]] 输出:3 解释:严格递增路径包括: - 长度为 1 的路径:[1],[2] 。 - 长度为 2 的路径:[1 -> 2] 。 路径数目为 2 + 1 = 3 。
题目解析
你有一个m X n的整数网格grid,每个格子都有一个整数。你可以从一个格子移动到四个方向(上,下,左, 右)相邻的任意一个格子。要求返回网格中从任意格子出发,到任意格子,且路径中的数字是严格递增的路径数目。由于路径数目可能非常大,所以最后结果需要对109+7 取余。
严格递增路径的定义:
- 路径中的每一步,数字都必须大于前一步的数字。
解题思路
1.初始化和检查
- 初始化网络的行数和列数
- 分配并初始化用于记忆化搜索的dp数组,初始值为-1
#define MOD 100000007//定义模数,用于防止溢出int m, n;//全局变量,表示网格的行数和列数
int** dp;//用于记忆化搜索的数组
int directions[4][2] = { {0,1},{1,0},{0,-1},{-1,0} };//四个方向的移动//判断坐标(x,y)是否在网格范围
int isValid(int x, int y) {return x >= 0 && x < m && y >= 0 && y < n;
}
2.深度优先搜索(DFS)
- 使用DFS方法,从每个格子出发,计算从该格子出发的所有严格递增路径数目。
- 使用记忆化搜索,避免重复计算,提高效率。
//深度优先搜索,计算从(x,y)出发的所有路径数
int dfs(int** grid, int x, int y) {if (dp[x][y] != -1) {return dp[x][y];//如果计算过,直接返回结果}int count = 1;//起点路径长度为1//遍历四个方向for (int i = 0; i < 4; ++i){int newX = x + directions[i][0];int newY = y + directions[i][1];//判断新坐标是否有效且大于当前值if (isValid(newX, newY) && grid[newX][newY] > grid[x][y]) {count = (count + dfs(grid, newX, newY)) % MOD; // 累加路径数并取模}}dp[x][y] = count;//记忆化存储结果return count;
}
3.遍历网络
- 遍历网络的每个格子,从每个格子出发,计算总的严格递增路径数目。
//计算网格中所有递增路径的总数
int countPaths(int** grid, int gridSize, int* gridColSize) {m = gridSize;//初始化行数n = gridColSize[0];//初始化列数//分配dp数组dp = (int**)malloc(m * sizeof(int*));if (dp == NULL){fprintf(stderr, "分配 dp 数组内存失败\n");exit(EXIT_FAILURE);}for (int i = 0; i < m; ++i){dp[i] = (int*)malloc(n * sizeof(int));if (dp[i] == NULL){fprintf(stderr, "分配 dp 数组内存失败\n");exit(EXIT_FAILURE);}for (int j = 0; j < n; ++j){dp[i][j] = -1;//初始化为-1,表示未计算}}int totalPaths = 0; // 总路径数// 遍历网格的每个位置for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {totalPaths = (totalPaths + dfs(grid, i, j)) % MOD; // 累加路径数并取模}}// 释放dp数组for (int i = 0; i < m; ++i) {free(dp[i]);}free(dp);return totalPaths;
}
4.结果返回
- 最终结果对 109+710^9 + 7109+7 取余,返回总路径数目。
通过这些步骤,可以有效地计算出在网格中从任意格子出发到人一个字且路径中的数组时严格递增的路径数目。
完整代码显示
#include <stdio.h>
#include <stdlib.h>#define MOD 100000007//定义模数,用于防止溢出int m, n;//全局变量,表示网格的行数和列数
int** dp;//用于记忆化搜索的数组
int directions[4][2] = { {0,1},{1,0},{0,-1},{-1,0} };//四个方向的移动//判断坐标(x,y)是否在网格范围
int isValid(int x, int y) {return x >= 0 && x < m && y >= 0 && y < n;
}
//深度优先搜索,计算从(x,y)出发的所有路径数
int dfs(int** grid, int x, int y) {if (dp[x][y] != -1) {return dp[x][y];//如果计算过,直接返回结果}int count = 1;//起点路径长度为1//遍历四个方向for (int i = 0; i < 4; ++i){int newX = x + directions[i][0];int newY = y + directions[i][1];//判断新坐标是否有效且大于当前值if (isValid(newX, newY) && grid[newX][newY] > grid[x][y]) {count = (count + dfs(grid, newX, newY)) % MOD; // 累加路径数并取模}}dp[x][y] = count;//记忆化存储结果return count;
}
//计算网格中所有递增路径的总数
int countPaths(int** grid, int gridSize, int* gridColSize) {m = gridSize;//初始化行数n = gridColSize[0];//初始化列数//分配dp数组dp = (int**)malloc(m * sizeof(int*));if (dp == NULL){fprintf(stderr, "分配 dp 数组内存失败\n");exit(EXIT_FAILURE);}for (int i = 0; i < m; ++i){dp[i] = (int*)malloc(n * sizeof(int));if (dp[i] == NULL){fprintf(stderr, "分配 dp 数组内存失败\n");exit(EXIT_FAILURE);}for (int j = 0; j < n; ++j){dp[i][j] = -1;//初始化为-1,表示未计算}}int totalPaths = 0; // 总路径数// 遍历网格的每个位置for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {totalPaths = (totalPaths + dfs(grid, i, j)) % MOD; // 累加路径数并取模}}// 释放dp数组for (int i = 0; i < m; ++i) {free(dp[i]);}free(dp);return totalPaths;
}
int main() {// 示例输入int gridSize = 3;int gridColSize[] = { 3, 3, 3 };// 分配并初始化网格int** grid = (int**)malloc(gridSize * sizeof(int*));for (int i = 0; i < gridSize; ++i) {grid[i] = (int*)malloc(gridColSize[i] * sizeof(int));}// 填充示例数据grid[0][0] = 1, grid[0][1] = 2, grid[0][2] = 3;grid[1][0] = 6, grid[1][1] = 5, grid[1][2] = 4;grid[2][0] = 7, grid[2][1] = 8, grid[2][2] = 9;// 计算路径总数int totalPaths = countPaths(grid, gridSize, gridColSize);printf("总路径数: %d\n", totalPaths);// 释放grid数组for (int i = 0; i < gridSize; ++i) {free(grid[i]);}free(grid);return 0;
}













