统计信号处理基础 习题解答11-2

题目

对于后验PDF

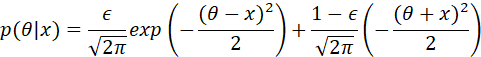
画出和时的PDF。然后，对于同样的值,求 MMSE和 MAP 的估计量。

---

解答

根据题目条件，通过Matlab，画出两个函数的概率密度函数图像，其中的x设定为2.

clc, clear, close all;
x=2;
e=0.5;
theat=-10:0.01:10;
p_theat=e/sqrt(2*pi)*exp(-0.5*(theat-x).^2)+(1-e)/sqrt(2*pi)*exp(-0.5*(theat+x).^2);
figure(1)
plot(theat,p_theat)
hold on
xline(x);
xline(-x)
hold offe=0.75;
p_theat=e/sqrt(2*pi)*exp(-0.5*(theat-x).^2)+(1-e)/sqrt(2*pi)*exp(-0.5*(theat+x).^2);
figure(2)
plot(theat,p_theat)
hold on
xline(x);
xline(-x)
hold off

---

时，做出图案：

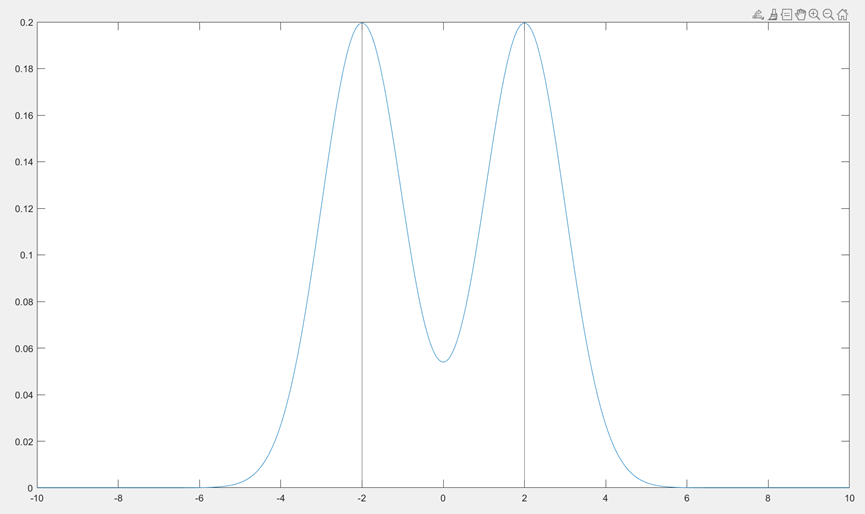
此时可以发现，是个偶函数，因此：

也就是此时的的MMSE估计量为0。

而对的观察可知，该函数存在两个极值点，所以的MMSE估计量不唯一：

 

---

当时

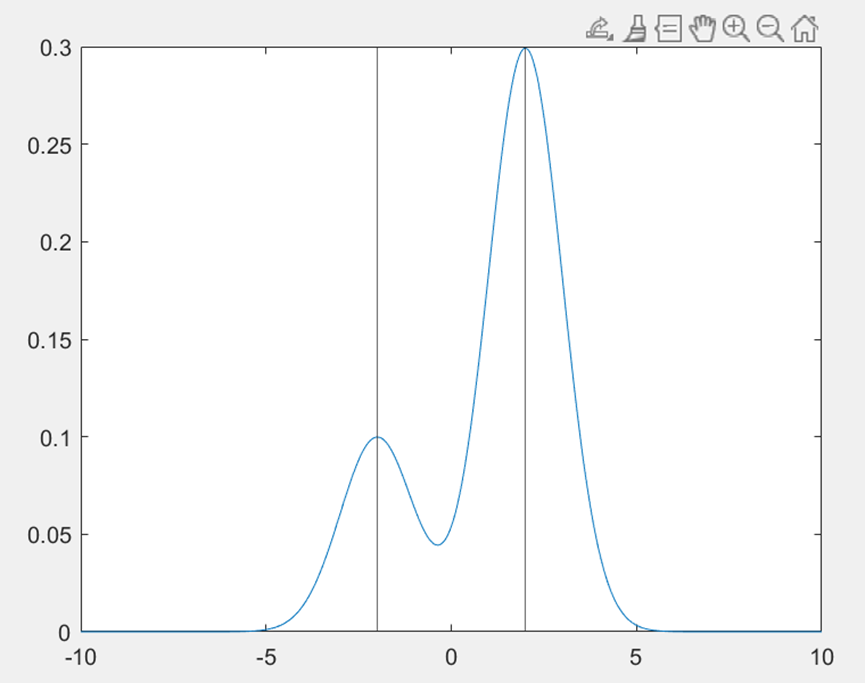
计算MMSE：

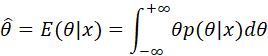
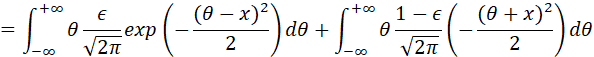
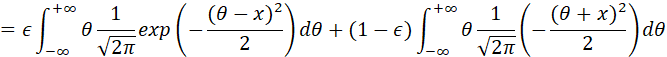
上式的积分，分别是和的数学期望，因此可以得到：

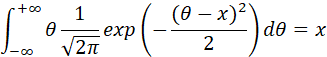
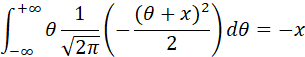
因此：当时

此时代入也验证了上半题目的结论。

而观察图像的特性，可以发现该函数存在一个极值点，也就是的MAP估计量为：

经过这个例子分析，可以发现，MAP估计量不一定等于MMSE估计量。

书上举得联合分布是高斯，先验也是高斯情况下两者相等，只是特例。