常见排序算法之快速排序

目录

一、什么是快速排序

二、代码实现

2.1 hoare版本

2.1.1 思路

2.1.2 C语言源码

2.2 挖坑法

2.2.1 思路

2.2.2 C语言源码

2.3 前后指针版本

2.3.1 思路

2.3.2 C语言源码

​编辑

三、效率优化

3.0 时间复杂度分析

3.1 三数取中法

3.2 小区间优化

四、非递归写法

4.1 思路

4.2 C语言源码

---

一、什么是快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。

它的基本思想为：

1. 任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值。
2. 然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

二、代码实现

2.1 hoare版本

2.1.1 思路

采取先部分后整体的思路进行讲解

• 考虑单次

1. 右指针先去找比基准值小的的位置
2. 左指针去找比基准值大的位置
3. 两个位置进行交换
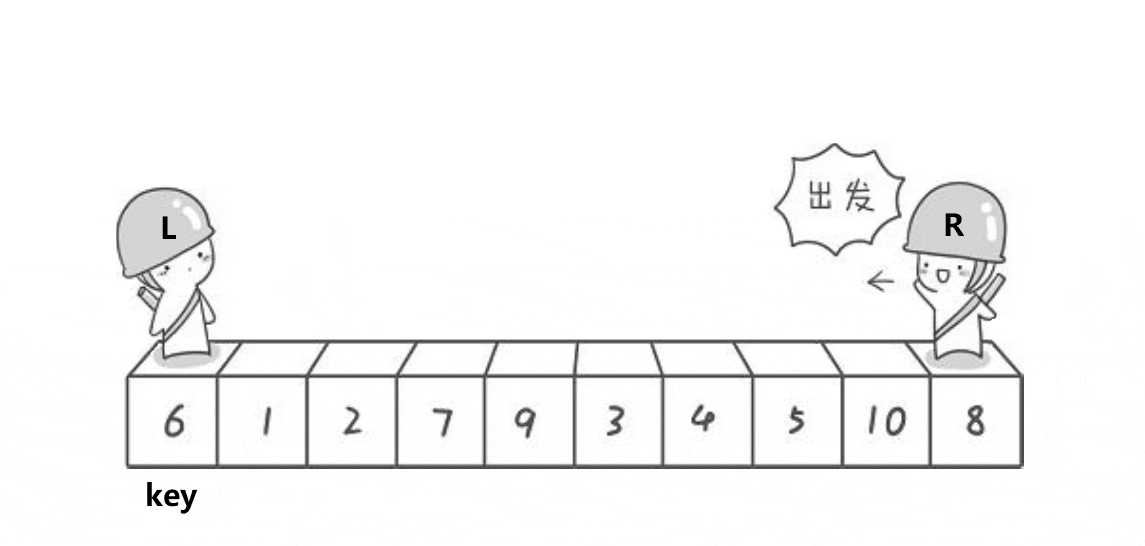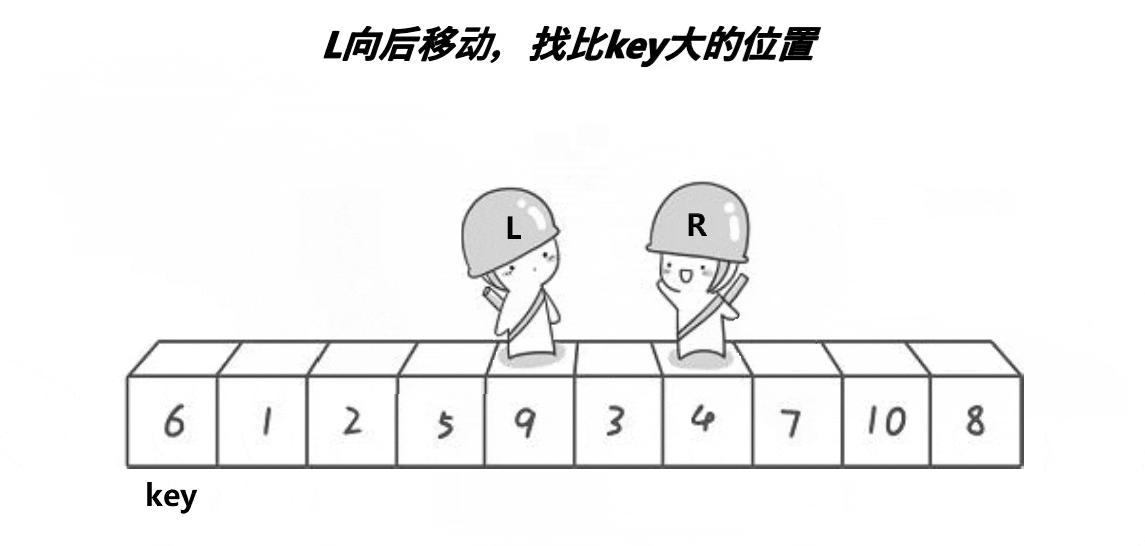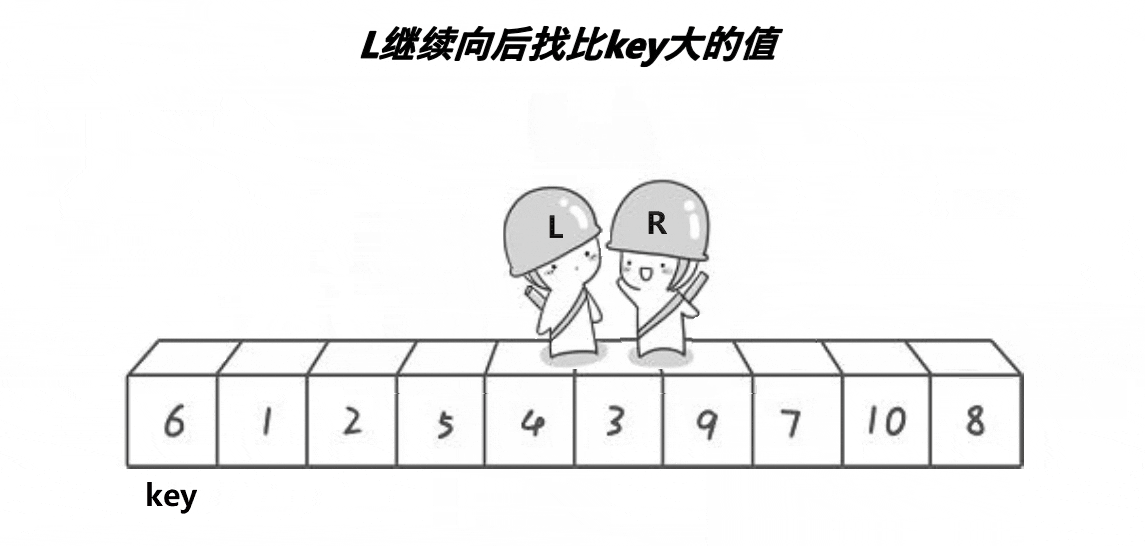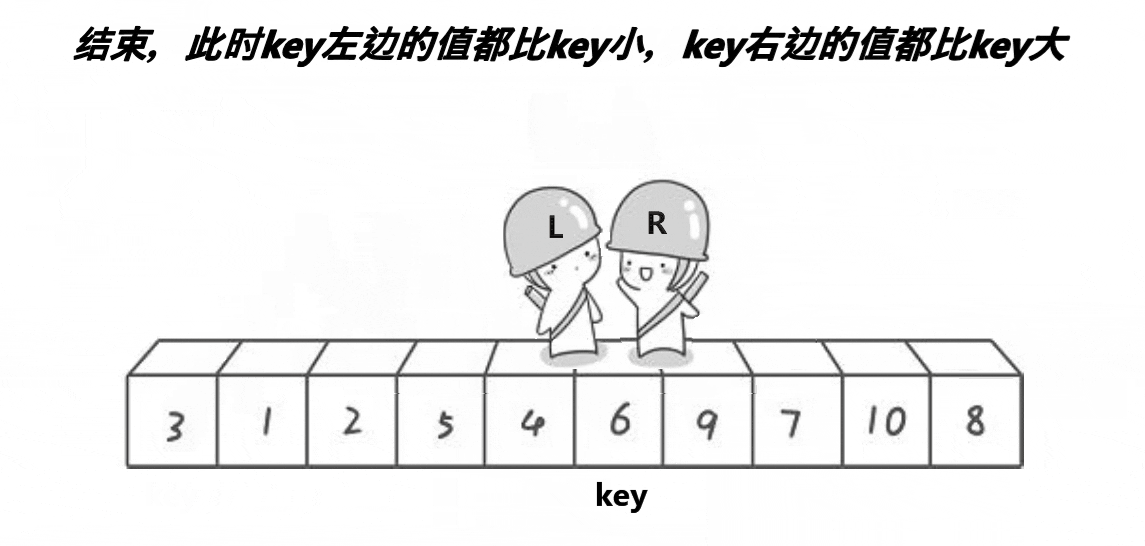
4. 重复上述过程，直到左指针等于右指针。此时实现了相遇位置左边的值都小于基准值，右边的值都大于基准值。
5. 按照基本思想，将此相遇位置与基准值进行交换。就完成了单趟排序

• 考虑整体

1. 采用类似二分法的思路，不断分成小的区间
2. 停止二分的条件是：左右区间重合（即左区间的值等于右区间）或者 区间不存在（即左区间的值大于右区间）
3. 每次递归传值：右区间为[起始位置，相遇位置的前一个位置]；左区间为[相遇位置的后一个位置，结束位置]

2.1.2 C语言源码

void Hoare(int* a, int left, int right)
{//递归结束条件if (left >= right){return;}int begin = left;int end = right;//单趟while (begin < end){//先右取小while (begin < end && a[end] > a[left]){end--;}//后左取大while (begin < end && a[begin] <= a[left]){begin++;}//交换Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[left]);//递归//左区间Hoare(a, left, begin - 1);//右区间Hoare(a, begin + 1, right);
}

2.2 挖坑法

2.2.1 思路

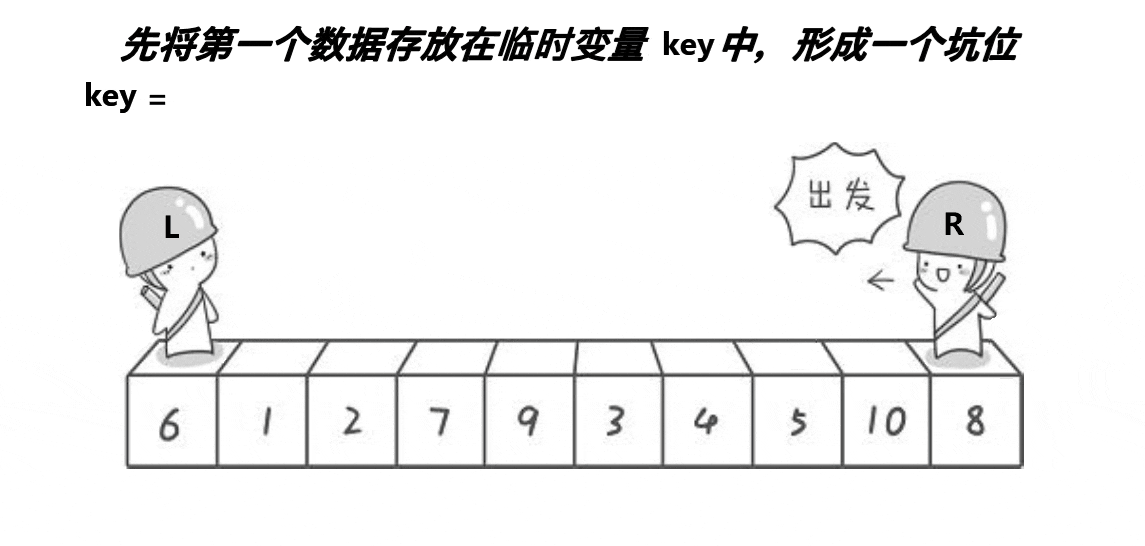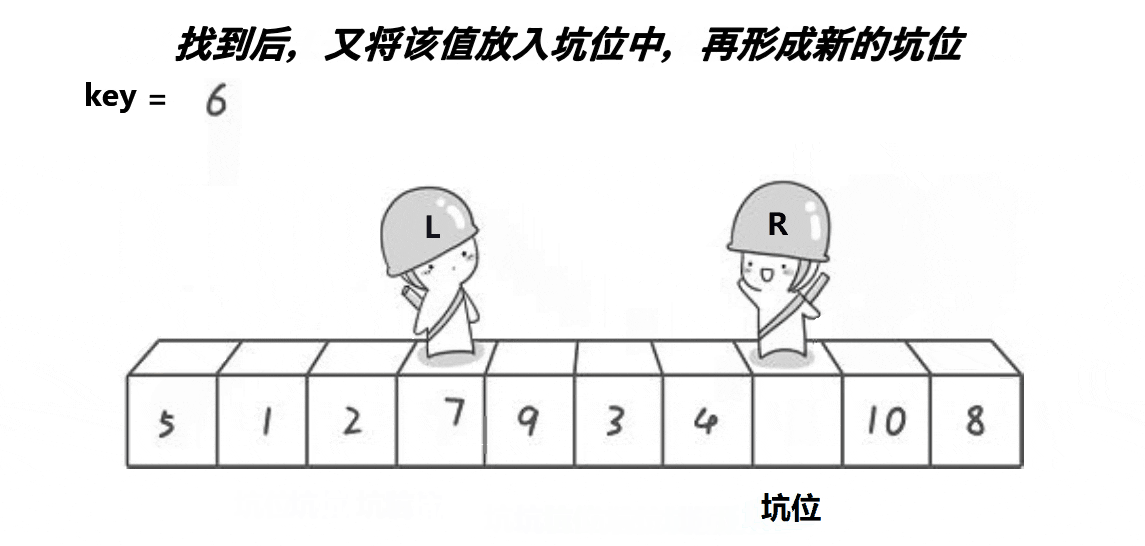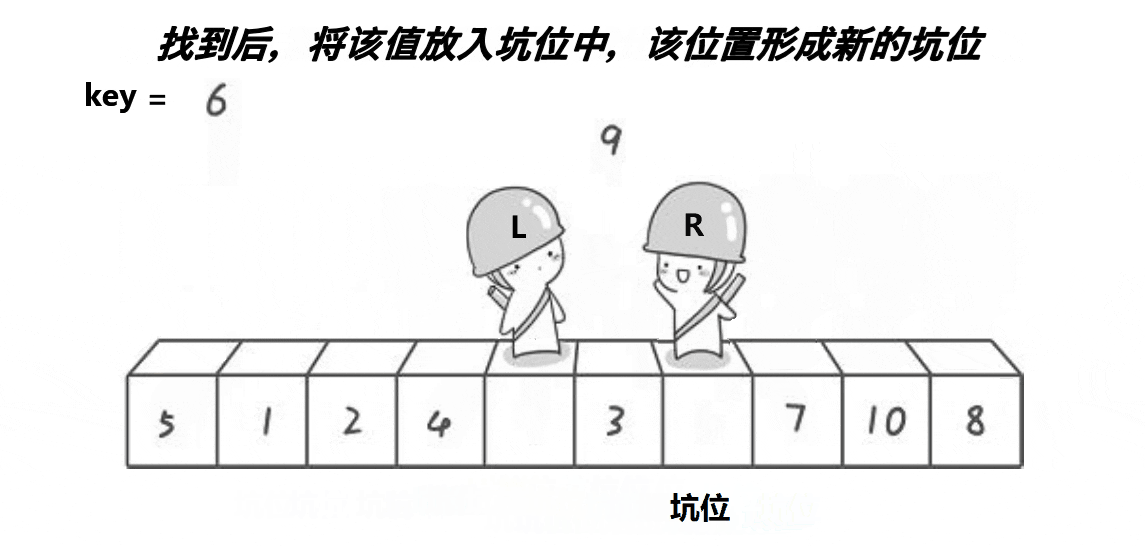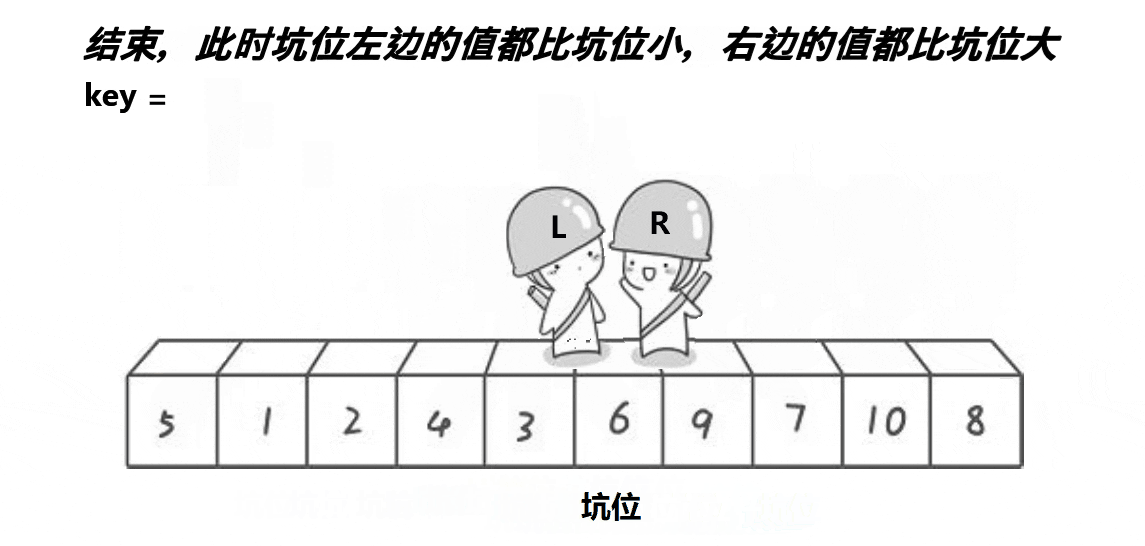
挖坑法提出的目的是解决Hoare版本不易于理解的问题，算法效率上没有任何提升。

• 考虑单次：

1. 将基准值存起来。
2. 右指针找小，放入原先坑位，形成新的坑位。
3. 左指针找大，放入原先坑位，形成新的坑位。
4. 最后将相遇位置的坑位放入基准值

• 考虑整体：

1. 与Hoare版本递归思路如出一辙，不再进行详细讲解

2.2.2 C语言源码

void DigHole(int* a, int left, int right)
{if (left >= right){return;}int key = a[left];int begin = left;int end = right;while (begin < end){//先从右找出比key小的值while (begin < end && a[end] > key){end--;}//放到坑位上a[begin] = a[end];//再从左找出比key大的值while (begin < end && a[begin] <= key){begin++;}//放到坑位上a[end] = a[begin];}a[begin] = key;//左区间DigHole(a, left, begin - 1);//右区间DigHole(a, begin + 1, right);
}

2.3 前后指针版本

2.3.1 思路

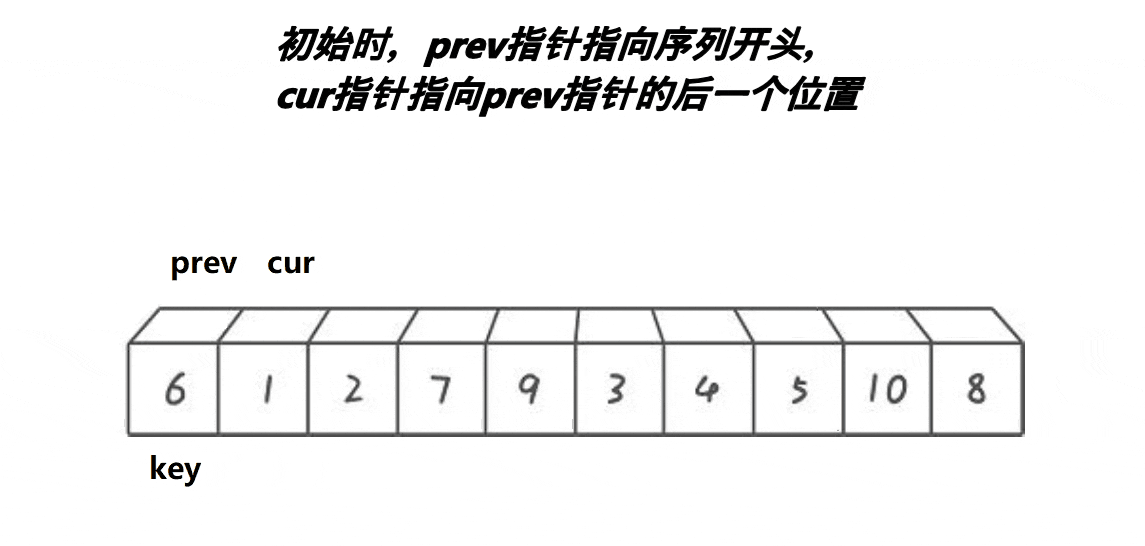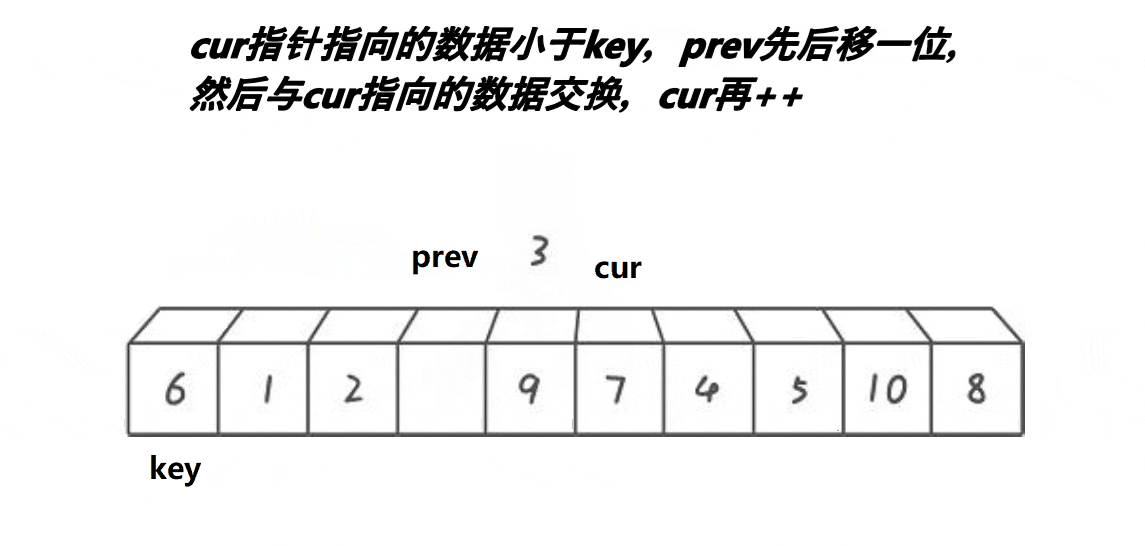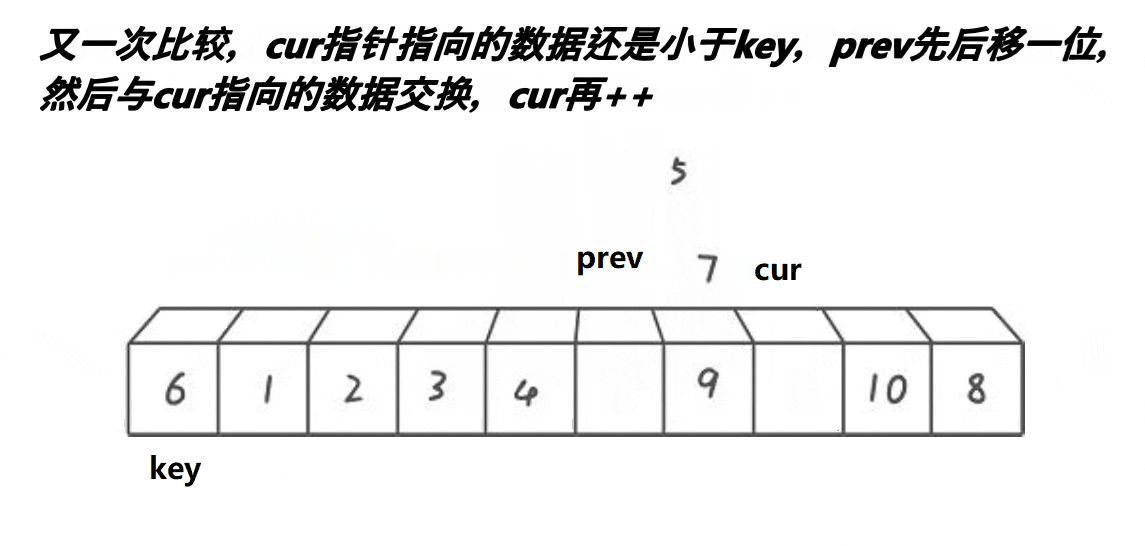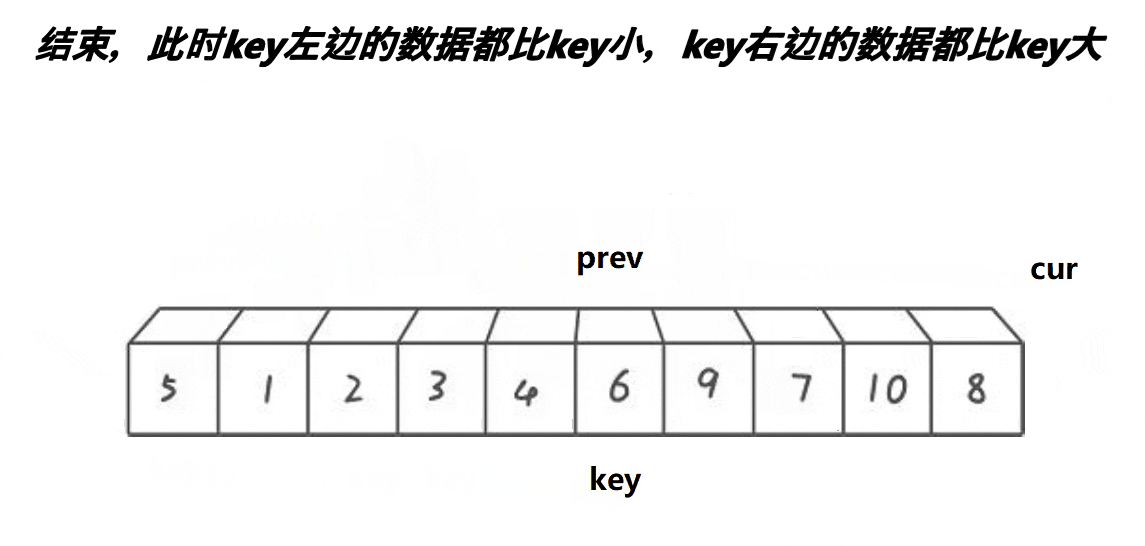
前后指针版本大大节约了代码量，是推荐的快速排序实现的版本

• 考虑单次：

1. prev指针指向起始位置，cur指针指向prev的下一个位置
2. 如果cur指向的值小于基准值，1.prev先向前移动 2.然后与cur指针指向的位置交换 3.最后cur指针移动到下一个位置（实际上没有进行交换，仅仅是cur指针与prev指针一起移动到下一个位置）
3. 如果cur指针指向的值大于基准值，cur指针一直移动直到找到比基准值小的位置为止。将此位置与prev指针指向的下一个位置交换。
4. 最后将prev指向的位置与基准值位置交换
5. 结束条件是cur指针越界

• 考虑整体： 

1. 与Hoare版本递归思路如出一辙，不再进行详细讲解

2.3.2 C语言源码

void DoublePoint(int* a, int left, int right)
{if (left >= right){return;}int prev = left;int cur = left + 1;int keyi = left;while (cur <= right){if (a[cur]<a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[keyi], &a[prev]);keyi = prev;//左区间DoublePoint(a, left, keyi - 1);//右区间DoublePoint(a, keyi + 1, right);
}

三、效率优化

3.0 时间复杂度分析

一般情况下的时间复杂度类似于二叉树的时间复杂度计算为 O(nlogn)

最坏的情况下，即为给定数组本身是有序的，仍然需要分区间来交换。此时的情况类比于极端的单叉树，时间复杂度为O(n^2)

所以基准值的选择是提高快速排序效率的关键，下述的三数取中法就是解决方法之一

3.1 三数取中法

每次取出区间端点以及区间中点的值比较，取中间值，这样就可以规避上述问题

int GetMidi(int* a, int left, int right)
{int midi = (left + right) / 2;int maxi = 0;if (a[left] < a[midi]){if (a[midi] < a[right]){return midi;}else if(a[left] < a[right]){return right;}else{return left;}}else{if (a[midi] > a[right]){return midi;}else if (a[left] < a[right]){return left;}else{return right;}}
}

3.2 小区间优化

综合选取一个时间复杂度、空间复杂度较小且稳定性高的排序——插入排序

具体讲解请点击：常见排序算法之插入排序-CSDN博客

四、非递归写法

递归需要创建栈帧，极端情况下可能会导致栈溢出。所以采用模拟递归版本实现快速排序是非常必要的

4.1 思路

快速排序采用递归的本质目的是存储了每次排序的区间，递归到最小区间然后逐层解决问题。很明显栈的先进后出的特性满足我们的需求。

栈的源码及详解请点击：数据结构之栈-CSDN博客

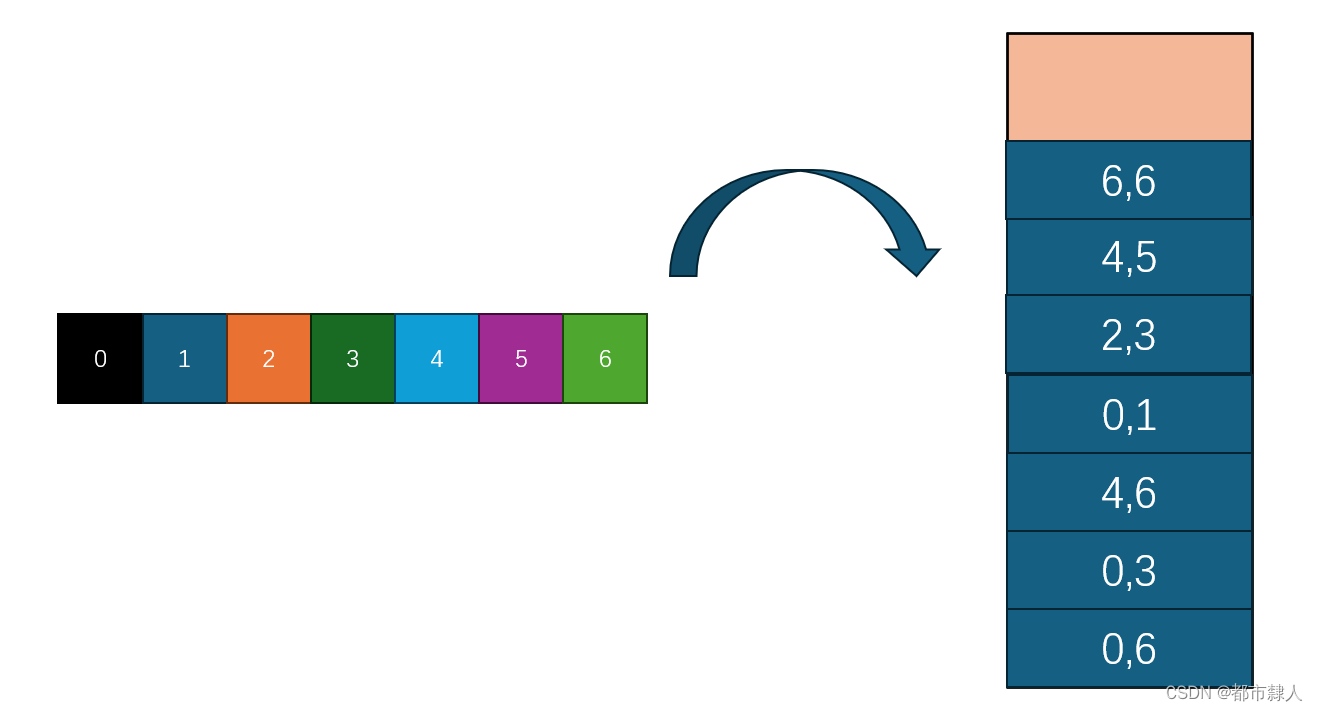
• 考虑单次

1. 左右区间入栈
2. 左右区间出栈
3. 采用上述三个版本中的一个进行单趟排序（下述代码采用了双指针版本）

• 考虑循环 

1. 满足成为一个区间的条件（即左端点小于右端点），继续将左右区间入栈
2. 先处理左区间，再处理右区间
3. 循环结束条件为：栈内没有元素——即所有区间都处理完毕

4.2 C语言源码

void QuickSort(int* a, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (STEmpty(&st)==false){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);//单趟int prev = begin;int cur = begin + 1;int keyi = begin;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[keyi], &a[prev]);keyi = prev;//模拟递归//左区间if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi+1);}//右区间if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}STDestroy(&st);
}