推导和短语
推导
推导过程中,每一步推导都是对句型的 最右非终结符 进行替换,最右推导(规范推导);
短语

用 β 替换 A,则 β 就是 关于A 的一个短语;
直接短语是短语范围内的一步推导;
直接短语可能不唯一,但 最左直接短语 唯一确定,被称为句柄;
例:通过推导过程找出短语和句柄

素短语
找素短语的方法有:
找短语中最短的判断是否有终结符,若有则该短语是素短语;然后判断其他短语有是否有该素短语,若有,则其他短语不是素短语,若没有,则进一步判断是否有终结符,若有,则是,反之则不是;
以上例题中,a 和 Sb 是素短语;
语法树
基本特点和定义
1)根结点是文法开始符号;
2)内部结点一定是非终结符;
3)若某结点为ε,则该结点是叶子结点,并且其父结点无其他子结点;
根据一棵语法树无法判断是 最右推导 还是 最左推导;
短语:每个子树的叶子结点组成的符号串;
直接短语:简单子树(单层分支的子树)的 叶子结点 组成的字符串是相对于简单子树根的直接短语
句柄:最左简单子树的 叶子结点组成的字符串
素短语:子树的叶子节点组成的字符串包含终结符,且在子树中不再有包含终结符的最小子树
证明某文法二义性?
找出二义性的句子 / 句型(若某个句子能够找到两种不同的最左/右推导或者存在两棵不同的语法树)
自顶向下的语法分析
1.不确定的自顶向下语法分析
根据多个公共因子的候选式进行不确定的试探,出现错误会回溯,效率低
2.确定的自顶向下语法分析--消除左递归 消除回溯
1) 递归下降分析法;
2)LL(1)分析法;
消除左递归(直接左递归)
消除间接左递归
回溯
候选式中存在公共的左因子;
A → δβ1 | δβ2 | … | δβi | βi+1 | … | βj 消除回溯,经过反复提取左因子,就能把每个非终结符(包括新引进者)的所有候选首字符集变为两两不相交(即不含公共左因子):
递归下降分析器
要求:消除左递归; 消除回溯;
LL(1) 分析法
L : 自顶向下分析是从左向右扫描字符串的;
L : 分析过程用最左推导;
(1): 只需要向右查看一个符号就可决定如何推导;
LL(1)分析器是由 LL(1)分析表、分析栈和一个控制程序组成;
分析栈要求逆序入栈;
First集合是 针对第一个位置的终结符 ; 并且是针对产生式的左端非终结符考察的;
Follow集合是针对产生式的右端非终结符考察的;
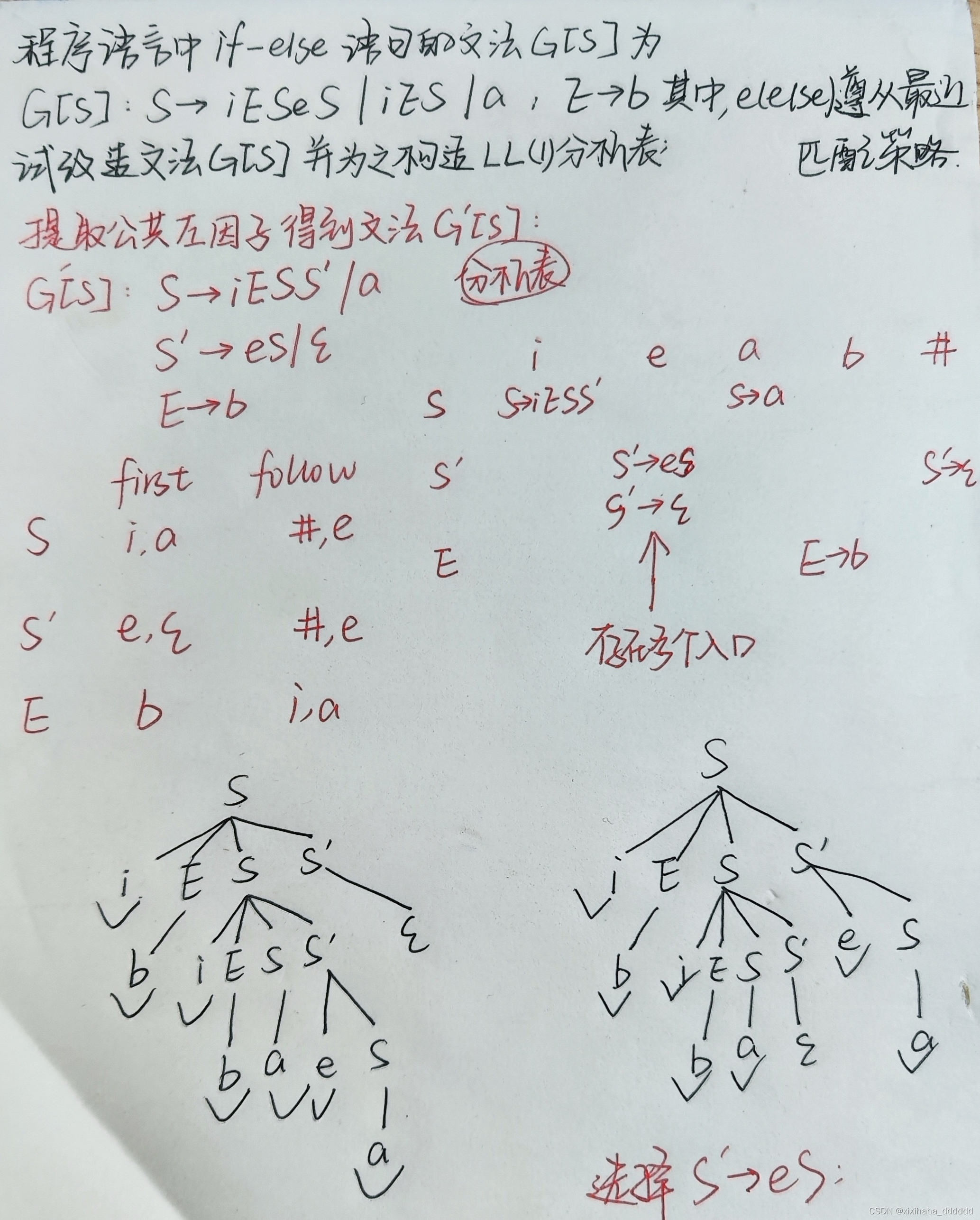
例1:

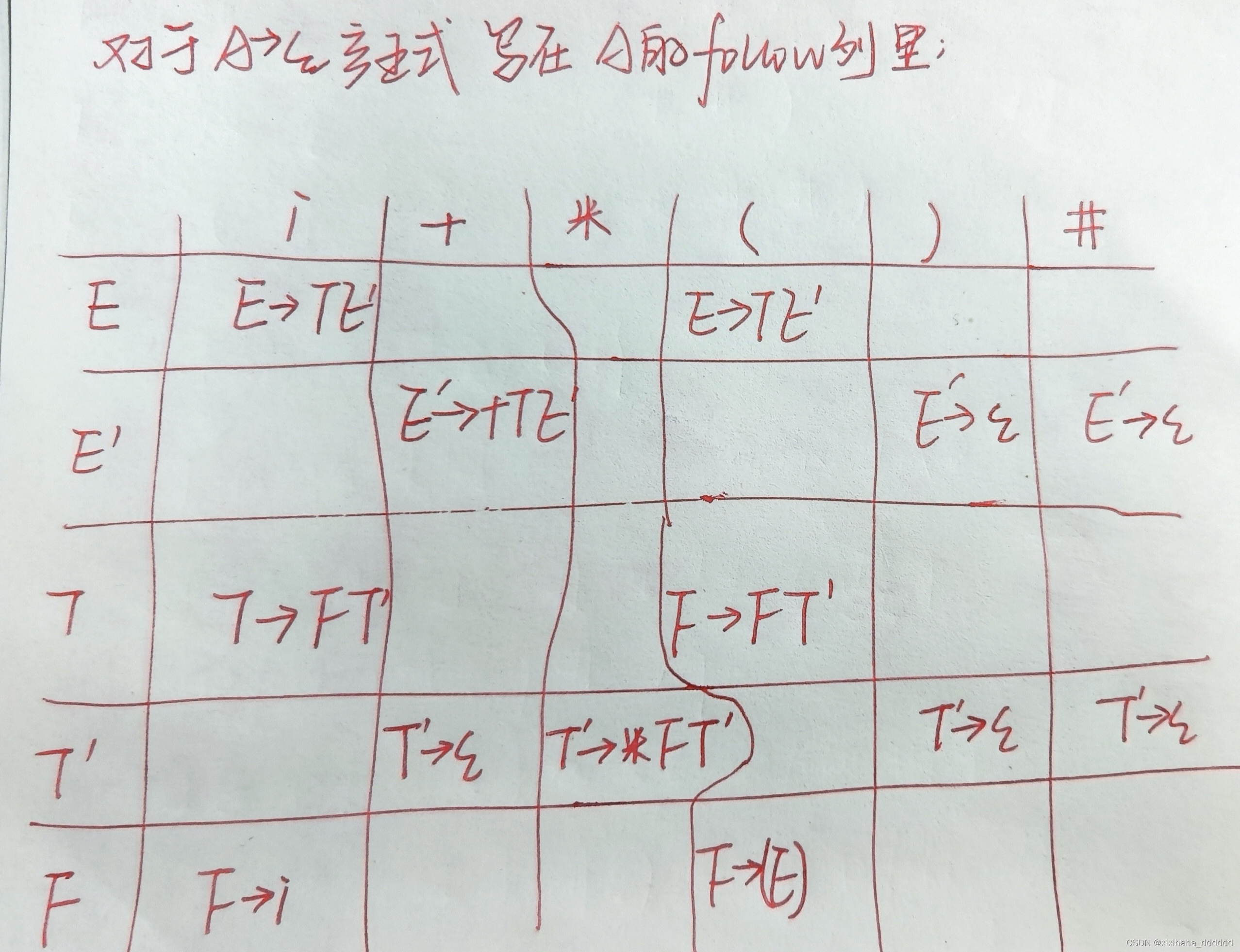

例2:修正等价的LL(1)文法

注:S的 first 集只有 i 而无分号
例3: