石家庄市官方网站_seo网站排名推广_seo秘籍优化课程_一个完整的营销策划方案范文

思路

1. dp数组定义：完全背包，不限物品使用次数，使用0-i的硬币，总和小于等于j的组合方式有dp[i][j]个
2. 递推公式：

   if(j >= coins[i])   dp[i][j] = dp[i-1][j] + dp[i][j - coins[i]];
   elsedp[i][j] = dp[i-1][j];

3. dp数组初始化：第一行以及第一列初始化为1
4. 遍历顺序：左右，上下
5. 时间复杂度：     

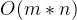
代码

class Solution {
public:int change(int amount, vector<int>& coins) {int m = coins.size();vector< vector<unsigned long long>> dp(m, vector<unsigned long long>(amount + 1, 0));if(coins[0] <= amount) dp[0][coins[0]] = 1;for (int j = coins[0] + 1; j <= amount; j++) {dp[0][j] = dp[0][j - coins[0]];}for (int i = 0; i < m; i++) {dp[i][0] = 1;}for(int i = 1; i < m; i++){for(int j = 0; j <= amount; j++){if(j >= coins[i])   dp[i][j] = dp[i-1][j] + dp[i][j - coins[i]];elsedp[i][j] = dp[i-1][j];}}return dp[m-1][amount];}
};