目录
1 主要内容
变分模态分解法
VMD-CNN-LSTM负荷预测
2 部分代码
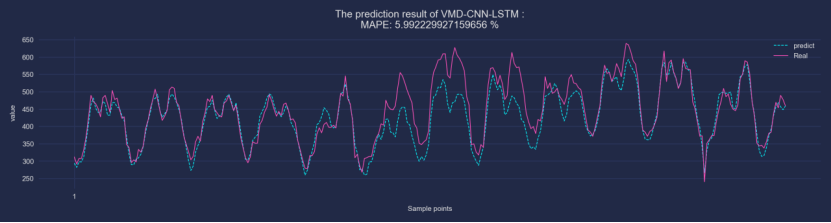
3 运行结果
4 下载链接
1 主要内容
该程序实现一种基于变分模态分解的短期电力预测模型——VMD-CNN-LSTM 模型。该模型利用 VMD 技术对原始电力负荷数据及其相关特征进行分解,并通过全连接层来输出预测结果,这种方法精度较高,可有效应对电力负荷数据的非平稳性和非线性引起的预测误差,主要原理是通过将负荷数据分解为多个相对平稳的子序列,并与其他影响因素重构特征矩阵,再使用模型重新训练,从而提升预测精度。该程序采用python编写,注释清楚,运行稳定,出图效果好!
-
变分模态分解法
在 2014 年,Konstantin Dragomiretski 和 Dominique Zosso 提出了一种用于信号分解技术的新方法——变分模态分解法(Variational mode decomposition,VMD)。这种方法是非递归的,采用自适应的变分框架来分解信号。VMD 与传统的信号分解技术相比,其分解后的子序列在保留了原始数据序列趋势特征的同时,也能有效避免了“模态混叠”对预测模型的干扰,且在处理噪声较大的信号时表现出更好的分解性能和更强的鲁棒性。
VMD 分解原始数据的步骤如下:
Step1. 针对每个模态序列,使用希尔伯特变换计算与每个模态序列相关的分析信号,以此来获取单边频谱信号。
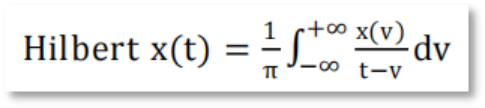
Step2. 通过向每个子序列新增指数项来对中心频率进行调整,并将子序列的频谱信号移动至基带。
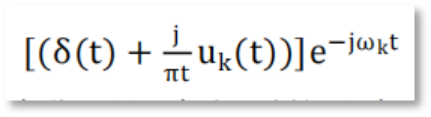
Step3. 通过解调信号的高斯平滑度得到的约束变分表达式。
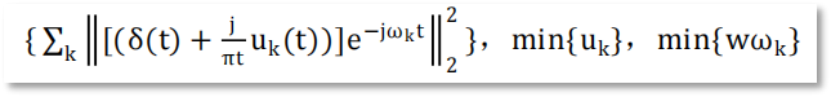
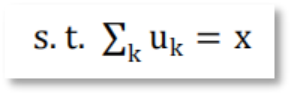

Step4. 为了将上述两个公式转化成无约束的求解式,引入二次惩罚项α和拉格朗日惩罚算子λ,得到增广拉格朗日表达式。
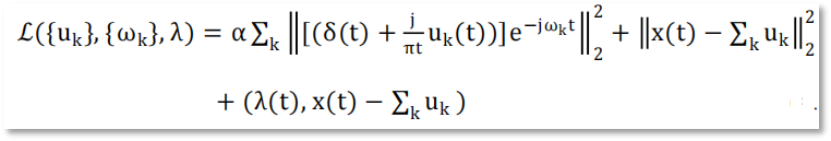
Step5. 利用乘数的交替方向法寻找增广拉格朗日表达式的鞍点,得到各模态序列的频域更新。
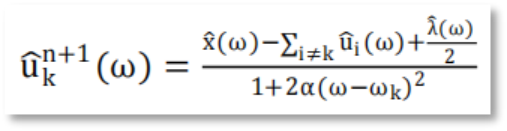
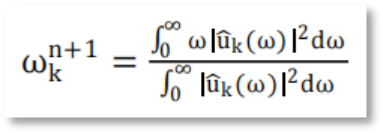
式中,n 表示迭代次数。
拉格朗日乘法算子λ需要满足下式。
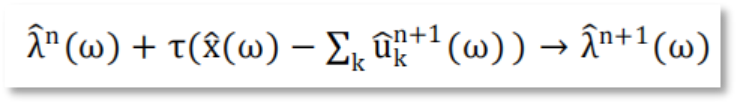
Step6. 循环求解增广拉格朗日表达式鞍点,直到模态分量满足:
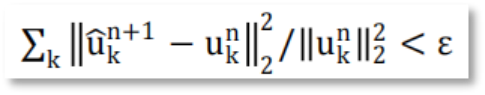
式中,ε是一个常量,决定了分解的精度和迭代次数。
-
VMD-CNN-LSTM负荷预测
首先通过 VMD 分解原始电力负荷数据序列,得到 8个平滑稳定的 IMF 子序列,在一定程度上解决了原始数据带来的非线性问题。其次分别将 8 个子序列与温度和时间等特征进行合并,构建特征矩阵,并进行归一化处理。之后将处理好的8个特征矩阵输入CNN-LSTM 模型中进行训练,输出8个子序列的预测值;最后将8个预测子序列进行叠加重构,输出最终的电力负荷预测结果。
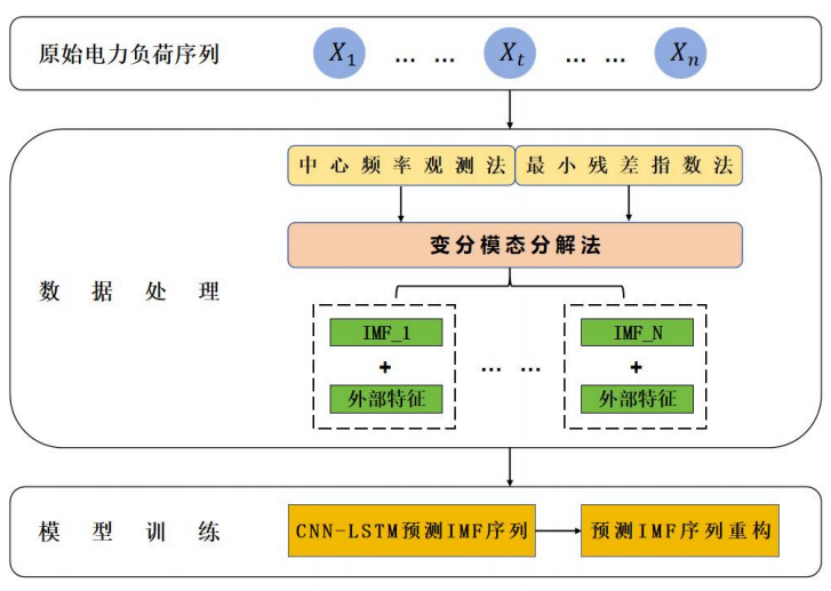
2 部分代码
for i in range(n_out):# 遍历每一个预测步长。每一列代表一步预测,现在是在求每步预测的指标actual = [float(row[i]) for row in Ytest] #一列列提取# 从测试集中提取实际值。predicted = [float(row[i]) for row in predicted_data]# 从预测结果中提取预测值。mse = mean_squared_error(actual, predicted)# 计算均方误差(MSE)。mse_dic.append(mse)rmse = sqrt(mean_squared_error(actual, predicted))# 计算均方根误差(RMSE)。rmse_dic.append(rmse)mae = mean_absolute_error(actual, predicted)# 计算平均绝对误差(MAE)。mae_dic.append(mae)MApe = mape(actual, predicted)# 计算平均绝对百分比误差(MAPE)。mape_dic.append(MApe)r2 = r2_score(actual, predicted)# 计算R平方值(R2)。r2_dic.append(r2)if n_out == 1:strr = '预测结果指标:'else:strr = '第'+ str(i + 1)+'步预测结果指标:'table.add_row([strr, mse, rmse, mae, str(MApe)+'%', str(r2*100)+'%'])return mse_dic,rmse_dic, mae_dic, mape_dic, r2_dic, table
# 显示图形。
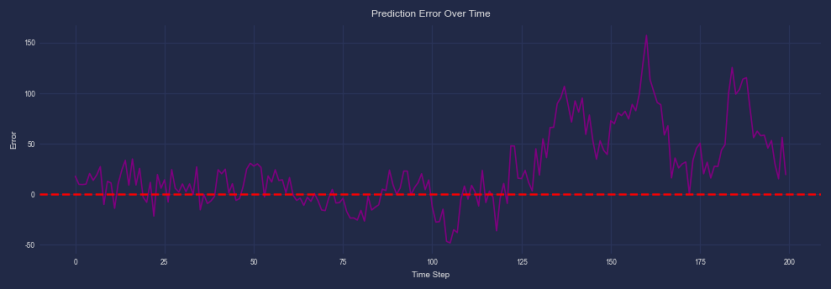
residuals = actual_test - pre_test
plt.figure(figsize=(6,4), dpi=120)
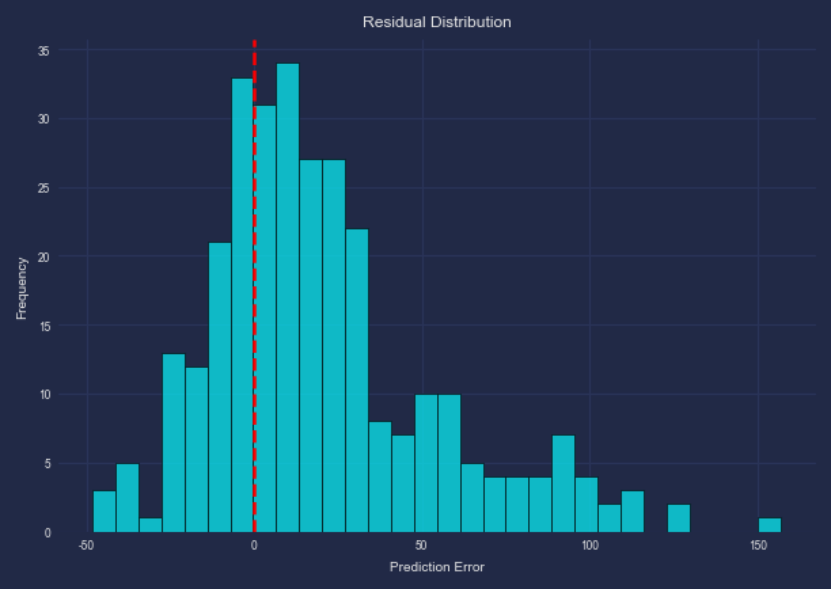
plt.hist(residuals, bins=30, edgecolor='k', alpha=0.7)
plt.title('Residual Distribution')
plt.xlabel('Prediction Error')
plt.ylabel('Frequency')
plt.axvline(x=0, color='r', linestyle='--')
plt.show()
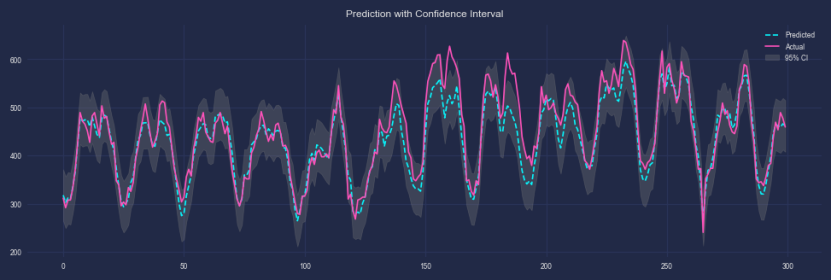
plt.figure(figsize=(10,3), dpi=120)
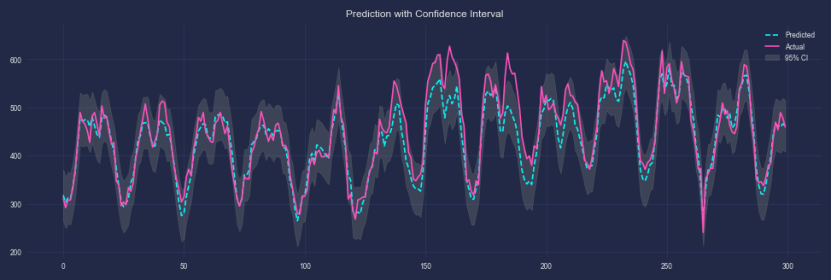
plt.fill_between(range(len(pre_test)), pre_test[:,0] - 1.96*np.std(residuals),pre_test[:,0] + 1.96*np.std(residuals),alpha=0.3, color='gray', label='95% CI')
plt.plot(pre_test[:,0], '--', linewidth=1, label='Predicted')
plt.plot(actual_test[:,0], '-', linewidth=1, label='Actual')
plt.title('Prediction with Confidence Interval')
plt.legend()
plt.show()3 运行结果